70000 / 12
interactiveleap
Sep 16, 2025 · 6 min read
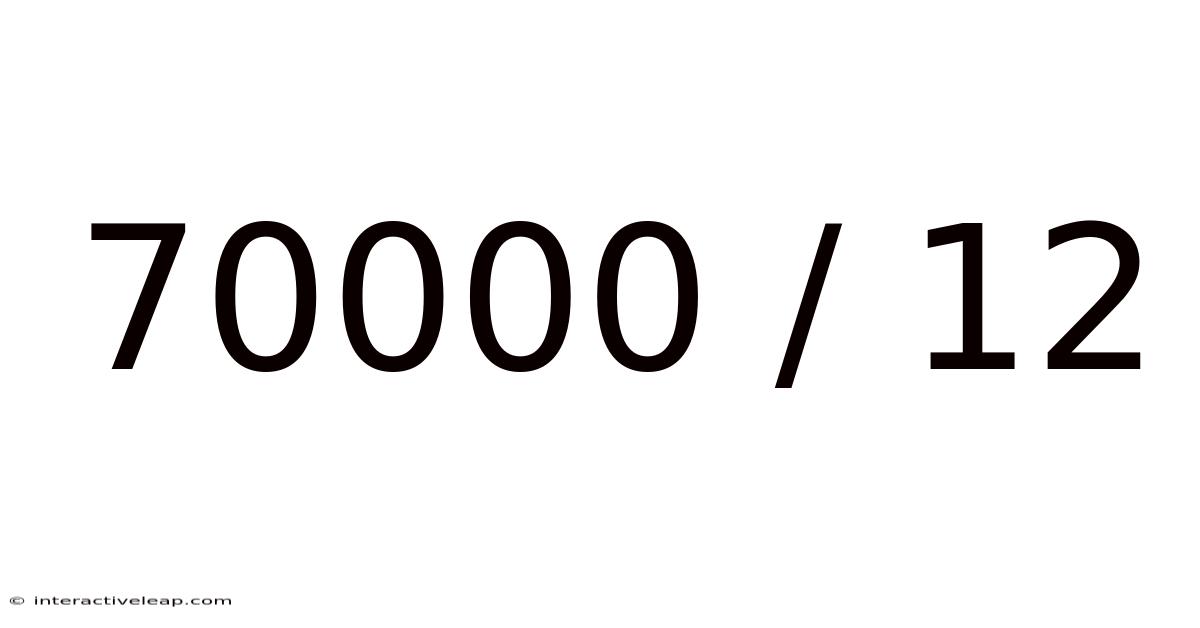
Table of Contents
Decoding 70000 / 12: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 70000 divided by 12, delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and related concepts. Understanding this division problem goes far beyond simply finding a quotient; it's a gateway to appreciating the power and versatility of mathematics in everyday life and specialized fields. This comprehensive guide will equip you with not just the solution but also the knowledge to tackle similar problems and appreciate the broader implications of division.
Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts or determining how many times one quantity is contained within another. The number being divided is called the dividend (in our case, 70000), the number by which we divide is the divisor (12), and the result is the quotient. Any remaining amount after the division is the remainder.
The expression 70000 / 12 asks: "How many times does 12 fit into 70000?" While a calculator readily provides the answer, understanding the process behind obtaining that answer is crucial for developing strong mathematical skills.
Calculating 70000 / 12: Step-by-Step
Let's break down the calculation of 70000 / 12 using long division, a method that illustrates the underlying process clearly:
-
Set up the long division: Write 70000 as the dividend inside the long division symbol (⟌) and 12 as the divisor to the left.
-
Divide the first digit(s): 12 does not go into 7, so we consider the first two digits: 70. How many times does 12 go into 70? It goes 5 times (5 x 12 = 60). Write 5 above the 0 in 70000.
-
Multiply and subtract: Multiply the quotient digit (5) by the divisor (12): 5 x 12 = 60. Subtract this from 70: 70 - 60 = 10.
-
Bring down the next digit: Bring down the next digit from the dividend (0) to create 100.
-
Repeat the process: How many times does 12 go into 100? It goes 8 times (8 x 12 = 96). Write 8 above the next 0. Subtract 96 from 100: 100 - 96 = 4.
-
Bring down the next digit: Bring down the next 0 to get 40.
-
Repeat the process: How many times does 12 go into 40? It goes 3 times (3 x 12 = 36). Write 3 above the next 0. Subtract 36 from 40: 40 - 36 = 4.
-
Bring down the last digit: Bring down the last 0 to create 40.
-
Repeat the process: How many times does 12 go into 40? It goes 3 times (3 x 12 = 36). Write 3 above the last 0. Subtract 36 from 40: 40 - 36 = 4.
-
The remainder: We have a remainder of 4.
Therefore, 70000 / 12 = 5833 with a remainder of 4. This can also be expressed as 5833 and 4/12, which simplifies to 5833 and 1/3. As a decimal, it's approximately 5833.333...
Beyond the Calculation: Understanding the Remainder
The remainder (4 in this case) is a crucial part of the division process. It indicates that after dividing 70000 into groups of 12, there are 4 units left over that cannot be evenly distributed. Understanding the remainder is essential in various applications, including:
-
Sharing items: If you have 70000 candies to distribute equally among 12 children, each child gets 5833 candies, and you have 4 candies left over.
-
Measurement: If you have a 70000-centimeter rope and need to cut it into 12-centimeter pieces, you can make 5833 pieces, with 4 centimeters remaining.
-
Programming: In computer programming, remainders are frequently used in algorithms and operations involving modular arithmetic.
Applications of Division in Real Life and Specialized Fields
Division is a fundamental operation used extensively in various aspects of life:
-
Finance: Calculating unit prices, dividing profits among partners, determining monthly payments on loans, and calculating interest rates all involve division.
-
Engineering: Dividing distances to determine the number of components needed, calculating material requirements, and determining the strength of structures often require precise division calculations.
-
Science: Determining concentrations in chemistry, analyzing data in physics and biology, and calculating rates of change rely heavily on division.
-
Everyday life: Sharing food, splitting bills, measuring ingredients in cooking, and calculating distances all use division implicitly or explicitly.
Exploring Related Mathematical Concepts
Understanding 70000 / 12 enhances our grasp of several related mathematical concepts:
-
Fractions: The remainder (4) can be expressed as a fraction (4/12), which simplifies to 1/3. This highlights the close relationship between division and fractions.
-
Decimals: The result can be expressed as a decimal (5833.333...), which represents the division process extended to include fractional parts.
-
Ratio and Proportion: Division is essential in understanding ratios and proportions. For example, the ratio of 70000 to 12 can be simplified or used to solve proportional problems.
-
Percentage: Calculating percentages often involves division. For instance, finding what percentage 12 is of 70000 involves dividing 12 by 70000 and multiplying by 100.
Frequently Asked Questions (FAQ)
Q: What is the exact answer to 70000 / 12?
A: The exact answer is 5833 with a remainder of 4, or 5833 1/3. As a decimal, it's a repeating decimal: 5833.333...
Q: Can I use a calculator to solve this?
A: Yes, a calculator provides a quick and efficient way to obtain the answer. However, understanding the manual calculation method is crucial for developing mathematical intuition and problem-solving skills.
Q: What if the dividend or divisor were different?
A: The same long division method can be applied to any division problem. The steps remain consistent, regardless of the numbers involved.
Q: Are there different methods of dividing numbers?
A: Yes, besides long division, other methods include short division (a more concise version of long division), synthetic division (used for polynomial division), and using algorithms in computer programming.
Q: Why is it important to understand long division?
A: Understanding long division fosters a deeper understanding of the concept of division and its relationship to other mathematical concepts. It improves problem-solving skills and builds a strong foundation for more advanced mathematics.
Conclusion: Mastering Division and its Applications
The seemingly straightforward calculation of 70000 / 12 opens a door to a much broader understanding of division, its applications, and its connection to other mathematical concepts. By understanding the process of long division, the significance of the remainder, and the various ways division is applied in everyday life and specialized fields, we gain a more profound appreciation for the power and versatility of this fundamental arithmetic operation. Mastering division not only helps in solving specific problems but also strengthens mathematical reasoning and problem-solving skills, equipping us to tackle more complex challenges in the future. The ability to perform and understand division is a fundamental skill that transcends the specific example of 70000 / 12, forming a crucial building block for mathematical proficiency.
Latest Posts
Latest Posts
-
35 Of 75
Sep 16, 2025
-
400 X 7
Sep 16, 2025
-
128km In Miles
Sep 16, 2025
-
750 5
Sep 16, 2025
-
Carrom Board Powder
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 70000 / 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.