35 Of 75
interactiveleap
Sep 16, 2025 · 5 min read
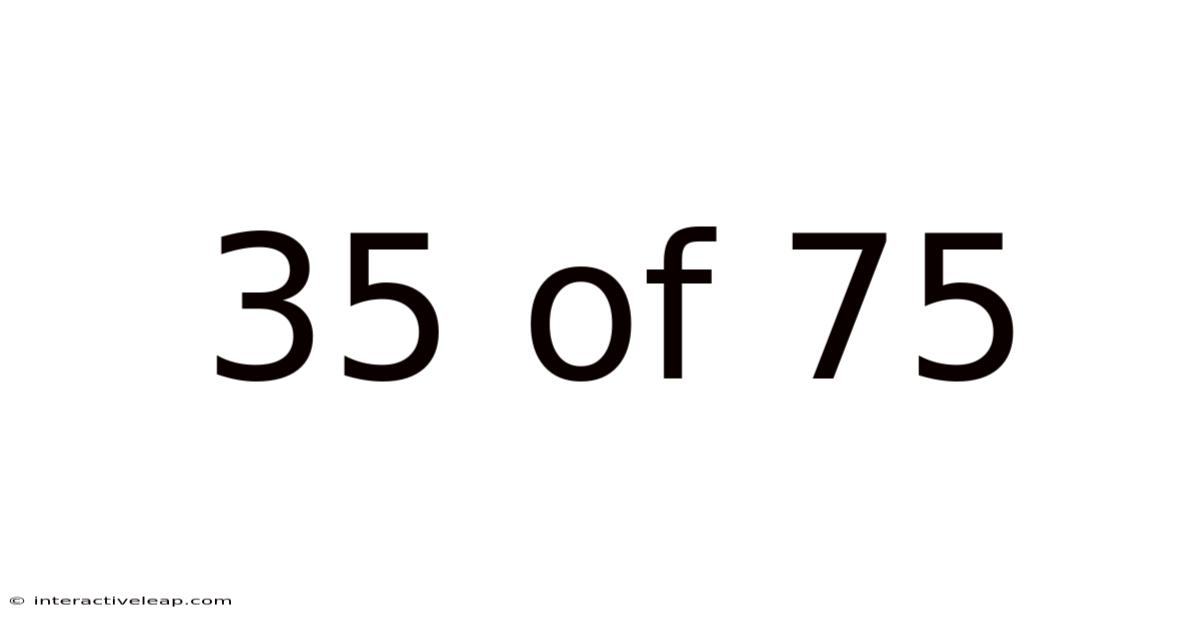
Table of Contents
Decoding the Fraction: 35 out of 75 – Understanding Percentages, Ratios, and Applications
Understanding fractions is a fundamental skill in mathematics, applicable in numerous everyday situations. This article delves into the specific fraction 35 out of 75, explaining its meaning, calculating its equivalent percentage and ratio, and exploring various real-world applications. We'll also touch upon related concepts to broaden your understanding of this seemingly simple yet versatile numerical concept. Understanding fractions like 35/75 allows for a deeper comprehension of proportions, percentages, and data interpretation.
Understanding the Fraction 35/75
The fraction 35 out of 75, written mathematically as 35/75, represents a part of a whole. The numerator (35) indicates the number of parts we're considering, while the denominator (75) represents the total number of parts making up the whole. In simple terms, if you have 75 items and you select 35 of them, you've chosen 35/75 of the total.
Simplifying the Fraction
Before we proceed, it's important to simplify the fraction to its lowest terms. This makes calculations easier and provides a clearer representation of the proportion. Both 35 and 75 are divisible by 5:
35 ÷ 5 = 7 75 ÷ 5 = 15
Therefore, 35/75 simplifies to 7/15. This simplified fraction represents the same proportion as 35/75, but in a more concise form.
Calculating the Percentage
To express 35/75 (or 7/15) as a percentage, we need to convert the fraction into a decimal and then multiply by 100.
-
Method 1 (Using the simplified fraction):
7 ÷ 15 ≈ 0.4667 0.4667 x 100 ≈ 46.67%
-
Method 2 (Using the original fraction):
35 ÷ 75 ≈ 0.4667 0.4667 x 100 ≈ 46.67%
Therefore, 35 out of 75 represents approximately 46.67%. This means that 35 is approximately 46.67% of 75.
Understanding the Ratio
The ratio of 35 to 75 can be expressed as 35:75. Similar to the fraction, this ratio indicates the relationship between two quantities. Just like the fraction, we can simplify this ratio by dividing both numbers by their greatest common divisor (5):
35 ÷ 5 = 7 75 ÷ 5 = 15
Thus, the simplified ratio is 7:15. This means for every 7 parts of one quantity, there are 15 parts of another quantity.
Real-World Applications
The fraction 35/75, and its simplified form 7/15, has numerous applications in everyday life and various fields:
-
Test Scores: Imagine a test with 75 questions. If a student answers 35 questions correctly, their score would be 35/75 or 46.67%.
-
Sales and Marketing: If a company sets a sales target of 75 units and sells 35 units, their sales performance is 35/75 or 46.67% of the target.
-
Surveys and Statistics: In a survey of 75 people, 35 responded positively to a particular question. This represents 35/75 or 46.67% positive responses.
-
Manufacturing and Quality Control: If a factory produces 75 items and 35 are found to be defective, the defect rate is 35/75 or 46.67%.
-
Financial Analysis: Analyzing investment portfolios, budgeting, or tracking expenses often involves working with fractions and percentages representing portions of a total amount.
Further Exploration of Related Concepts
Understanding 35/75 opens doors to explore more advanced mathematical concepts:
-
Proportions: A proportion is a statement that two ratios are equal. For instance, 35/75 = 7/15 is a proportion. Understanding proportions is crucial in scaling recipes, converting units, and solving various problems involving ratios.
-
Percentage Change: This concept measures the relative change between an old and a new value. For example, if the number of units sold increases from 35 to 50, the percentage change would be calculated using the formula: [(New Value - Old Value) / Old Value] x 100.
-
Probability: Fractions are fundamental in probability. If there are 75 possible outcomes and 35 favorable outcomes, the probability of a favorable outcome is 35/75 or 7/15.
-
Data Analysis and Interpretation: Charts, graphs, and other data visualizations often represent data using fractions or percentages. Understanding fractions is essential for interpreting this data accurately.
-
Algebraic Equations: Fractions often appear in algebraic equations. Solving these equations requires a firm understanding of fraction manipulation and simplification.
Frequently Asked Questions (FAQ)
-
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator and then multiply the result by 100.
-
Q: How do I simplify a fraction?
A: Find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
-
Q: What is the difference between a fraction and a ratio?
A: A fraction represents a part of a whole, while a ratio compares two quantities. Although they are closely related and often expressed similarly, ratios can compare quantities that are not necessarily parts of the same whole.
-
Q: Can I use a calculator to simplify fractions?
A: Many calculators have a fraction function that can simplify fractions automatically. Alternatively, you can use online fraction calculators.
Conclusion
The seemingly simple fraction 35/75, simplified to 7/15, offers a rich understanding of various mathematical concepts including percentages, ratios, proportions, and their applications across numerous fields. Mastering these concepts provides a solid foundation for more complex mathematical problems and enhances the ability to interpret and analyze data effectively in various real-world scenarios. By understanding the relationship between fractions, percentages, and ratios, you'll be better equipped to handle tasks involving proportions, data analysis, and problem-solving in everyday life and professional settings. The journey from understanding a simple fraction like 35/75 to grasping its deeper implications is a testament to the power and versatility of mathematical literacy.
Latest Posts
Latest Posts
-
75 Of 8
Sep 16, 2025
-
14 2kg In Stone
Sep 16, 2025
-
15 Off 55
Sep 16, 2025
-
Baby Weight Conversion
Sep 16, 2025
-
Urban Legend Dti
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.