70 Of 420
interactiveleap
Sep 17, 2025 · 5 min read
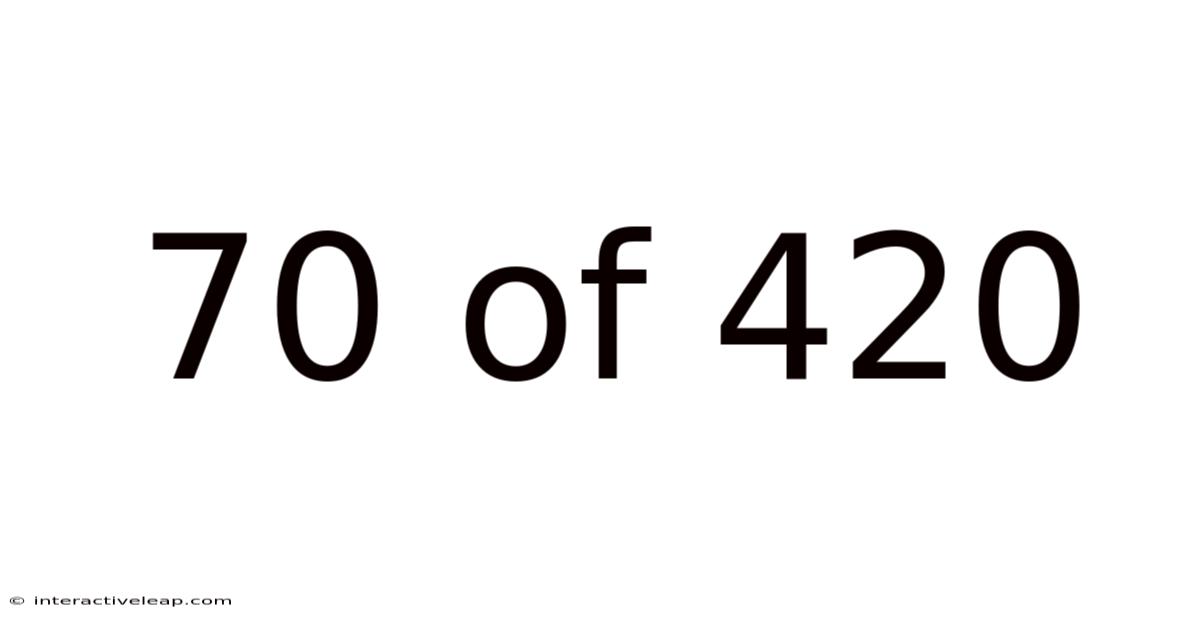
Table of Contents
Decoding 70/420: Understanding Fraction Simplification and its Applications
Understanding fractions is a fundamental concept in mathematics, crucial for various applications in daily life and advanced studies. This article delves into the simplification of the fraction 70/420, explaining the process step-by-step and highlighting its broader implications within the realm of mathematical concepts. We'll explore the method of finding the greatest common divisor (GCD), its significance in simplifying fractions, and how this seemingly simple operation forms the basis of more complex mathematical procedures. This detailed explanation will be beneficial for students, educators, and anyone seeking a deeper understanding of fraction simplification.
Introduction: What is 70/420?
The fraction 70/420 represents a part of a whole. The numerator (70) indicates the number of parts we have, while the denominator (420) represents the total number of equal parts in the whole. This fraction, in its current form, is not in its simplest form. Simplifying a fraction means reducing it to its equivalent form where the numerator and denominator have no common factors other than 1. This process makes the fraction easier to understand and work with in calculations.
Step-by-Step Simplification of 70/420
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Let's find the GCD of 70 and 420 using the prime factorization method:
1. Prime Factorization:
- 70: The prime factorization of 70 is 2 x 5 x 7.
- 420: The prime factorization of 420 is 2 x 2 x 3 x 5 x 7.
2. Identifying Common Factors:
By comparing the prime factorizations, we can identify the common factors: 2, 5, and 7.
3. Calculating the GCD:
The GCD is the product of the common prime factors: 2 x 5 x 7 = 70.
4. Simplifying the Fraction:
Now, we divide both the numerator and the denominator by the GCD (70):
70 ÷ 70 = 1 420 ÷ 70 = 6
Therefore, the simplified form of the fraction 70/420 is 1/6.
Alternative Methods for Finding the GCD
While prime factorization is a reliable method, other techniques can be used to find the GCD, particularly for larger numbers. These include:
-
Euclidean Algorithm: This iterative method involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
-
Listing Factors: List all the factors of both the numerator and denominator. The largest number appearing in both lists is the GCD. This method is practical for smaller numbers but becomes less efficient for larger ones.
The Significance of Fraction Simplification
Simplifying fractions is not merely a mathematical exercise; it holds significant importance in various contexts:
-
Clarity and Understanding: A simplified fraction is easier to understand and visualize. 1/6 is much clearer than 70/420. This improved clarity is especially valuable in conveying information and interpreting results.
-
Ease of Calculation: Simplified fractions make calculations significantly easier. Adding, subtracting, multiplying, and dividing simplified fractions are much more straightforward than working with complex, unsimplified fractions.
-
Consistency in Results: Presenting results in their simplest form ensures consistency and avoids ambiguity. This is particularly crucial in fields like engineering, physics, and finance where accuracy is paramount.
-
Foundation for Advanced Concepts: Fraction simplification forms the bedrock of more advanced mathematical concepts, including algebra, calculus, and even abstract algebra. A solid grasp of this fundamental concept is essential for progress in these areas.
Applications of Fraction Simplification in Real-World Scenarios
Fraction simplification is not confined to the classroom; it has widespread applications in various real-world scenarios:
-
Cooking and Baking: Recipes often involve fractions. Simplifying fractions helps in accurately measuring ingredients and scaling recipes.
-
Construction and Engineering: Accurate measurements and calculations are critical in construction and engineering projects. Simplifying fractions ensures precision in design and execution.
-
Finance and Accounting: Financial calculations often involve fractions, especially when dealing with percentages, interest rates, and proportions. Simplifying fractions ensures accuracy in financial analysis and reporting.
-
Data Analysis: Data analysis frequently utilizes fractions and ratios. Simplifying fractions facilitates easier interpretation and visualization of data.
Frequently Asked Questions (FAQ)
Q1: What happens if I simplify a fraction incorrectly?
A1: Incorrect simplification leads to inaccurate results in further calculations. Always double-check your work to ensure the fraction is simplified correctly.
Q2: Can I simplify a fraction by dividing the numerator and denominator by any common factor?
A2: Yes, but the most efficient approach is to divide by the greatest common divisor (GCD) to obtain the simplest form in a single step.
Q3: Are there any situations where leaving a fraction unsimplified is acceptable?
A3: In some contexts, especially when comparing fractions or demonstrating a specific step in a calculation, leaving the fraction unsimplified might be acceptable for clarity, but generally, simplifying fractions is the preferred practice.
Q4: What if the GCD is 1?
A4: If the GCD of the numerator and denominator is 1, it means the fraction is already in its simplest form. This indicates that there are no common factors other than 1, and no further simplification is possible.
Conclusion: Mastering Fraction Simplification
Mastering fraction simplification is a crucial skill in mathematics, impacting various aspects of our lives and studies. The simplification of 70/420 to 1/6 illustrates the fundamental principle of reducing a fraction to its simplest form by finding and dividing by the greatest common divisor. This process is not just about reducing numbers; it underpins a deeper understanding of mathematical concepts and improves the clarity, accuracy, and efficiency of calculations across numerous disciplines. By understanding the methods involved and their significance, students and anyone working with fractions can greatly enhance their problem-solving abilities and appreciation of mathematical principles. The ability to confidently simplify fractions forms a solid foundation for tackling more complex mathematical challenges in the future. Continuous practice and exploration of different methods for finding the GCD will further solidify this crucial mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about 70 Of 420 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.