35 Of 250
interactiveleap
Sep 17, 2025 · 5 min read
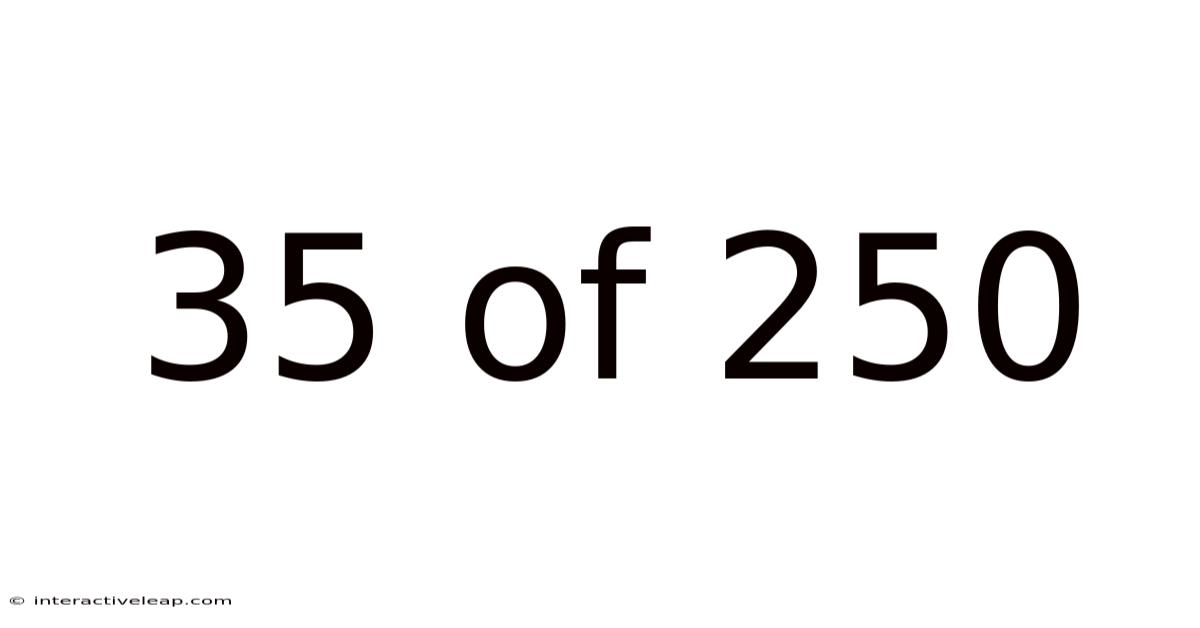
Table of Contents
Decoding 35 out of 250: Understanding Proportions, Percentages, and Their Real-World Applications
Understanding proportions and percentages is fundamental to navigating the complexities of everyday life, from calculating sale discounts to analyzing statistical data. This article delves deep into the meaning of a score like "35 out of 250," exploring how to convert it into a percentage, understanding its implications, and showcasing its relevance across various fields. We'll move beyond simple calculations and explore the conceptual understanding needed for truly grasping the significance of such figures.
Introduction: What Does 35 out of 250 Mean?
"35 out of 250" represents a ratio, indicating that 35 instances occurred out of a total possible 250 instances. This type of ratio is commonly encountered in various contexts, such as exam scores, survey results, and performance metrics. Understanding how to interpret and represent this ratio is crucial for making informed decisions and drawing meaningful conclusions. This article will guide you through the process, equipping you with the skills to effectively analyze similar proportions and apply this knowledge to real-world situations.
Converting to Percentage: The Simple Calculation
The most common way to represent "35 out of 250" is as a percentage. This involves calculating the proportion and then multiplying by 100. The calculation is straightforward:
(35/250) * 100 = 14%
Therefore, 35 out of 250 is equivalent to 14%. This percentage provides a readily understandable representation of the ratio, facilitating comparisons and interpretations. Understanding this conversion is the first step towards a comprehensive understanding of proportional data.
Beyond the Calculation: Understanding the Context
While the calculation itself is simple, the true significance of "35 out of 250" (or 14%) depends entirely on the context. A 14% score on a difficult exam might be commendable, while a 14% success rate in a business venture might be cause for concern. The context determines the interpretation:
- Academic Performance: A student scoring 35 out of 250 on a test might need to improve their understanding of the subject matter. The specific grading scale of the institution would determine the letter grade, but the percentage allows for objective comparison with other students.
- Business Metrics: In a sales context, 35 successful sales out of 250 attempts reveals a conversion rate of 14%. This could inform sales strategies, potentially highlighting areas for improvement in lead generation or sales techniques.
- Survey Results: If 35 out of 250 respondents answered "yes" to a particular survey question, this indicates a 14% positive response rate. This percentage provides valuable information about public opinion or customer preferences.
- Quality Control: In manufacturing, 35 defective items out of 250 produced signifies a 14% defect rate. This metric is crucial for identifying areas needing improvement in the production process to reduce waste and enhance quality.
Working with Proportions: Applications and Examples
Proportions are not limited to simple conversions to percentages. They form the foundation for numerous practical applications, including:
- Scaling Recipes: If a recipe calls for 35 grams of flour for 250 grams of dough, you can use proportions to scale the recipe up or down.
- Map Scales: Maps use proportions to represent distances on a smaller scale. A map scale might indicate that 1 centimeter represents 250 kilometers, allowing for accurate distance calculations.
- Financial Calculations: Calculating interest, discounts, or profit margins all involve proportional reasoning. A 14% discount on a $250 item would be $35.
- Scientific Experiments: Proportions are essential in scientific experiments, for example, in determining the concentration of a solution.
Advanced Applications: Statistical Analysis and Probability
The concept of proportions extends beyond simple calculations and finds application in advanced statistical analyses and probability calculations. Understanding the distribution of data, standard deviations, and confidence intervals all rely on a fundamental understanding of proportions. For instance:
- Confidence Intervals: Researchers frequently use proportions to estimate the confidence intervals of their findings. A 14% response rate in a survey might have a confidence interval that suggests the true population response rate lies between 10% and 18%.
- Hypothesis Testing: Proportions play a vital role in hypothesis testing, allowing researchers to assess the likelihood of observing a certain result given a particular hypothesis.
- Predictive Modeling: In various fields, including finance and marketing, predictive models frequently leverage proportions to forecast future outcomes.
Frequently Asked Questions (FAQ)
Q: How can I calculate the percentage increase or decrease from a previous proportion?
A: To calculate the percentage change, first determine the difference between the new and old values. Then, divide this difference by the old value and multiply by 100. For example, if the proportion increased from 35 out of 250 to 40 out of 250, the percentage increase would be: [(40-35)/35] * 100 ≈ 14.3%.
Q: What if the denominator is zero?
A: If the denominator (the total number of possible instances) is zero, the proportion is undefined. This signifies the absence of data or an impossible scenario.
Q: Are there online tools to help with these calculations?
A: Yes, many free online calculators can assist with calculating percentages and proportions. These tools can be useful for quick calculations and verifying your own work.
Q: How do I represent this data visually?
A: Visual representations, such as pie charts or bar graphs, are excellent ways to communicate the proportion of 35 out of 250 (14%). These charts make complex data more accessible and easier to understand.
Conclusion: Mastering Proportions for Real-World Success
Understanding "35 out of 250" involves more than just a simple calculation. It's about grasping the underlying concepts of ratios, proportions, and percentages, and recognizing their wide-ranging applications across diverse fields. From everyday tasks to complex statistical analyses, the ability to interpret and utilize proportional data is a valuable skill that empowers informed decision-making and enhances problem-solving capabilities. This article has provided a comprehensive foundation for understanding these concepts, but continued practice and application are key to mastering this essential skill. By consistently engaging with proportional data in various contexts, you'll build your confidence and further enhance your ability to analyze information critically and effectively. Remember, the power of understanding proportions lies not just in the calculation itself, but in its ability to illuminate meaningful insights from the data at hand.
Latest Posts
Latest Posts
-
183cm To In
Sep 17, 2025
-
Test In Spanish
Sep 17, 2025
-
1 55kg To Lbs
Sep 17, 2025
-
Microns To Millimeters
Sep 17, 2025
-
180grams To Oz
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.