3 X 4/15
interactiveleap
Sep 17, 2025 · 5 min read
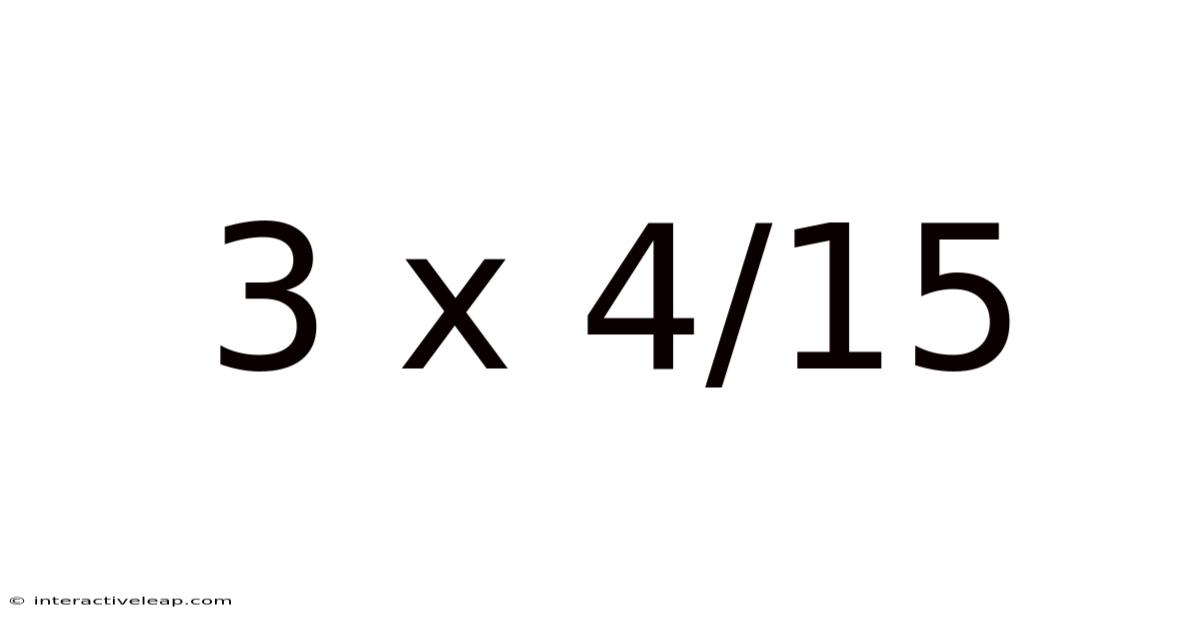
Table of Contents
Unveiling the Mystery: A Deep Dive into 3 x 4/15
This article explores the seemingly simple mathematical expression "3 x 4/15," delving beyond a simple numerical answer to uncover the underlying principles and practical applications. We'll unpack the order of operations, discuss different approaches to solving the problem, and explore the broader context of fractions and multiplication within the realm of mathematics. Understanding this seemingly basic calculation provides a strong foundation for more complex mathematical concepts.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before we jump into solving 3 x 4/15, it's crucial to understand the order of operations. This set of rules dictates the sequence in which we perform calculations to ensure a consistent and accurate result. The acronyms PEMDAS and BODMAS are commonly used to remember the order:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)
- BODMAS: Brackets, Orders, Division and Multiplication (from left to right), Addition and Subtraction (from left to right)
Both acronyms represent the same order of operations; the only difference is the terminology used. In our example, "3 x 4/15," we have multiplication and division. According to PEMDAS/BODMAS, we perform these operations from left to right.
Solving 3 x 4/15: Step-by-Step Approach
Following the order of operations, we begin with the multiplication:
- Multiplication: 3 x 4 = 12
This simplifies our expression to: 12/15
- Division: 12/15
Now, we perform the division. We can simplify this fraction by finding the greatest common divisor (GCD) of 12 and 15. The GCD of 12 and 15 is 3. Dividing both the numerator and the denominator by 3 gives us:
12 ÷ 3 = 4 15 ÷ 3 = 5
Therefore, the simplified fraction is 4/5.
Thus, the solution to 3 x 4/15 is 4/5.
Alternative Approaches to Solving the Problem
While the above method is straightforward and adheres strictly to the order of operations, there are other ways to approach this problem:
-
Simplifying Before Multiplying: We can simplify the fraction 4/15 before performing the multiplication. Since 4 and 15 share no common factors other than 1, we can't simplify this specific fraction further before multiplication. However, this approach is valuable in more complex problems where simplification beforehand can significantly reduce the complexity of the calculation.
-
Converting to Decimals: We can convert the fraction 4/15 to a decimal and then multiply. 4/15 ≈ 0.2667. Then, 3 x 0.2667 ≈ 0.8. While this approach provides a numerical answer, it's important to note that the decimal representation is an approximation, and the fractional form (4/5) is more precise.
The Importance of Understanding Fractions
This simple problem highlights the importance of a strong understanding of fractions. Fractions represent parts of a whole and are fundamental to many areas of mathematics and beyond. Understanding how to simplify, multiply, and divide fractions is crucial for success in algebra, calculus, and various applications in science and engineering.
Practical Applications of Fractions and Multiplication
Fractions and multiplication are not confined to the realm of abstract mathematics; they have widespread practical applications:
-
Baking and Cooking: Recipes often involve fractions – 1/2 cup of sugar, 2/3 cup of flour, etc. Accurate measurements are crucial for successful baking, requiring a solid understanding of fractions and multiplication to adjust recipes.
-
Construction and Engineering: Precision is paramount in construction and engineering. Calculations frequently involve fractions and multiplication to determine accurate dimensions, material quantities, and structural integrity.
-
Finance and Budgeting: Managing finances often requires calculating percentages and proportions, which rely heavily on fractions and multiplication.
-
Data Analysis: In statistics and data analysis, fractions and proportions are used to represent data, analyze trends, and make informed decisions.
Frequently Asked Questions (FAQ)
Q: Why is the order of operations important?
A: The order of operations ensures consistency in mathematical calculations. Without a defined order, different individuals could arrive at different answers for the same problem, leading to confusion and errors.
Q: What if the problem was 3 + 4/15?
A: In this case, we would perform the division before the addition, following PEMDAS/BODMAS. 4/15 would remain as a fraction, and the result would be 3 + 4/15, which can also be written as an improper fraction: 49/15.
Q: Can I use a calculator to solve this problem?
A: Yes, a calculator can solve this problem. However, understanding the underlying principles and performing the calculations manually is essential for developing a strong mathematical foundation. Calculators are tools, but they shouldn't replace understanding.
Q: What are some common mistakes students make when dealing with fractions?
A: Some common mistakes include:
- Forgetting to simplify fractions.
- Incorrectly applying the order of operations.
- Making errors when multiplying or dividing fractions.
- Misunderstanding the concept of equivalent fractions.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through numerous problems of varying complexity, focusing on each step of the process. Use visual aids like diagrams and manipulatives to solidify your understanding of the concepts.
Expanding on the Concepts: Beyond 3 x 4/15
The seemingly simple expression "3 x 4/15" opens doors to a deeper exploration of mathematical concepts:
-
Number Systems: This problem involves integers and rational numbers (fractions). Understanding the properties of different number systems is crucial for advanced mathematical work.
-
Algebra: Generalizing this problem to include variables leads to algebraic expressions and equations. For instance, consider "a x b/c," where a, b, and c represent variables.
-
Calculus: The concepts of limits and derivatives in calculus are built upon a strong foundation in algebra and arithmetic, including fractions and operations with them.
Conclusion: More Than Just Numbers
Solving "3 x 4/15" is more than just arriving at the answer 4/5. The process reveals fundamental mathematical principles, emphasizes the importance of order of operations, and underscores the ubiquitous nature of fractions in everyday life and advanced mathematical studies. By understanding the steps involved and the broader context, we build a solid foundation for tackling more complex mathematical problems and applications across various fields. Mastering these seemingly simple calculations is the cornerstone of mathematical fluency and problem-solving skills. It’s not just about the answer; it’s about the journey of understanding the process, the logic, and the power of mathematical principles.
Latest Posts
Latest Posts
-
28 Times 5
Sep 17, 2025
-
24 Of 75
Sep 17, 2025
-
3 Dl Ml
Sep 17, 2025
-
Hard To Beat
Sep 17, 2025
-
10 Off 140
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 X 4/15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.