64 X 4
interactiveleap
Sep 20, 2025 · 7 min read
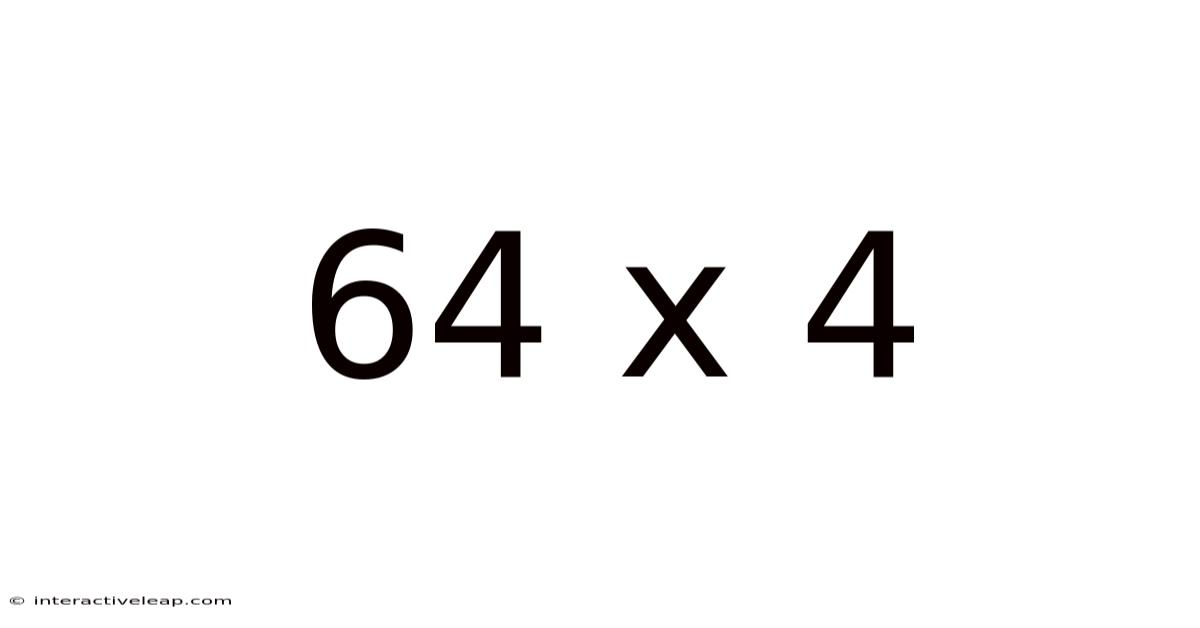
Table of Contents
Decoding 64 x 4: Unveiling the Power of Multiplication and its Real-World Applications
This article delves into the seemingly simple multiplication problem of 64 x 4, exploring its various facets beyond a straightforward numerical answer. We'll examine the different methods for solving it, its implications in various fields, and how understanding this seemingly basic calculation can unlock a deeper appreciation for mathematics and its practical applications in everyday life. This exploration will touch upon fundamental arithmetic, advanced mathematical concepts, and real-world scenarios where this specific calculation – and the principles behind it – become surprisingly relevant.
I. Understanding the Fundamentals: 64 x 4
At its core, 64 x 4 represents a repeated addition. It asks: what is the sum of four 64s? This can be visually represented as four groups of 64 objects, whether they be apples, marbles, or abstract units. The fundamental operation is multiplication, a cornerstone of arithmetic used extensively in various fields.
Methods for Solving 64 x 4:
Several methods can be employed to solve this multiplication problem:
-
Traditional Multiplication: This involves the standard algorithm taught in schools. We multiply 4 by each digit of 64, starting from the right: 4 x 4 = 16 (write down 6, carry-over 1); 4 x 6 = 24, plus the carried-over 1 equals 25. The answer is 256.
-
Distributive Property: We can break down 64 into 60 + 4, then apply the distributive property: 4 x (60 + 4) = (4 x 60) + (4 x 4) = 240 + 16 = 256. This method highlights the underlying properties of multiplication.
-
Repeated Addition: This is the most basic approach: 64 + 64 + 64 + 64 = 256. It clearly demonstrates the relationship between multiplication and addition.
-
Mental Math Techniques: With practice, one can develop mental math strategies to solve this quickly. For instance, doubling 64 twice: 64 x 2 = 128; 128 x 2 = 256. This technique showcases the power of efficient calculation strategies.
II. Beyond the Numbers: Exploring the Significance
While seemingly simple, the calculation 64 x 4 has far-reaching implications when we consider its broader mathematical context and its applications in diverse fields:
-
Binary Systems and Computer Science: The number 64 (2<sup>6</sup>) holds particular significance in computer science due to its relationship with binary numbers. It represents a power of 2, a fundamental unit in binary systems. Understanding this calculation helps to grasp memory allocation, data structures, and other crucial aspects of computing. For instance, 64 bits are commonly used to represent data units, and 4 might represent a specific operation or data type. Understanding 64 x 4 in this context could translate to calculating the total memory space required for a particular data operation.
-
Geometry and Measurement: Imagine a rectangular area with dimensions 64 units by 4 units. The calculation 64 x 4 would give us the total area of this rectangle. This directly translates to practical applications in construction, landscaping, and other fields requiring area calculations. Consider a room measuring 64 inches by 4 inches; calculating 64 x 4 provides the area in square inches.
-
Financial Calculations: This seemingly simple calculation can underpin more complex financial computations. For instance, if a company earns $64 per unit and sells 4 units, the calculation yields the total revenue. Scaling this up to hundreds or thousands of units demonstrates the practical application of basic multiplication in business.
-
Data Analysis and Statistics: In statistics, multiplication is frequently used in calculating averages, probabilities, and other crucial metrics. Understanding this calculation forms the basis for more advanced statistical analysis where larger datasets are involved. Suppose a study involves 4 groups of 64 participants each. This calculation is crucial for determining the total number of participants.
-
Everyday Applications: Beyond academic settings, 64 x 4 shows up in numerous everyday scenarios. Calculating the total cost of four items priced at $64 each, determining the total number of days in four months of 64 days each (a hypothetical scenario, but illustrates the concept), or even figuring out the total number of squares in a grid with dimensions 64 x 4, are all instances of this basic calculation in action.
III. Expanding the Understanding: Related Concepts
The calculation 64 x 4 serves as a stepping stone towards understanding more complex mathematical concepts:
-
Powers and Exponents: The number 64 is 2<sup>6</sup>, representing 2 multiplied by itself six times. This introduces the concept of exponents and their significance in expressing large numbers concisely. Understanding this relationship provides a deeper appreciation for exponential growth and decay.
-
Factors and Multiples: The numbers 64 and 4 have a relationship as factors and multiples. 4 is a factor of 64 (64 is divisible by 4), while 64 is a multiple of 4. Exploring factorizations and prime factorizations contributes to a more robust understanding of number theory.
-
Algebra and Equations: The problem can be expressed algebraically as x = 64 x 4, where 'x' represents the unknown value. Solving algebraic equations builds upon the fundamental understanding of arithmetic operations.
-
Order of Operations (PEMDAS/BODMAS): While this specific problem doesn't directly involve order of operations, understanding the hierarchy of mathematical operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is crucial for solving more complex equations involving multiple operations.
IV. Practical Problem-Solving: Real-World Examples
Let's consider some real-world scenarios where this multiplication problem and the underlying principles are applied:
-
Construction: A contractor needs to estimate the number of bricks required for a wall measuring 64 feet in length and 4 feet in height. Assuming each brick covers one square foot, the calculation 64 x 4 yields the required number of bricks (256).
-
Packaging: A factory produces boxes with dimensions 64 cm x 4 cm. Calculating the area of the box's base (64 x 4 = 256 sq cm) is crucial for optimizing material usage and packaging design.
-
Inventory Management: A warehouse contains 4 pallets, each holding 64 units of a particular product. The calculation 64 x 4 helps determine the total number of units in stock (256).
-
Event Planning: If an event requires 4 rows of seats, each containing 64 seats, then 64 x 4 determines the total seating capacity (256).
-
Recipe Scaling: A recipe calls for 4 cups of flour, and you need to increase the recipe to serve 64 times the original amount. Then, you calculate 4 x 64 to get the total amount of flour needed (256 cups).
V. Frequently Asked Questions (FAQ)
-
What is the quickest way to solve 64 x 4? Doubling 64 twice (64 x 2 = 128, 128 x 2 = 256) is a fast mental math approach.
-
What are some real-world applications beyond simple calculations? The principles behind this calculation are used in complex engineering, financial modeling, and scientific research.
-
How does understanding this calculation help in advanced mathematics? It builds a strong foundation in arithmetic, which is essential for mastering algebra, calculus, and other advanced mathematical fields.
-
Is there a different way to represent this calculation? Yes, it can be expressed algebraically (x = 64 x 4) or visually using arrays or diagrams.
-
Why is it important to learn different methods for solving multiplication problems? Learning multiple methods enhances understanding and problem-solving skills, allowing for flexibility and efficiency in various situations.
VI. Conclusion: The Enduring Power of a Simple Calculation
The seemingly simple problem of 64 x 4 holds a surprising depth and breadth of applications. From its fundamental role in arithmetic to its significance in advanced fields like computer science and engineering, understanding this calculation provides a foundational understanding of mathematics and its practical implications. By exploring various solution methods and its real-world applications, we unveil the enduring power of a seemingly simple mathematical operation, highlighting the interconnectedness of mathematical concepts and their pervasive influence in our lives. Mastering this calculation isn't just about arriving at the answer 256; it’s about developing a deeper appreciation for the principles of multiplication, its applications, and its role in shaping our understanding of the world around us. The ability to quickly and accurately solve this problem serves as a building block for tackling more complex challenges and fostering a strong numerical aptitude.
Latest Posts
Latest Posts
-
10000km In Miles
Sep 20, 2025
-
25 Of 3600
Sep 20, 2025
-
X 3 X
Sep 20, 2025
-
18 5cm To Inches
Sep 20, 2025
-
X2 X 25
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 64 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.