X/3 - X
interactiveleap
Sep 20, 2025 · 6 min read
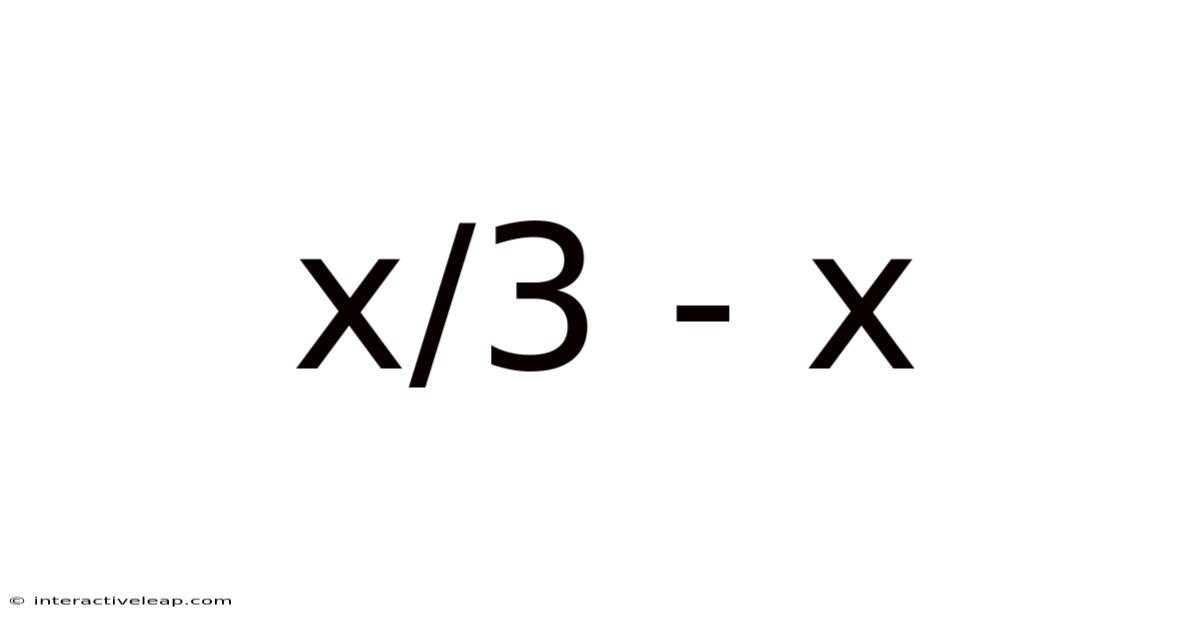
Table of Contents
Unveiling the Mystery: A Deep Dive into x/3 - x
Understanding algebraic expressions is fundamental to success in mathematics. This article will explore the seemingly simple expression x/3 - x, demystifying its various interpretations, manipulations, and applications. We'll delve into its simplification, explore its graphical representation, analyze its behavior for different values of x, and address common misconceptions. Whether you're a high school student tackling algebra or a curious individual looking to refresh your mathematical knowledge, this comprehensive guide will provide a solid understanding of this expression.
Introduction: What Does x/3 - x Really Mean?
At first glance, x/3 - x might seem straightforward. It represents the subtraction of x from one-third of x. However, a deeper understanding involves recognizing its versatility and the different contexts in which it can be applied. This expression can be used to model real-world scenarios, solve algebraic equations, and even explore fundamental concepts in calculus. We'll break down the expression step-by-step, clarifying its meaning and showing how to manipulate it effectively. This seemingly simple expression holds the key to understanding more complex algebraic manipulations.
Simplifying the Expression: Combining Like Terms
The power of algebra lies in its ability to simplify complex expressions into more manageable forms. The expression x/3 - x contains like terms; both terms involve the variable x. To simplify, we need to find a common denominator. Since x can be written as (3x)/3, we can rewrite the expression as:
x/3 - (3x)/3
Now that we have a common denominator, we can combine the numerators:
(x - 3x) / 3
This simplifies to:
-2x/3
Therefore, the simplified form of x/3 - x is -2x/3. This simplified form is crucial for solving equations and understanding the expression's behavior. Remember, this simplification is valid for all real values of x.
Graphical Representation: Visualizing the Expression
Visualizing mathematical expressions can significantly enhance understanding. Let's consider the graphical representation of y = -2x/3. This is a linear equation, representing a straight line. The slope of this line is -2/3, indicating a negative slope (the line goes downwards from left to right). The y-intercept is 0, meaning the line passes through the origin (0,0).
-
Slope: The slope of -2/3 tells us that for every 3 units increase in x, y decreases by 2 units. This reflects the proportional relationship between x and y in the expression.
-
Intercept: The y-intercept of 0 means that when x is 0, y is also 0. This makes intuitive sense; if x is zero, then -2x/3 is also zero.
Understanding the graph allows us to quickly determine the value of y for any given value of x, and vice versa. This visual representation complements the algebraic simplification, providing a different perspective on the expression's behavior.
Analyzing the Behavior for Different Values of x: Exploring the Function
Let's analyze how the value of the expression -2x/3 changes depending on the value of x:
-
When x = 0: The expression evaluates to -2(0)/3 = 0. This confirms our observation from the graphical representation that the line passes through the origin.
-
When x > 0: The expression will be negative. As x increases, the magnitude of the negative value also increases. For example, if x = 3, then -2x/3 = -2. If x = 6, then -2x/3 = -4.
-
When x < 0: The expression will be positive. As x becomes more negative, the value of the expression becomes more positive. For example, if x = -3, then -2x/3 = 2. If x = -6, then -2x/3 = 4.
This analysis highlights the inverse relationship between x and the expression's value. As x increases in the positive direction, the expression decreases (becomes more negative). As x increases in the negative direction, the expression increases (becomes more positive). This relationship is clearly visible in the graphical representation of the line.
Solving Equations Involving x/3 - x: Applications in Algebra
The expression x/3 - x can be part of more complex algebraic equations. Let's consider an example:
x/3 - x = 2
To solve this equation, we first simplify the left side using our previously derived simplified form:
-2x/3 = 2
Now, we can solve for x:
-2x = 6
x = -3
Therefore, the solution to the equation x/3 - x = 2 is x = -3. This demonstrates how simplifying the expression is crucial for efficient equation solving. More complex equations might involve this expression as one component, requiring a similar process of simplification and algebraic manipulation to find the solution.
Advanced Applications: Calculus and Beyond
While this article focuses on the basic understanding and manipulation of x/3 - x, it's important to note that this simple expression can be a building block for more advanced mathematical concepts. In calculus, for instance, understanding this linear function's derivative and integral would be crucial for further analysis. The derivative, representing the instantaneous rate of change, would be a constant (-2/3), highlighting the constant slope of the line. The integral would represent the area under the curve, providing another geometrical interpretation of the expression.
Common Misconceptions and Pitfalls
Several common mistakes occur when working with this expression:
-
Incorrect simplification: A frequent error is failing to find a common denominator before combining terms. This leads to incorrect simplification and inaccurate results. Always ensure you have a common denominator before combining fractions.
-
Sign errors: Subtracting x from x/3 often leads to sign errors. Remember that subtracting a positive x is the same as adding a negative x. Careful attention to signs is paramount in algebraic manipulation.
-
Misinterpretation of the graph: Incorrectly interpreting the slope and y-intercept of the graph can lead to misconceptions about the expression's behavior. Make sure to understand the meaning of the slope and intercept in the context of the expression.
Frequently Asked Questions (FAQ)
Q: Can x be any number in the expression x/3 - x?
A: Yes, x can represent any real number. The expression is defined for all real numbers.
Q: Is there another way to simplify x/3 - x?
A: While -2x/3 is the most simplified form, you could also factor out x: x(1/3 - 1) = x(-2/3) = -2x/3. Both forms are equivalent.
Q: What are some real-world applications of this expression?
A: While not directly representing a specific real-world phenomenon, expressions like this serve as building blocks for more complex models in various fields such as physics, engineering, and economics where proportional relationships exist. Imagine calculating the remaining portion of a resource after consuming one-third of the total.
Conclusion: Mastering the Fundamentals
The expression x/3 - x, though seemingly simple, offers a rich opportunity to understand fundamental algebraic concepts. Through simplification, graphical representation, and behavioral analysis, we've gained a comprehensive understanding of this expression. Mastering this fundamental concept forms a strong foundation for tackling more complex algebraic problems and delving into higher-level mathematical concepts. Remember the importance of meticulous simplification, attention to detail, and the power of visualization in mastering algebraic expressions. The journey towards mathematical proficiency begins with mastering the fundamentals.
Latest Posts
Latest Posts
-
4 2x 1
Sep 20, 2025
-
84 1kg In Stone
Sep 20, 2025
-
15 Of 175
Sep 20, 2025
-
80 Kg Woman
Sep 20, 2025
-
24 3 4
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X/3 - X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.