4 2x 1
interactiveleap
Sep 20, 2025 · 6 min read
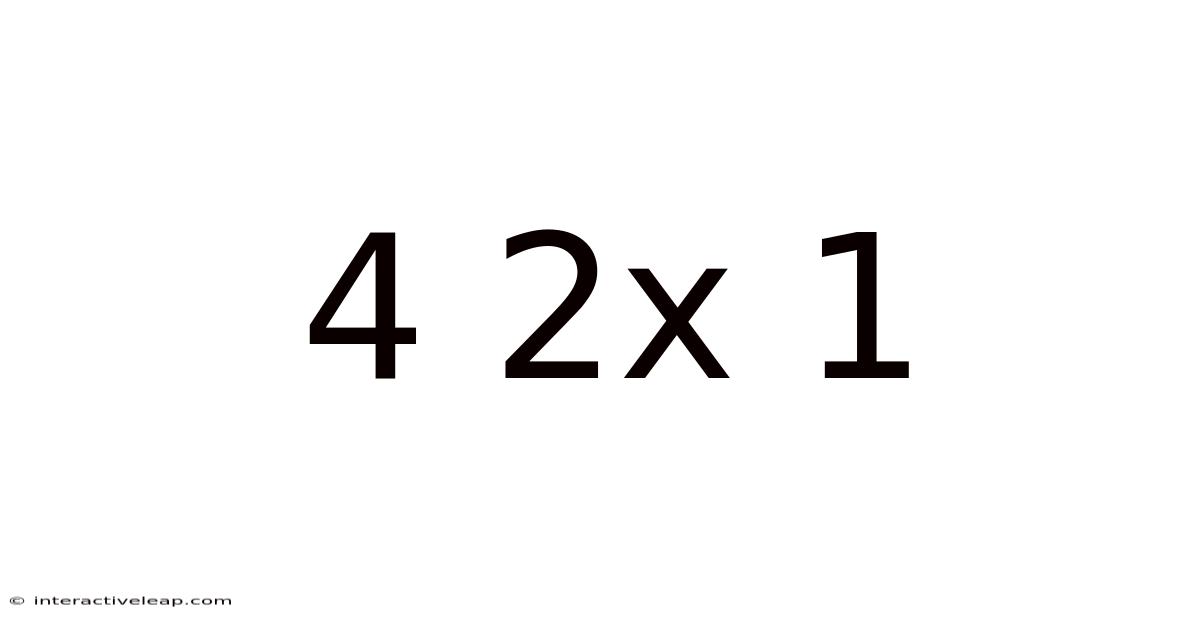
Table of Contents
Decoding 4 x 2 x 1: A Deep Dive into Multiplication, Factorials, and Their Applications
This article explores the seemingly simple mathematical expression "4 x 2 x 1," delving beyond its basic calculation to reveal its significance in various mathematical contexts, particularly within the realm of factorials and their practical applications. We'll unravel its meaning, explore its connection to permutations and combinations, and discuss its relevance in probability, statistics, and even computer science. Understanding 4 x 2 x 1 is a stepping stone to grasping more complex mathematical concepts.
Understanding the Basics: Multiplication
At its core, "4 x 2 x 1" represents a series of multiplications. Multiplication is a fundamental arithmetic operation signifying repeated addition. In this case, we're multiplying 4 by 2, resulting in 8, and then multiplying that result by 1, which leaves us with the final answer of 8. This simple calculation forms the bedrock of understanding more advanced concepts.
Introducing Factorials: The "!" Symbol
The expression "4 x 2 x 1" is, in fact, a concise representation of a factorial, denoted by the symbol "!". A factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. Therefore, "4 x 2 x 1" is equivalent to 4!, which is read as "4 factorial."
- 4! = 4 x 3 x 2 x 1 = 24
Notice the difference: While "4 x 2 x 1" equals 8, 4! (which includes the 3) equals 24. This seemingly small difference highlights the importance of paying close attention to mathematical notation. The omission or inclusion of a single number significantly alters the result.
Factorials in Permutations and Combinations
Factorials find their most prominent application in the fields of permutations and combinations – two fundamental concepts in probability and statistics.
-
Permutations: A permutation is an arrangement of objects in a specific order. If we have n distinct objects, the number of ways to arrange them in a row is given by n!. For example, if we have four distinct books (A, B, C, D), the number of ways to arrange them on a shelf is 4! = 24.
-
Combinations: Unlike permutations, combinations don't consider the order of objects. A combination is a selection of objects where the order doesn't matter. The number of ways to choose k objects from a set of n distinct objects is given by the combination formula: n! / (k! * (n-k)!). This formula utilizes factorials to calculate the number of possible combinations. For instance, if we want to choose 2 books out of 4, the number of combinations is 4! / (2! * 2!) = 6.
Applications in Probability and Statistics
Probability and statistics heavily rely on factorials for calculating probabilities involving arrangements and selections. Many probability distributions, such as the binomial distribution and the hypergeometric distribution, use factorials in their formulas. These distributions are crucial for modeling various real-world phenomena, including:
- Quality control: Determining the probability of finding a certain number of defective items in a sample.
- Genetics: Calculating the probability of inheriting specific genetic traits.
- Sports: Analyzing the probability of a team winning a series of games.
- Medical research: Assessing the effectiveness of a new drug or treatment.
Factorials and the Gamma Function: Extending Beyond Integers
While factorials are defined for non-negative integers, the Gamma function (Γ(z)) extends the concept of factorials to complex numbers. The Gamma function is a generalization of the factorial function, meaning it produces the same results for positive integers as the factorial, but it can also handle non-integer and complex inputs. This generalization is essential for advanced mathematical analysis and applications in various scientific fields. The relationship between the factorial and the Gamma function is:
n! = Γ(n+1) for n being a non-negative integer
Factorials in Computer Science: Algorithms and Data Structures
Factorials frequently appear in algorithms and data structures in computer science. They play a crucial role in:
- Sorting algorithms: Analyzing the complexity of algorithms like bubble sort or merge sort, which often involve factorial-like computations in their worst-case scenarios.
- Graph theory: Calculating the number of spanning trees in a graph, or the number of Hamiltonian cycles.
- Recursion: Factorials are often used as examples in illustrating recursive functions, a fundamental programming concept.
For instance, a recursive function to calculate n! would look like this (in pseudocode):
function factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
Beyond 4 x 2 x 1: Exploring Larger Factorials
Understanding 4 x 2 x 1 provides a foundation for exploring larger factorials. As the number increases, the factorial value grows incredibly quickly. For instance:
- 5! = 120
- 10! = 3,628,800
- 20! ≈ 2.43 x 10^18
This rapid growth highlights the importance of efficient computational methods for calculating large factorials, especially in applications requiring high precision. Approximation techniques, like Stirling's approximation, are often used to handle very large factorials without the need for exact calculation.
Stirling's Approximation: A Powerful Tool
Stirling's approximation provides a way to estimate the value of n! for large values of n. It's expressed as:
n! ≈ √(2πn) * (n/e)^n
This approximation becomes increasingly accurate as n grows larger, making it a valuable tool when dealing with factorials that are computationally expensive to calculate exactly.
Frequently Asked Questions (FAQ)
Q: What is the difference between 4 x 2 x 1 and 4!?
A: While 4 x 2 x 1 equals 8, 4! (4 factorial) is 4 x 3 x 2 x 1 = 24. The difference lies in the inclusion of the number 3 in the factorial calculation.
Q: Why are factorials important in probability?
A: Factorials are crucial in probability because they help count the number of possible arrangements (permutations) and selections (combinations) of items, which are essential for calculating probabilities of events.
Q: How can I calculate large factorials efficiently?
A: For extremely large factorials, exact calculation can be computationally expensive. Approximation methods like Stirling's approximation are commonly used to estimate their values.
Q: What is the Gamma function, and why is it important?
A: The Gamma function is a generalization of the factorial function, extending its definition beyond non-negative integers to complex numbers. This generalization is crucial for various advanced mathematical applications.
Conclusion
The seemingly simple expression "4 x 2 x 1" opens the door to a world of mathematical concepts, from fundamental arithmetic operations to the powerful tools of factorials, permutations, combinations, and their applications in probability, statistics, and computer science. By understanding this foundational concept, we gain insight into more complex mathematical structures and their real-world implications. The journey from a simple multiplication to the intricacies of the Gamma function illustrates the beauty and interconnectedness of mathematical ideas. The seemingly straightforward "4 x 2 x 1" serves as a powerful reminder of the depth and breadth hidden within seemingly simple mathematical expressions.
Latest Posts
Latest Posts
-
450cm In Feet
Sep 20, 2025
-
20 Of 440
Sep 20, 2025
-
One Eye Minion
Sep 20, 2025
-
Hell Ya Meaning
Sep 20, 2025
-
85 Of 25
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 4 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.