85 Of 25
interactiveleap
Sep 20, 2025 · 5 min read
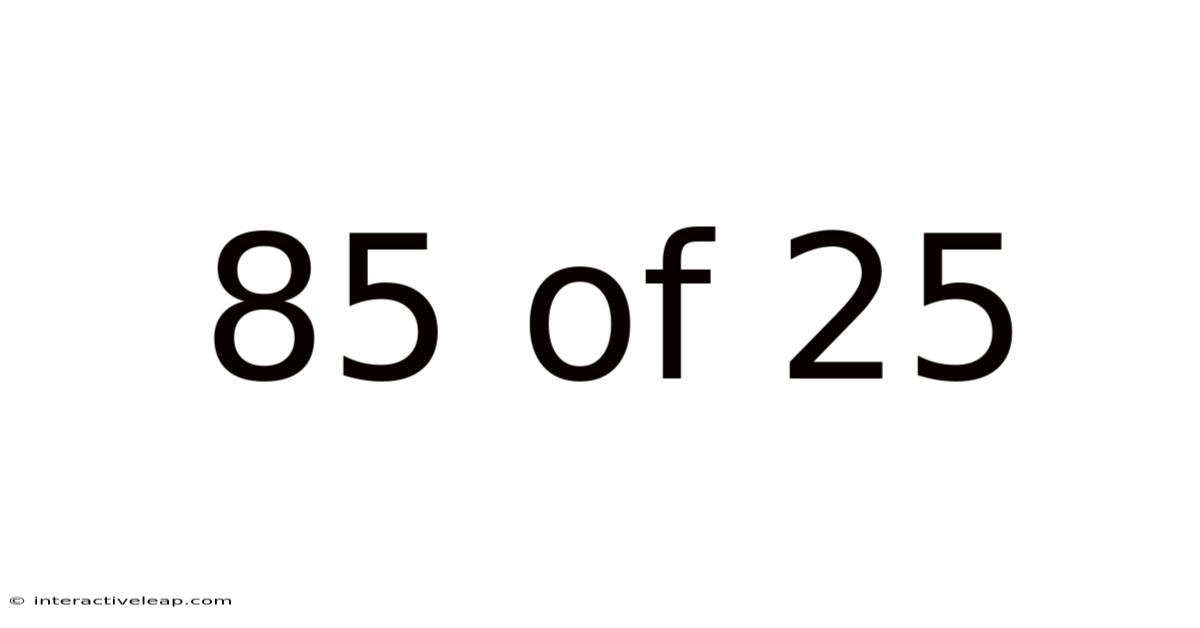
Table of Contents
Decoding the Fraction: A Deep Dive into 85/25
Understanding fractions is a fundamental building block in mathematics, essential for everything from basic arithmetic to advanced calculus. This article will explore the fraction 85/25 in detail, covering its simplification, decimal representation, percentage equivalent, and real-world applications. We'll also delve into the underlying concepts to solidify your understanding of fractions and their various forms. By the end, you'll not only know the answer to "What is 85/25?" but also possess a deeper understanding of fractional arithmetic.
Introduction to Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) indicates the whole is divided into four equal parts.
Simplifying the Fraction 85/25
The fraction 85/25 is not in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's find the GCD of 85 and 25. We can use the prime factorization method:
- Prime factorization of 85: 5 x 17
- Prime factorization of 25: 5 x 5
The common factor is 5. Therefore, the GCD of 85 and 25 is 5.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
85 ÷ 5 = 17 25 ÷ 5 = 5
Therefore, the simplified form of 85/25 is 17/5.
Converting to Decimal
To convert the simplified fraction 17/5 to a decimal, we perform the division:
17 ÷ 5 = 3.4
So, 85/25 is equal to 3.4 in decimal form.
Converting to Percentage
To convert the decimal 3.4 to a percentage, we multiply by 100:
3.4 x 100 = 340%
Therefore, 85/25 is equal to 340%. This indicates that 85 is 340% of 25.
Real-World Applications
Understanding fractions like 85/25 has practical applications in various fields:
- Finance: Calculating proportions of investments, interest rates, or discounts. For instance, if you invested $25 and earned a profit of $85, your return on investment would be 340%.
- Measurement: Dividing quantities, such as lengths, weights, or volumes. Imagine cutting a 25-meter rope into pieces of 85/25 meters.
- Cooking and Baking: Scaling recipes up or down. If a recipe calls for 25 grams of an ingredient and you want to make a larger batch requiring 85 grams, you're using a 340% scaling factor.
- Data Analysis: Representing proportions within datasets or calculating percentages of change.
Understanding Improper Fractions and Mixed Numbers
The fraction 17/5 is an improper fraction because the numerator (17) is greater than the denominator (5). Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction.
To convert 17/5 to a mixed number, we divide the numerator (17) by the denominator (5):
17 ÷ 5 = 3 with a remainder of 2
The quotient (3) becomes the whole number, and the remainder (2) becomes the numerator of the proper fraction, while the denominator remains the same (5). Therefore, 17/5 as a mixed number is 3 2/5.
Further Exploration: Working with Fractions
Let's explore some more concepts related to fractions:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
-
Multiplying Fractions: To multiply fractions, multiply the numerators together and multiply the denominators together. Simplify the resulting fraction if possible.
-
Dividing Fractions: To divide fractions, invert the second fraction (reciprocal) and multiply.
-
Equivalent Fractions: Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/2, 2/4, and 4/8 are all equivalent fractions.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 85/25?
A: The simplest form of 85/25 is 17/5.
Q: How do you convert 85/25 to a decimal?
A: Divide 85 by 25 to get 3.4.
Q: What is 85/25 as a percentage?
A: 85/25 is equal to 340%.
Q: Can 85/25 be expressed as a mixed number?
A: Yes, 85/25 (or its simplified form 17/5) can be expressed as the mixed number 3 2/5.
Q: What are some real-world applications of understanding this fraction?
A: Applications include financial calculations, measurements, cooking, and data analysis, as detailed above.
Conclusion
This in-depth analysis of the fraction 85/25 demonstrates the importance of understanding fundamental mathematical concepts. We’ve covered simplification, decimal and percentage conversions, real-world applications, and related fractional operations. Remember, mastering fractions is a crucial skill with far-reaching implications across numerous disciplines. By understanding the processes involved in simplifying, converting, and applying fractions like 85/25, you build a strong foundation for more advanced mathematical studies and real-world problem-solving. Continue practicing and exploring different fractional operations to further solidify your understanding.
Latest Posts
Latest Posts
-
Gi Scrabble Word
Sep 20, 2025
-
75 Of 7
Sep 20, 2025
-
My Daughter French
Sep 20, 2025
-
1 1 2 Tbsp
Sep 20, 2025
-
23 X 7
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.