23 X 7
interactiveleap
Sep 20, 2025 · 6 min read
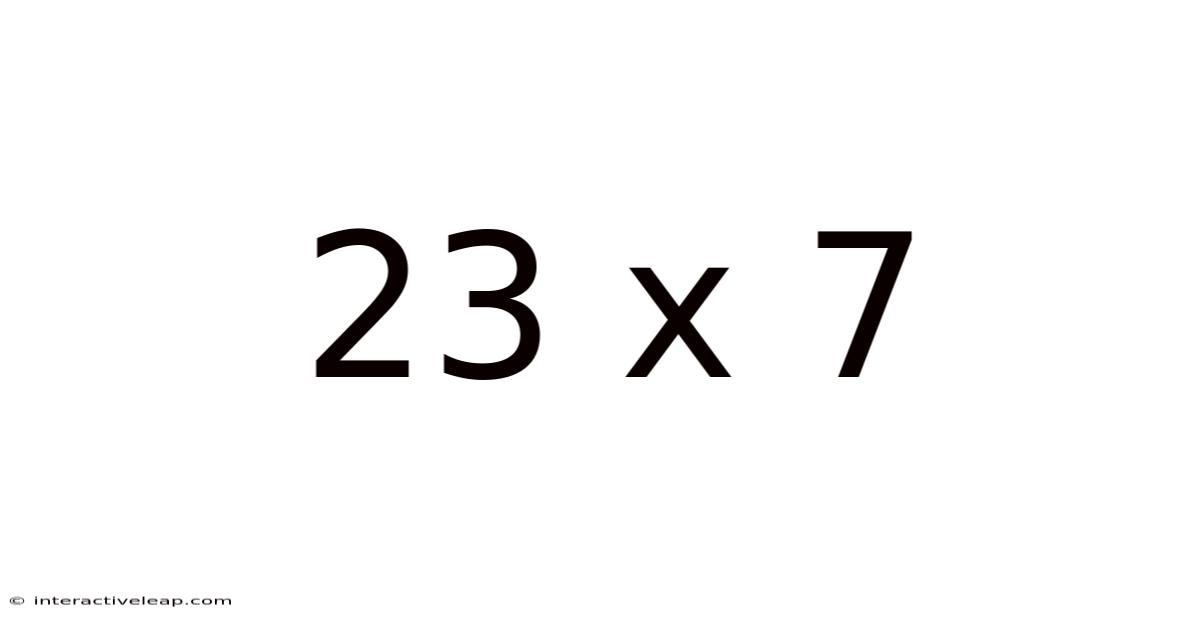
Table of Contents
Unpacking 23 x 7: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem of 23 x 7, expanding far beyond the immediate answer to delve into the underlying mathematical concepts, practical applications, and even some intriguing historical perspectives. Understanding this single calculation unlocks a world of mathematical knowledge, highlighting the beauty and power of numbers. We'll explore different methods of solving the problem, discuss the properties of multiplication, and look at how this seemingly basic operation forms the foundation of more complex mathematical principles.
Introduction: More Than Just an Answer
At first glance, 23 x 7 seems straightforward. A quick calculation reveals the answer: 161. However, this seemingly simple problem offers a rich opportunity to explore fundamental mathematical concepts, different calculation techniques, and their real-world applications. This exploration will benefit students, educators, and anyone curious about the fascinating world of numbers. We will examine various approaches to solving this multiplication, from traditional methods to more advanced techniques, emphasizing the underlying principles and demonstrating their versatility.
Method 1: The Standard Algorithm
The most common method taught in schools is the standard algorithm for multiplication. This involves breaking down the numbers into their place values (tens and ones) and performing the multiplication step-by-step.
- Multiply the ones: 7 x 3 = 21. Write down '1' and carry-over '2'.
- Multiply the tens: 7 x 2 = 14. Add the carry-over '2': 14 + 2 = 16. Write down '16'.
- Combine the results: The final answer is 161.
This method is effective for its simplicity and systematic approach, making it easily understandable for beginners. However, it's essential to understand why this method works, which involves a deep understanding of place value and the distributive property of multiplication.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this property to solve 23 x 7:
23 x 7 = (20 + 3) x 7 = (20 x 7) + (3 x 7) = 140 + 21 = 161
This method highlights the fundamental principle behind the standard algorithm. Breaking down the larger number into smaller, manageable components simplifies the calculation and makes it easier to grasp the underlying mathematical logic. This method is particularly helpful in understanding the conceptual basis of multiplication.
Method 3: Repeated Addition
Multiplication can be viewed as repeated addition. 23 x 7 is equivalent to adding 23 seven times:
23 + 23 + 23 + 23 + 23 + 23 + 23 = 161
While seemingly inefficient for larger numbers, this method reinforces the foundational relationship between addition and multiplication. It’s a useful visualization, especially for younger learners who are still developing their understanding of multiplication.
Method 4: Lattice Multiplication
Lattice multiplication, an ancient method, provides a visual and organized approach. It involves creating a grid, breaking down the numbers by place value, and performing individual multiplications within the grid. The results are then added diagonally. This method is less commonly used today but demonstrates a different perspective on the multiplication process and can be a valuable tool for developing number sense.
The Properties of Multiplication
Understanding the properties of multiplication is crucial to mastering this fundamental operation. These properties apply to 23 x 7 and all other multiplication problems:
- Commutative Property: The order of the numbers doesn't matter (23 x 7 = 7 x 23). This is a powerful property that simplifies calculations and enhances understanding.
- Associative Property: When multiplying more than two numbers, the grouping doesn't affect the result (e.g., (2 x 3) x 7 = 2 x (3 x 7)).
- Identity Property: Multiplying any number by 1 results in the same number (23 x 1 = 23).
- Zero Property: Multiplying any number by 0 results in 0 (23 x 0 = 0).
- Distributive Property: As already discussed, this property allows us to break down multiplication into simpler steps.
Real-World Applications of 23 x 7 (and Multiplication in General)
The seemingly simple calculation of 23 x 7 has numerous real-world applications, highlighting the practical relevance of mathematical skills:
- Calculating Costs: Imagine buying 23 items costing $7 each. The total cost is 23 x 7 = $161. This illustrates the everyday use of multiplication in personal finance.
- Measuring Areas: If a rectangular area measures 23 units by 7 units, the total area is 161 square units. This demonstrates the application of multiplication in geometry and measurement.
- Scaling Recipes: If a recipe calls for 7 units of an ingredient per serving, and you want to make 23 servings, you would need 23 x 7 units of that ingredient. This shows how multiplication is crucial in cooking and baking.
- Data Analysis: In various fields, from science to business, multiplication is fundamental to analyzing data, scaling values, and making calculations.
These examples showcase the widespread utility of multiplication, demonstrating its relevance beyond academic settings. Mastering this basic operation is crucial for success in many aspects of life.
Historical Context: The Evolution of Multiplication
Multiplication methods have evolved significantly over time. Ancient civilizations employed various techniques, including using tally marks, abacuses, and different forms of written notation. The development of algorithms and computational tools has further simplified the process, allowing us to solve complex multiplication problems with ease. Understanding the historical context highlights the continuous human effort to improve mathematical understanding and efficiency.
Advanced Concepts Related to 23 x 7
The seemingly simple 23 x 7 opens doors to more complex mathematical concepts:
- Prime Factorization: Both 23 and 7 are prime numbers (numbers divisible only by 1 and themselves). This introduces the concept of prime factorization, a fundamental concept in number theory.
- Modular Arithmetic: Exploring the remainder when 161 is divided by different numbers introduces the concept of modular arithmetic, a crucial component of cryptography and other advanced mathematical fields.
- Algebraic Representation: The problem can be represented algebraically as x = 23 * 7, introducing the concept of variables and equations.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes students make when multiplying numbers like 23 x 7?
- A: Common errors include incorrect carrying over of digits, misplacing digits in the answer, and not understanding the place value system. Careful attention to detail and practice are crucial for avoiding these mistakes.
-
Q: Are there any shortcuts or tricks to make multiplication faster?
- A: Yes, understanding the distributive property and practicing mental math techniques can significantly improve speed and efficiency. Learning multiplication tables by heart is also very beneficial.
-
Q: How can I help a child learn multiplication?
- A: Use visual aids, games, and real-world examples to make learning engaging. Start with smaller numbers and gradually increase the difficulty. Focus on understanding the underlying principles rather than rote memorization.
Conclusion: The Enduring Significance of 23 x 7
While the answer to 23 x 7 is simply 161, the journey to reach that answer has unveiled a wealth of mathematical knowledge. This seemingly simple problem serves as a gateway to understanding fundamental concepts, diverse calculation methods, and the vast applications of multiplication in our world. From the standard algorithm to the distributive property, from historical methods to modern applications, this exploration has emphasized the beauty and power of numbers and the enduring significance of this fundamental mathematical operation. It highlights the importance of not just finding the answer, but understanding the process and appreciating the mathematical principles that underpin it. By exploring this one problem, we have embarked on a journey that demonstrates the interconnectedness of mathematical concepts and their relevance in various fields. The true value lies not only in the answer itself but in the deeper understanding gained along the way.
Latest Posts
Latest Posts
-
Caco3 Hcl Reaction
Sep 20, 2025
-
Sasuke Uchiha Died
Sep 20, 2025
-
25 Off 39
Sep 20, 2025
-
Overhead Projector Paper
Sep 20, 2025
-
New And Improved
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 23 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.