X2 X 25
interactiveleap
Sep 20, 2025 · 6 min read
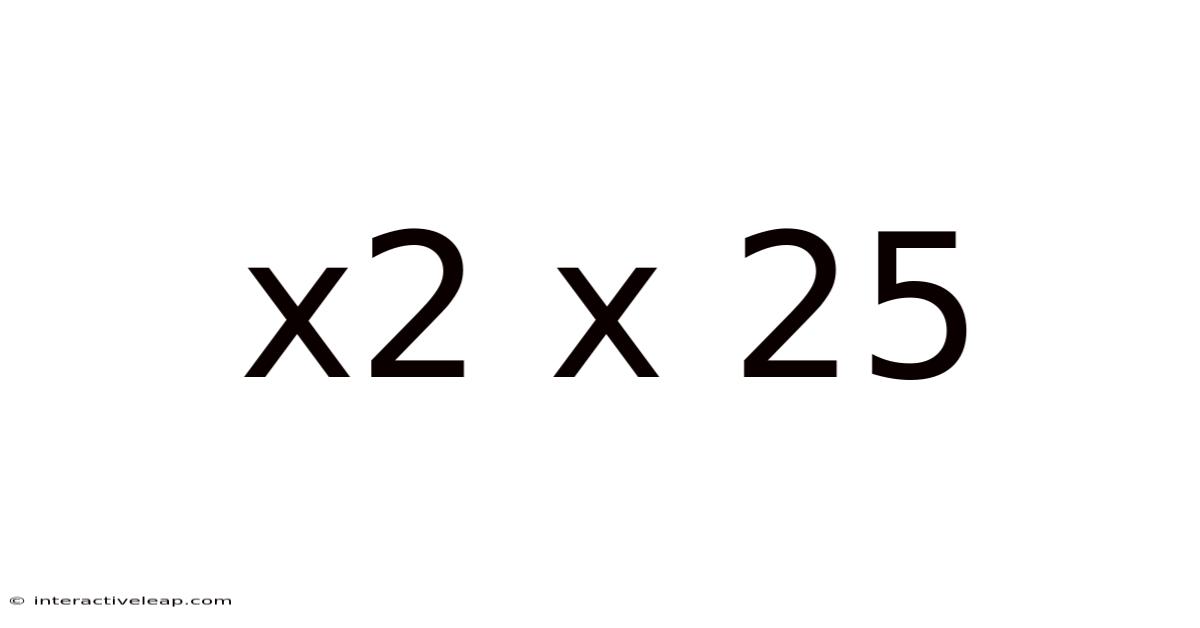
Table of Contents
Decoding X² x 25: Exploring Quadratic Equations and Their Applications
This article delves into the seemingly simple expression "x² x 25," unraveling its mathematical significance and exploring its applications in various fields. We'll move beyond a basic calculation to understand the underlying concepts of quadratic equations, their solutions, and their real-world relevance. This exploration will cover the fundamentals of algebra, delve into problem-solving techniques, and discuss the broader implications of this type of mathematical expression.
Understanding the Basics: Quadratic Equations
At its core, "x² x 25" represents a simplified form of a quadratic equation. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero.
In our case, "x² x 25" can be rewritten as a quadratic equation: x² - 25 = 0. Here, a = 1, b = 0, and c = -25. Notice the absence of the 'bx' term; this simplifies the solution process but doesn't diminish the importance of understanding the underlying principles.
Solving x² - 25 = 0: Factoring and the Difference of Squares
Solving this particular quadratic equation is relatively straightforward using the method of factoring. Specifically, we can utilize the difference of squares formula, which states that a² - b² = (a + b)(a - b).
In our equation, x² - 25 = 0, we can rewrite 25 as 5², giving us x² - 5² = 0. Applying the difference of squares formula, we get:
(x + 5)(x - 5) = 0
This equation is satisfied if either (x + 5) = 0 or (x - 5) = 0. Therefore, the solutions (or roots) of the equation are x = -5 and x = 5.
Graphical Representation: Parabolas and Roots
Quadratic equations are graphically represented by parabolas. A parabola is a U-shaped curve. The solutions to the quadratic equation, x = -5 and x = 5, represent the x-intercepts of the parabola – the points where the parabola intersects the x-axis.
The parabola representing x² - 25 = 0 opens upwards (because the coefficient of x² is positive). Its vertex (the lowest point) lies on the y-axis at (0, -25). Understanding the graphical representation provides a visual context for the solutions we found algebraically.
Beyond Factoring: The Quadratic Formula
While factoring is an efficient method for solving some quadratic equations, it's not always applicable. For more complex equations, the quadratic formula provides a universal solution:
x = [-b ± √(b² - 4ac)] / 2a
Applying this formula to our equation (x² - 25 = 0, where a = 1, b = 0, c = -25), we get:
x = [0 ± √(0² - 4 * 1 * -25)] / (2 * 1) x = ± √100 / 2 x = ± 10 / 2 x = ± 5
This confirms our earlier solutions: x = 5 and x = -5. The quadratic formula ensures we can solve any quadratic equation, regardless of its factorability.
The Discriminant: Unveiling the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. The discriminant provides valuable information about the nature of the roots:
- If b² - 4ac > 0: The equation has two distinct real roots (as in our example).
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has no real roots; the roots are complex numbers (involving the imaginary unit 'i').
For x² - 25 = 0, the discriminant is 0² - 4(1)(-25) = 100, which is greater than 0, indicating two distinct real roots.
Applications of Quadratic Equations: Real-World Examples
While seemingly abstract, quadratic equations have widespread applications in various fields:
-
Physics: Projectile motion, calculating the trajectory of a thrown object, is often modeled using quadratic equations. The height of the object over time follows a parabolic path.
-
Engineering: Designing bridges, arches, and other structures frequently involves quadratic equations to determine optimal shapes and stress distributions.
-
Economics: Quadratic functions are used in economic modeling to represent cost functions, revenue functions, and profit maximization problems.
-
Computer Graphics: Parabolas and other quadratic curves are fundamental elements in computer-aided design (CAD) and creating smooth curves in graphics.
-
Data Analysis: Quadratic regression models are used to fit quadratic curves to data sets, allowing for the prediction of future values based on trends.
Solving More Complex Quadratic Equations: Step-by-Step Guide
Let's consider a more complex example: 2x² + 5x - 3 = 0. We can't easily factor this equation, so we'll use the quadratic formula:
-
Identify a, b, and c: a = 2, b = 5, c = -3.
-
Substitute into the quadratic formula:
x = [-5 ± √(5² - 4 * 2 * -3)] / (2 * 2)
- Simplify:
x = [-5 ± √(25 + 24)] / 4 x = [-5 ± √49] / 4 x = [-5 ± 7] / 4
- Find the two solutions:
x₁ = (-5 + 7) / 4 = 2/4 = 0.5 x₂ = (-5 - 7) / 4 = -12/4 = -3
Therefore, the solutions to 2x² + 5x - 3 = 0 are x = 0.5 and x = -3.
Completing the Square: Another Solution Method
Another technique for solving quadratic equations is completing the square. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let’s illustrate this with the equation x² + 6x + 5 = 0:
-
Move the constant term to the right side: x² + 6x = -5
-
Take half of the coefficient of x (which is 6), square it (6/2 = 3, 3² = 9), and add it to both sides: x² + 6x + 9 = -5 + 9
-
Factor the left side as a perfect square: (x + 3)² = 4
-
Take the square root of both sides: x + 3 = ±2
-
Solve for x: x = -3 ± 2, which gives x = -1 and x = -5.
Frequently Asked Questions (FAQ)
Q: What if the quadratic equation has no real solutions?
A: If the discriminant (b² - 4ac) is negative, the quadratic equation has no real solutions. The solutions will be complex numbers involving the imaginary unit 'i'.
Q: Can I always solve a quadratic equation using factoring?
A: No. Factoring is only efficient for some quadratic equations. The quadratic formula or completing the square are more general methods that work for all quadratic equations.
Q: What is the significance of the vertex of a parabola?
A: The vertex represents the maximum or minimum value of the quadratic function. For parabolas that open upwards, the vertex is the minimum point, and for parabolas that open downwards, it's the maximum point.
Q: How can I determine if a parabola opens upwards or downwards?
A: The parabola opens upwards if the coefficient of x² (the 'a' in ax² + bx + c) is positive. It opens downwards if 'a' is negative.
Conclusion
The seemingly simple expression "x² x 25" opens a door to a vast world of mathematical concepts and real-world applications. By understanding quadratic equations, their various solution methods, and their graphical representation, we gain a powerful tool for modeling and solving problems across numerous disciplines. From calculating projectile trajectories to designing structures, the principles explored here are fundamental to many fields of study and practical applications. The ability to solve quadratic equations represents a crucial step in developing a deeper understanding of algebra and its relevance in the world around us. Mastering these concepts empowers you to tackle more complex mathematical problems and unlocks a greater appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
Opposite Of Highlight
Sep 20, 2025
-
4 2x 1
Sep 20, 2025
-
84 1kg In Stone
Sep 20, 2025
-
15 Of 175
Sep 20, 2025
-
80 Kg Woman
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X2 X 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.