63 Divided 3
interactiveleap
Sep 21, 2025 · 5 min read
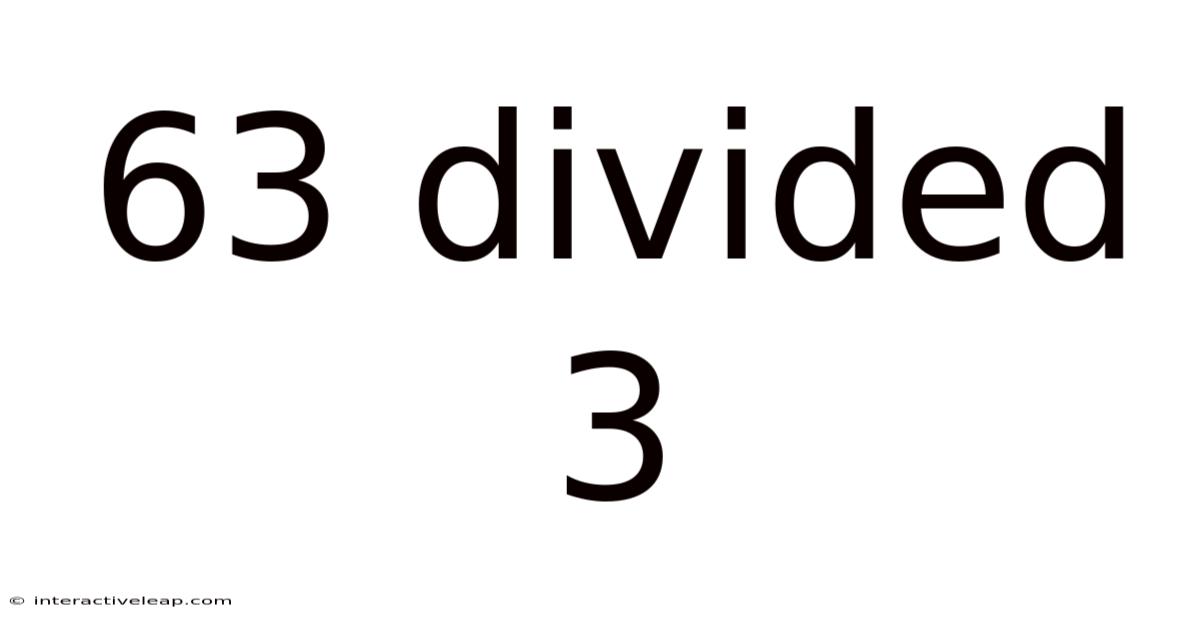
Table of Contents
Decoding Division: A Deep Dive into 63 Divided by 3
Dividing 63 by 3 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a rich opportunity to explore fundamental mathematical concepts and their practical applications. This article will not only provide the answer to 63 divided by 3 but will also delve into the underlying principles, explore different methods of solving the problem, and examine the broader context of division in mathematics. We'll also address common questions and misconceptions surrounding division.
Understanding Division: The Basics
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the inverse of multiplication. While multiplication combines groups of equal size, division separates a quantity into equal groups. The problem "63 divided by 3" asks: "How many times does 3 go into 63?" Or, equivalently, "If we divide 63 into 3 equal groups, how many will be in each group?"
The components of a division problem are:
- Dividend: The number being divided (63 in this case).
- Divisor: The number by which we are dividing (3 in this case).
- Quotient: The result of the division (the answer).
- Remainder: The amount left over if the dividend is not perfectly divisible by the divisor.
Methods for Solving 63 Divided by 3
Several methods can be used to solve 63 divided by 3. Let's explore a few:
1. Long Division:
This is a standard algorithm taught in schools.
21
3 | 63
-6
03
-3
0
We start by dividing 3 into the first digit of the dividend (6). 3 goes into 6 two times (2 x 3 = 6). We write the 2 above the 6. Then we subtract 6 from 6, leaving 0. We bring down the next digit (3). 3 goes into 3 one time (1 x 3 = 3). We write the 1 above the 3. Subtracting 3 from 3 leaves 0. Therefore, the quotient is 21, and the remainder is 0.
2. Repeated Subtraction:
This method involves repeatedly subtracting the divisor (3) from the dividend (63) until we reach 0. The number of times we subtract is the quotient.
63 - 3 = 60 60 - 3 = 57 57 - 3 = 54 54 - 3 = 51 51 - 3 = 48 48 - 3 = 45 45 - 3 = 42 42 - 3 = 39 39 - 3 = 36 36 - 3 = 33 33 - 3 = 30 30 - 3 = 27 27 - 3 = 24 24 - 3 = 21 21 - 3 = 18 18 - 3 = 15 15 - 3 = 12 12 - 3 = 9 9 - 3 = 6 6 - 3 = 3 3 - 3 = 0
We subtracted 3 a total of 21 times, confirming that 63 divided by 3 is 21. This method is conceptually simpler but can be time-consuming for larger numbers.
3. Multiplication:
Since division is the inverse of multiplication, we can find the answer by asking: "What number multiplied by 3 equals 63?" Through multiplication tables or mental math, we know that 3 x 21 = 63. Therefore, 63 divided by 3 is 21. This is often the quickest and most intuitive method for smaller numbers.
4. Using Factors:
We can break down the problem using the factors of 63. The prime factorization of 63 is 3 x 3 x 7. We can rewrite the division problem as: (3 x 3 x 7) / 3. One of the 3s cancels out, leaving 3 x 7 = 21.
The Answer: 63 Divided by 3 = 21
All the methods above consistently yield the same result: 63 divided by 3 equals 21. This means that if you divide 63 items into 3 equal groups, each group will contain 21 items.
Real-World Applications of Division
Division is a fundamental concept with numerous real-world applications across various fields:
- Sharing Equally: Dividing resources (candy, toys, money) among a group of people.
- Calculating Averages: Determining the average score on a test, average speed, or average temperature.
- Scaling Recipes: Adjusting ingredient quantities when cooking for a larger or smaller number of people.
- Unit Conversions: Converting between different units of measurement (e.g., meters to centimeters, pounds to ounces).
- Finance: Calculating interest rates, profit margins, and splitting bills.
- Engineering: Calculating dimensions, material quantities, and workload distribution.
Beyond the Basics: Exploring Division with Remainders
While 63 is perfectly divisible by 3, not all division problems result in a whole number quotient. Consider the problem 65 divided by 3.
Using long division:
21 R 2
3 | 65
-6
05
-3
2
Here, the quotient is 21, and the remainder is 2. This means that 65 can be divided into 3 groups of 21, with 2 items remaining. Understanding remainders is crucial in many real-world scenarios, such as determining how many buses are needed to transport a group of students (where each bus has a limited capacity).
Frequently Asked Questions (FAQs)
Q1: What if I divide by zero?
Dividing by zero is undefined in mathematics. It's a fundamental rule that you cannot divide by zero. Attempting to do so will result in an error.
Q2: How can I improve my division skills?
Practice is key! Regularly work through division problems of varying difficulty. Start with simpler problems and gradually increase the complexity. Utilize different methods to reinforce your understanding. Use flashcards or online resources for extra practice.
Q3: Are there any shortcuts for division?
For simple division problems, using multiplication tables or mental math can be a quick method. Understanding factors and prime factorization can also simplify certain divisions.
Q4: What are some common mistakes to avoid when dividing?
- Incorrect placement of digits: Pay close attention to digit placement during long division.
- Misinterpreting remainders: Understand the meaning and significance of remainders in the context of the problem.
- Dividing by zero: Always remember that division by zero is undefined.
Conclusion: More Than Just an Answer
The seemingly simple problem of 63 divided by 3 provides a gateway to understanding the broader world of mathematics. By exploring different solution methods and considering the real-world applications of division, we move beyond the mere calculation of the answer (21) and gain a deeper appreciation for the fundamental role division plays in our understanding and interaction with the world around us. From sharing resources fairly to calculating complex engineering designs, division remains an essential tool in our mathematical arsenal. The ability to grasp and apply this fundamental operation is crucial for success in numerous academic and professional pursuits. Remember that mastering mathematics is a journey, not a sprint; consistent practice and a willingness to explore different methods will undoubtedly enhance your mathematical abilities.
Latest Posts
Latest Posts
-
5 Of 125
Sep 21, 2025
-
3600mm In Metres
Sep 21, 2025
-
25 Off 29
Sep 21, 2025
-
Vita Mia Meaning
Sep 21, 2025
-
70 X 9
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 63 Divided 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.