5 Of 125
interactiveleap
Sep 21, 2025 · 6 min read
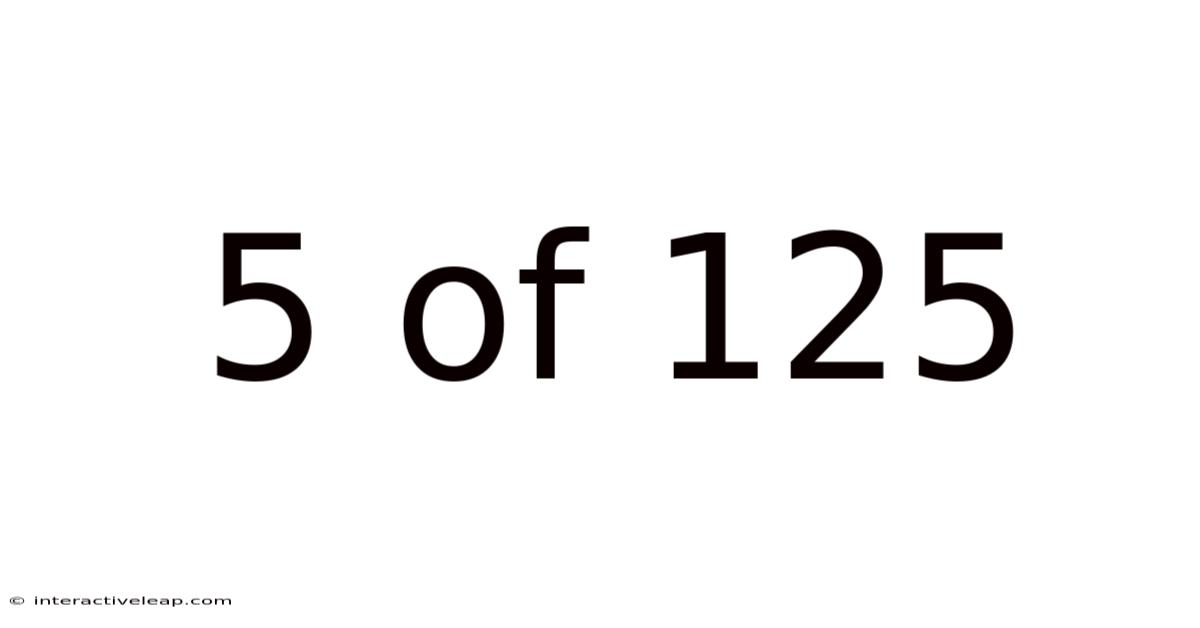
Table of Contents
Decoding the Enigma: Unveiling the Secrets Behind the 5 of 125 Phenomenon
The phrase "5 of 125" might initially seem cryptic, even nonsensical. However, it represents a fascinating concept within the realm of probability, statistics, and even philosophy, sparking curiosity and debate amongst mathematicians, statisticians, and anyone intrigued by the sheer randomness of life. This article delves deep into the meaning and implications of "5 of 125," exploring its significance across different contexts, from simple probability calculations to the philosophical implications of chance occurrences. We'll unpack the mathematics, address common misconceptions, and explore the surprising ways this seemingly insignificant ratio pops up in our everyday lives.
Understanding the Basic Probability
At its core, "5 of 125" represents a simple probability fraction: 5/125. This fraction simplifies to 1/25, or 4%. This seemingly small percentage holds significant weight when considering the likelihood of specific events occurring within a larger set of possibilities. The significance lies not in the absolute number, but in the context in which it's applied. Imagine a scenario where you're drawing marbles from a bag containing 125 marbles, 5 of which are red. The probability of drawing a red marble on your first try is 5/125, or 1/25. This is a fundamental concept in probability theory and serves as the bedrock for understanding more complex applications.
Beyond Simple Marbles: Real-World Applications
The 5/125 ratio, or its simplified form 1/25, transcends simple marble-drawing exercises. It appears subtly in various real-world scenarios:
-
Surveys and Sampling: Imagine conducting a survey of 125 people, and 5 respond with a specific answer. The 5/125 ratio allows you to calculate the percentage of respondents who gave that particular answer. This is crucial in statistical analysis, allowing researchers to draw inferences about a larger population based on a smaller sample.
-
Quality Control: In manufacturing, imagine inspecting 125 items, finding 5 defective. The 5/125 ratio directly indicates a 4% defect rate. This allows manufacturers to assess the effectiveness of their production processes and identify potential areas for improvement.
-
Medical Trials: In clinical trials, imagine 125 patients participating, with 5 experiencing a particular side effect. The 5/125 ratio, while seemingly small, contributes to the overall analysis of the drug's safety and efficacy. This information is critical in determining the risk-benefit profile of a medication.
The Mathematical Significance: Distributions and Expected Values
Understanding the 5/125 ratio often necessitates delving into statistical distributions. Depending on the context, different probability distributions might be relevant. For instance:
-
Binomial Distribution: If we're interested in the probability of getting exactly 5 red marbles when drawing 5 marbles with replacement from the bag of 125 (where the probability of drawing a red marble remains constant at 1/25), the binomial distribution is the appropriate tool. This distribution helps calculate the likelihood of obtaining a specific number of successes (red marbles) in a fixed number of trials.
-
Hypergeometric Distribution: If we're drawing marbles without replacement, the hypergeometric distribution becomes relevant. This distribution accounts for the fact that the probability of drawing a red marble changes with each draw. The fewer red marbles left in the bag, the lower the probability of drawing another one.
The concept of expected value is also crucial. In our marble example, the expected value of red marbles drawn in a single draw is simply (5/125) * 1 = 0.04. This means, on average, you'd expect to draw a red marble once every 25 draws.
Addressing Misconceptions and Common Errors
Several misconceptions surround probability and ratios like 5/125:
-
The Gambler's Fallacy: This fallacy assumes that past events influence future independent events. Just because you haven't drawn a red marble in the last 24 draws doesn't increase your chances of drawing one on the 25th draw. Each draw remains an independent event with a 1/25 probability.
-
Ignoring Sample Size: A small sample size can lead to misleading results. If only 5 out of 125 trials show a specific outcome, the results might not be statistically significant. Larger sample sizes generally provide more reliable estimates.
-
Confusing Probability with Certainty: A probability of 1/25 doesn't guarantee that a red marble will be drawn in 25 attempts. It's a measure of likelihood, not a guarantee.
The Philosophical Implications: Chance and Randomness
Beyond the mathematics, the 5/125 ratio touches on the philosophical aspects of chance and randomness. It reminds us that life is full of unpredictable events, some with seemingly small probabilities. However, these low-probability events still happen; they are not impossible.
This contemplation leads to deeper questions:
-
The Role of Chance in Shaping Events: To what extent do chance occurrences shape our lives and the world around us?
-
Predictability vs. Uncertainty: How can we reconcile our desire for predictability with the inherent uncertainty of many events?
-
The Significance of Rare Events: What is the significance of seemingly rare events (those with low probabilities) in a larger context?
The 5/125 ratio, while seemingly simple, can be a gateway to understanding fundamental concepts in probability, statistics, and even philosophy. Its applications are vast and varied, ranging from simple calculations to complex statistical analysis, and even prompting deeper philosophical reflections on chance and uncertainty in life.
Frequently Asked Questions (FAQ)
-
Q: Can I use this ratio in any context? A: While the basic probability calculation remains the same, the interpretation and applicability will vary depending on the specific situation. You must consider the relevant statistical distribution (binomial, hypergeometric, etc.) and sample size.
-
Q: How can I calculate the probability of NOT drawing a red marble? A: The probability of not drawing a red marble is simply 1 - (5/125) = 24/25, or 96%.
-
Q: What if I draw more than one marble? A: The calculation becomes more complex and requires considering either binomial or hypergeometric distribution, depending on whether you replace the marbles after each draw.
-
Q: Is a 4% chance considered significant? A: The significance of a 4% chance depends entirely on the context. In some cases, it might be considered negligible, while in others (e.g., medical side effects), it might be a crucial piece of information.
-
Q: What other ratios are similar in significance? A: Many ratios can be interpreted similarly, depending on the context. For instance, 1/10, 1/100, or even 1/1000 can be analyzed using the same probabilistic framework.
Conclusion
The seemingly simple ratio of 5 of 125, reducing to 1/25 or 4%, reveals a surprisingly rich world of mathematical concepts and philosophical considerations. Understanding its implications in probability, statistics, and various real-world applications empowers us to interpret data more effectively, make informed decisions, and appreciate the inherent randomness and unpredictability of life. While the numbers remain constant, the context and interpretation shift depending on the application. From quality control in manufacturing to the interpretation of clinical trial results, and even contemplating the role of chance in our lives, the 5 of 125 ratio serves as a powerful reminder of the intricate interplay between mathematics, probability, and the complexities of our world. Its simplicity belies its profound implications, making it a subject worthy of continued exploration and reflection.
Latest Posts
Latest Posts
-
7 7km In Miles
Sep 21, 2025
-
Burrow With Burrow
Sep 21, 2025
-
15 Of 21
Sep 21, 2025
-
15 Of 500
Sep 21, 2025
-
Katniss Flame Dress
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 5 Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.