15 Of 500
interactiveleap
Sep 21, 2025 · 5 min read
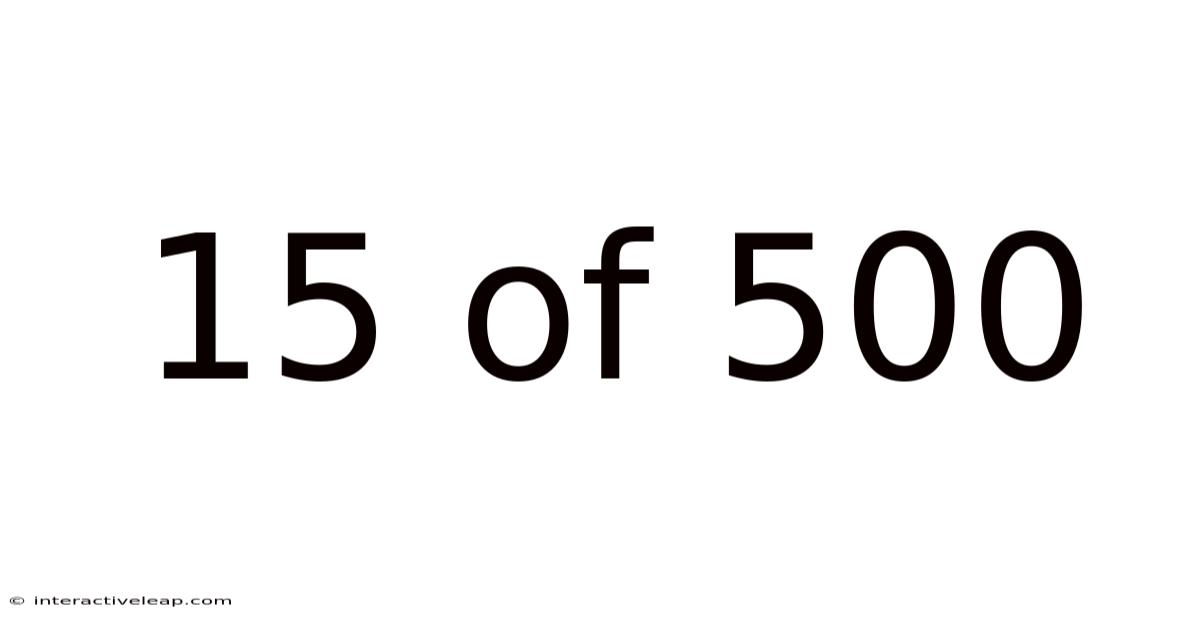
Table of Contents
Decoding 15 out of 500: Understanding Percentages, Fractions, and Their Real-World Applications
Understanding fractions and percentages is fundamental to navigating our daily lives. From calculating discounts at the mall to understanding statistical data in news reports, these concepts are essential tools for informed decision-making. This article delves deep into the meaning of "15 out of 500," exploring its representation as a fraction, a percentage, and its practical applications across various fields. We'll also tackle common misconceptions and provide clear, step-by-step explanations to enhance your understanding. By the end, you'll not only grasp the numerical significance of 15 out of 500 but also gain a broader understanding of proportional reasoning.
What Does "15 out of 500" Mean?
The phrase "15 out of 500" signifies a part-to-whole relationship. It means that 15 represents a portion of a larger whole consisting of 500 units. These units could be anything: apples, people, test scores, or even data points. The key is that 15 is a subset of the larger 500.
Representing "15 out of 500" as a Fraction
The most straightforward way to represent "15 out of 500" is as a fraction: 15/500. This fraction signifies that 15 is the numerator (the part) and 500 is the denominator (the whole). This fraction can be simplified by finding the greatest common divisor (GCD) of 15 and 500. The GCD of 15 and 500 is 5. Dividing both the numerator and the denominator by 5, we get the simplified fraction: 3/100. This simplified form is often easier to work with and understand.
Converting the Fraction to a Percentage
Percentages are simply fractions with a denominator of 100. Since our simplified fraction is already 3/100, converting it to a percentage is a straightforward process. 3/100 is equivalent to 3%. Therefore, 15 out of 500 is equal to 3%. This percentage representation provides a concise and readily understandable way to express the proportion.
Understanding Proportional Reasoning
The relationship between 15, 500, 3%, and the fraction 3/100 showcases the power of proportional reasoning. Proportional reasoning is the ability to understand and use the relationships between different quantities. In this case, we can establish a proportion:
15/500 = 3/100 = 0.03
This demonstrates that the ratio between the part (15) and the whole (500) remains constant, regardless of how we express it (fraction or decimal). This principle underpins numerous applications in diverse fields.
Real-World Applications of 15 out of 500 (or 3%)
The concept of 15 out of 500, or its equivalent 3%, finds practical application in numerous scenarios:
-
Statistics and Data Analysis: Imagine a survey of 500 people, where 15 responded positively to a particular question. The 3% positive response rate provides valuable insights into public opinion.
-
Quality Control: In a manufacturing process, if 15 out of 500 products are defective, the 3% defect rate can help identify areas for process improvement.
-
Financial Calculations: A 3% interest rate on a loan or investment is a common example. Understanding this percentage is crucial for making informed financial decisions.
-
Academic Performance: If a student answers 15 questions correctly out of 500 on a large exam, their performance can be expressed as 3%. This helps assess their understanding of the subject matter.
-
Scientific Research: In experimental studies, 3% might represent the success rate of a particular treatment or the prevalence of a specific characteristic within a sample population.
Beyond the Numbers: Interpreting the Context
While the numerical value of 3% is important, understanding the context is equally crucial. A 3% defect rate in a manufacturing process might be acceptable, while a 3% success rate in a medical treatment might be cause for concern. The significance of the percentage depends heavily on the specific application and the expectations surrounding it.
Common Misconceptions about Percentages and Fractions
-
Confusing Fractions and Percentages: While closely related, fractions and percentages are not interchangeable in every situation. Fractions represent a precise ratio, while percentages often involve rounding or approximation.
-
Incorrect Simplification of Fractions: Failure to simplify fractions can lead to inaccurate calculations and interpretations. Always aim to reduce fractions to their simplest form.
-
Misunderstanding Percentage Increases and Decreases: Percentage increases and decreases are not always additive or subtractive. A 10% increase followed by a 10% decrease does not result in the original value.
Step-by-Step Guide to Calculating Percentage from a Fraction
Let's break down the calculation process step-by-step, using the example of 15 out of 500:
-
Express as a Fraction: Write the given information as a fraction: 15/500.
-
Simplify the Fraction: Find the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 15 and 500 is 5. Divide both the numerator and denominator by 5 to get the simplified fraction: 3/100.
-
Convert to Percentage: Since percentages are fractions with a denominator of 100, the simplified fraction 3/100 directly translates to 3%.
Frequently Asked Questions (FAQs)
Q: How do I calculate the percentage if the denominator is not 100?
A: To calculate the percentage when the denominator is not 100, you need to convert the fraction to an equivalent fraction with a denominator of 100. You can do this by setting up a proportion or by dividing the numerator by the denominator and then multiplying by 100.
Q: What if I have a decimal instead of a fraction?
A: To convert a decimal to a percentage, simply multiply the decimal by 100 and add the % symbol. For example, 0.03 x 100 = 3%, which is equivalent to 3/100.
Q: How do I calculate the percentage change between two values?
A: To calculate the percentage change, subtract the original value from the new value, divide the result by the original value, and then multiply by 100.
Conclusion: Mastering the Fundamentals of Proportions
Understanding the concept of "15 out of 500," and its representation as a fraction (3/100) and a percentage (3%), is a fundamental skill with widespread practical applications. By mastering the principles of proportional reasoning and fraction simplification, you equip yourself with powerful tools for analyzing data, making informed decisions, and confidently navigating the numerical world around you. The seemingly simple calculation of 3% holds significant weight in various fields, highlighting the importance of grasping basic mathematical concepts for success in diverse areas of life. Remember to always consider the context in which these numbers are used to fully understand their meaning and implications.
Latest Posts
Latest Posts
-
Bebo In Spanish
Sep 21, 2025
-
91 52 X 5
Sep 21, 2025
-
450 3
Sep 21, 2025
-
Market Forces Meaning
Sep 21, 2025
-
N Size Battery
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.