70 X 9
interactiveleap
Sep 21, 2025 · 5 min read
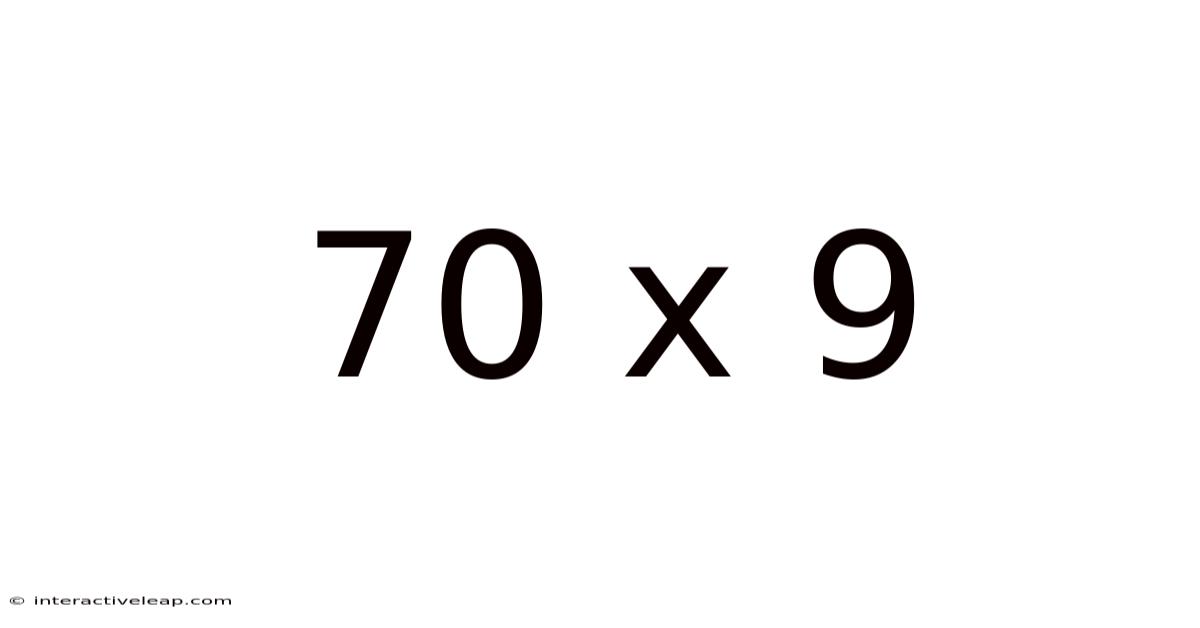
Table of Contents
Exploring the Multifaceted World of 70 x 9: From Basic Multiplication to Real-World Applications
This article delves into the seemingly simple calculation of 70 x 9, exploring its various facets, from the fundamental mathematical principles to its practical applications in diverse fields. We'll unravel the mystery behind this seemingly straightforward equation, revealing its hidden depths and demonstrating its relevance beyond the classroom. Understanding 70 x 9 isn't just about getting the right answer; it's about grasping the underlying concepts and appreciating its broader significance. This exploration is suitable for students, educators, and anyone curious about the power of mathematics in everyday life.
Understanding the Fundamentals: Multiplication and its Properties
Before diving into 70 x 9, let's refresh our understanding of multiplication. Multiplication is a fundamental arithmetic operation representing repeated addition. For example, 70 x 9 means adding 70 to itself nine times: 70 + 70 + 70 + 70 + 70 + 70 + 70 + 70 + 70. The result is the product of the two numbers, known as the multiplicand (70) and the multiplier (9).
Several key properties govern multiplication:
- Commutative Property: The order of the numbers doesn't affect the product. 70 x 9 is the same as 9 x 70.
- Associative Property: When multiplying multiple numbers, the grouping doesn't affect the product. This property is particularly relevant when dealing with more complex calculations involving 70 x 9 as part of a larger equation.
- Distributive Property: This allows us to break down complex multiplications into simpler ones. We can use this to solve 70 x 9 by breaking 70 into 7 x 10, making the calculation (7 x 10) x 9 = 7 x (10 x 9) = 7 x 90 = 630. This is a powerful technique for simplifying calculations, especially with larger numbers.
- Identity Property: Multiplying any number by 1 results in the same number. This seemingly trivial property is fundamental to many mathematical operations.
Solving 70 x 9: Different Approaches
There are several ways to solve 70 x 9, each illustrating a different mathematical concept:
1. Direct Multiplication: The simplest approach is to perform the multiplication directly. This can be done using a calculator or by applying the standard multiplication algorithm:
70
x 9
----
630
2. Breaking Down the Numbers (Distributive Property): As mentioned earlier, we can utilize the distributive property to simplify the calculation:
70 x 9 = (70 x 10) - (70 x 1) = 700 - 70 = 630
This approach showcases the power of breaking down complex problems into smaller, manageable parts.
3. Using Multiplication Tables: Familiarity with multiplication tables is crucial for efficient calculation. Knowing that 7 x 9 = 63 immediately gives us the answer, as 70 x 9 is simply 7 x 9 x 10 = 630.
4. Mental Math Techniques: With practice, one can develop efficient mental math techniques. For example, recognizing that 70 x 9 is the same as 7 x 9 with an added zero helps in quick mental calculation. Rounding and compensation techniques can also be used.
Beyond the Calculation: Real-World Applications
While 70 x 9 might seem like a simple mathematical problem, its applications extend far beyond the confines of a classroom. Consider these examples:
- Business and Finance: Calculating revenue from selling 70 items at $9 each.
- Engineering and Design: Determining the total length of 70 components, each measuring 9 units.
- Construction and Architecture: Calculating the area of a rectangular space with dimensions of 70 units by 9 units.
- Everyday Life: Determining the total cost of 70 items priced at $9 each or calculating the total number of minutes in 70 periods of 9 minutes each.
- Data Analysis and Statistics: When working with data sets, calculations similar to 70 x 9 might be used repeatedly.
These examples highlight the ubiquitous nature of multiplication and the relevance of seemingly simple calculations like 70 x 9 in various fields.
Expanding the Concept: Exploring Related Calculations
Understanding 70 x 9 helps build a foundation for understanding related calculations. For instance, it allows for easy calculation of:
- Multiples of 70 x 9: 140 x 9 (double 70 x 9), 210 x 9 (triple 70 x 9), and so on.
- Calculations involving similar numbers: 71 x 9, 69 x 9, 70 x 8, and 70 x 10.
- Calculations with fractions and decimals: 70 x 9.5, 70 x 0.9, etc.
The Importance of Mathematical Fluency
The ability to perform calculations like 70 x 9 efficiently and accurately is crucial for developing mathematical fluency. Mathematical fluency is more than just knowing the answer; it involves understanding the underlying concepts, applying different strategies, and solving problems with efficiency and accuracy. This fluency is essential for success in various academic and professional fields.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to solve 70 x 9?
- A: The quickest way depends on individual preferences and familiarity with multiplication tables. Direct multiplication, using the distributive property, or relying on memorized multiplication facts are all efficient methods.
-
Q: How can I improve my multiplication skills?
- A: Practice is key. Regularly practicing multiplication problems, using flashcards, and engaging in mental math exercises will significantly improve your speed and accuracy.
-
Q: Are there any online resources to help me practice multiplication?
- A: Many online resources offer interactive multiplication games and practice exercises. These resources can be invaluable for building multiplication skills.
-
Q: Why is it important to understand the properties of multiplication?
- A: Understanding the properties of multiplication allows for efficient and flexible problem-solving. It enables you to break down complex problems into simpler parts, choose the most suitable approach for a given problem, and develop a deeper understanding of mathematical concepts.
Conclusion: The Enduring Relevance of 70 x 9
The seemingly simple calculation of 70 x 9 provides a valuable opportunity to explore fundamental mathematical principles, practice different calculation strategies, and appreciate the broad applicability of mathematics in everyday life. Mastering this calculation is not just about getting the right answer (630); it's about developing a deeper understanding of multiplication, building mathematical fluency, and appreciating the power of mathematics to solve real-world problems. The skills acquired through understanding and practicing this calculation are transferable and valuable across various academic and professional fields. From business to engineering, from everyday life to advanced mathematical concepts, the ability to efficiently solve problems like 70 x 9 is a testament to the practical utility and enduring relevance of fundamental mathematical skills.
Latest Posts
Latest Posts
-
15 Of 500
Sep 21, 2025
-
Katniss Flame Dress
Sep 21, 2025
-
Electric Motor 3000w
Sep 21, 2025
-
Explain Limiting Reactant
Sep 21, 2025
-
54cm In Mm
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 70 X 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.