60 Of 220
interactiveleap
Sep 21, 2025 · 5 min read
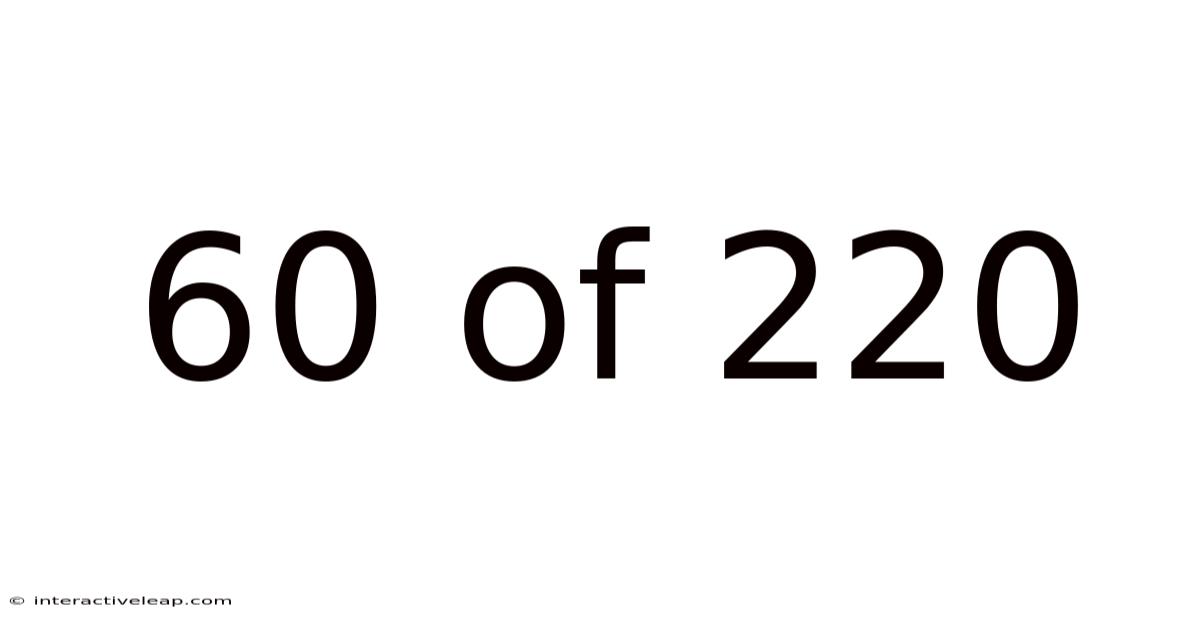
Table of Contents
Decoding the Fraction: Understanding 60/220 and its Implications
This article delves into the seemingly simple fraction 60/220, exploring its simplification, practical applications, and the broader mathematical concepts it represents. We'll go beyond basic arithmetic to uncover its significance in various fields, from everyday calculations to more complex mathematical analyses. Understanding fractions like 60/220 is crucial for building a solid foundation in mathematics and its practical applications.
Introduction: The Significance of Fraction Simplification
The fraction 60/220, at first glance, might seem straightforward. However, understanding its simplified form and the process behind it reveals fundamental principles in mathematics. Simplifying fractions is not merely about aesthetics; it's about finding the most efficient and concise representation of a given ratio. This process, also known as reducing a fraction to its lowest terms, improves clarity and simplifies calculations, making it easier to grasp the underlying relationships between numbers. This article will guide you through the process of simplifying 60/220 and explore its implications in various contexts.
Simplifying 60/220: A Step-by-Step Guide
The core principle of simplifying fractions lies in finding the greatest common divisor (GCD) of the numerator (60) and the denominator (220). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Let's find the GCD of 60 and 220 using the prime factorization method:
-
Prime Factorization of 60: 60 = 2 x 2 x 3 x 5 = 2² x 3 x 5
-
Prime Factorization of 220: 220 = 2 x 2 x 5 x 11 = 2² x 5 x 11
-
Identifying Common Factors: Both 60 and 220 share the factors 2² and 5.
-
Calculating the GCD: The GCD is the product of the common factors: 2² x 5 = 20
-
Simplifying the Fraction: Divide both the numerator and the denominator by the GCD (20):
60 ÷ 20 = 3 220 ÷ 20 = 11
Therefore, the simplified form of 60/220 is 3/11.
Alternative Methods for Finding the GCD
While prime factorization is a reliable method, other techniques can also be used to find the GCD, including:
-
Euclidean Algorithm: This iterative method involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD. For 60 and 220:
- 220 ÷ 60 = 3 with a remainder of 40
- 60 ÷ 40 = 1 with a remainder of 20
- 40 ÷ 20 = 2 with a remainder of 0
The GCD is 20.
-
Listing Factors: This method involves listing all the factors of both numbers and identifying the largest common factor. While simple for smaller numbers, it becomes less efficient for larger numbers.
Practical Applications of 60/220 and its Simplified Form (3/11)
The fraction 60/220, and its simplified equivalent 3/11, has practical applications in various scenarios:
-
Ratio and Proportion: Imagine a scenario where 60 out of 220 students in a school participate in a sports event. The fraction 60/220 represents the ratio of participating students to the total number of students. Simplifying this to 3/11 provides a clearer and more concise representation of this ratio.
-
Percentage Calculation: To express 60/220 as a percentage, we can use the simplified fraction: (3/11) x 100% ≈ 27.27%. This indicates that approximately 27.27% of the students participated in the event.
-
Probability: If there are 220 equally likely outcomes, and 60 of them represent a specific event, then the probability of that event occurring is 60/220, or its simplified form, 3/11.
-
Scaling and Measurement: In various engineering and architectural applications, scaling models often involve ratios. Understanding and simplifying fractions like 60/220 is crucial for accurate scaling.
Understanding Decimal Equivalents and Percentage Representation
The simplified fraction 3/11 can also be expressed as a decimal and a percentage:
-
Decimal Equivalent: To convert 3/11 to a decimal, we perform the division: 3 ÷ 11 ≈ 0.2727 (the 27 repeats infinitely).
-
Percentage Representation: As calculated earlier, 3/11 represents approximately 27.27%.
Beyond Simplification: Exploring Mathematical Concepts
The seemingly simple fraction 60/220 opens doors to more complex mathematical concepts:
-
Rational Numbers: Fractions like 60/220 are rational numbers, which can be expressed as a ratio of two integers. Understanding rational numbers is fundamental to algebra and other advanced mathematical topics.
-
Continued Fractions: Rational numbers can be represented as continued fractions. While beyond the scope of this basic introduction, exploring the continued fraction representation of 3/11 provides insights into number theory.
-
Approximations and Error Analysis: When dealing with decimal approximations, understanding the inherent error is crucial. The approximation of 3/11 as 0.2727 introduces a small error, which is important to consider in applications requiring high precision.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 60/220?
A: The simplest form of 60/220 is 3/11.
Q: How do I simplify a fraction in general?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both by the GCD.
Q: What are some methods to find the GCD?
A: Prime factorization, the Euclidean algorithm, and listing factors are common methods.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes calculations easier, improves clarity, and provides a more concise representation of a ratio.
Q: Can all fractions be simplified?
A: No. Fractions where the numerator and denominator have no common factors other than 1 are already in their simplest form. These are often called irreducible fractions.
Conclusion: Mastering Fractions – A Building Block for Mathematical Proficiency
Understanding fractions like 60/220 is a cornerstone of mathematical literacy. The process of simplifying fractions, while seemingly basic, underpins more complex mathematical concepts and has widespread applications in various fields. Mastering this skill builds a strong foundation for tackling more advanced mathematical problems and enhances problem-solving abilities in numerous real-world scenarios. By understanding the underlying principles and techniques, you can confidently approach and interpret fractional values, making you a more proficient and informed mathematician. The journey from 60/220 to its simplified form, 3/11, showcases the elegance and power of mathematical simplification.
Latest Posts
Latest Posts
-
1 73m In Inches
Sep 21, 2025
-
15 Of 80000
Sep 21, 2025
-
118pounds In Kg
Sep 21, 2025
-
1 5 X 7
Sep 21, 2025
-
Long Division Question
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.