15 Of 80000
interactiveleap
Sep 21, 2025 · 6 min read
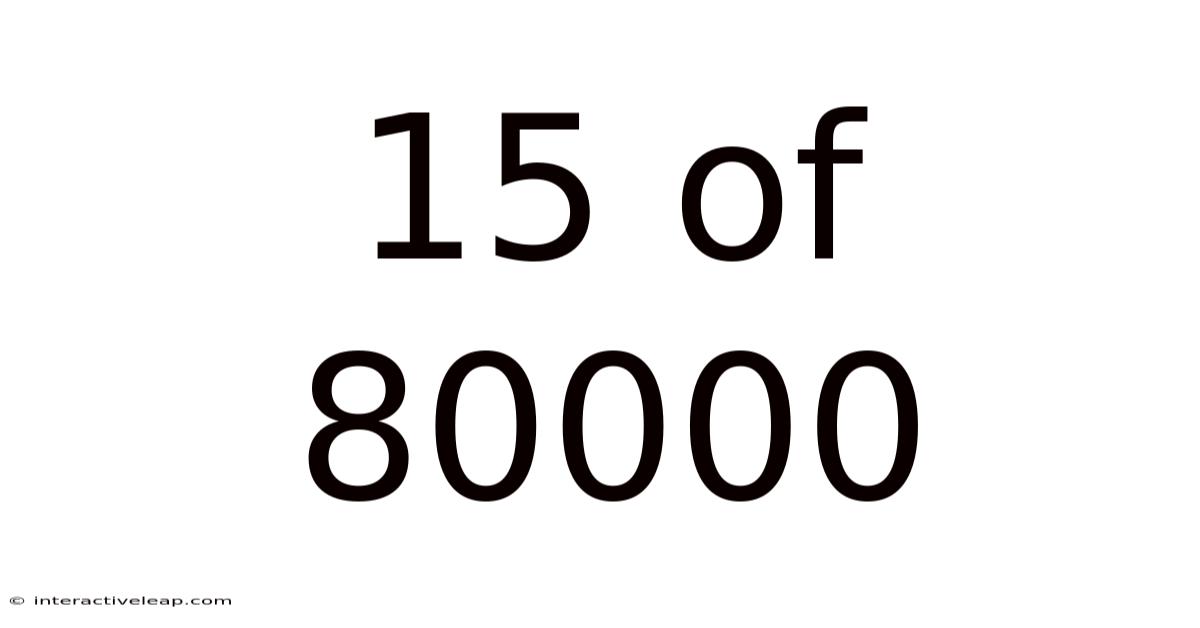
Table of Contents
Unveiling the Significance of 15 out of 80,000: A Deep Dive into Probability, Statistics, and Real-World Applications
Understanding the seemingly insignificant fraction of 15 out of 80,000 requires more than just a simple calculation. It involves delving into the world of probability, statistics, and their diverse applications in various fields. This article will explore the meaning behind this ratio, explaining its implications and illustrating its relevance through real-world examples. We will examine how this small percentage can hold significant weight depending on context, ranging from clinical trials to lottery odds. Prepare to be surprised by the depth of meaning hidden within these seemingly simple numbers.
Understanding the Basic Calculation
At its core, 15 out of 80,000 represents a fraction: 15/80000. This can be simplified to approximately 0.0001875, or 0.01875%. This percentage signifies that 15 represents a very small portion of the total 80,000. While the raw number seems minuscule, its interpretation and significance depend heavily on the context in which it appears.
The Importance of Context: Where 15/80000 Matters
The true value of understanding 15 out of 80,000 lies in appreciating the context. A small percentage in one scenario might be incredibly significant in another. Let’s explore a few examples:
-
Clinical Trials: Imagine a new drug undergoing clinical trials. If 15 out of 80,000 participants experienced a serious adverse reaction, this seemingly small percentage might be alarming. Pharmaceutical companies and regulatory bodies scrutinize even small adverse event rates, as the potential for harm to a large population needs to be considered. A seemingly insignificant percentage translates to a significant number of individuals affected when scaled to millions of potential users. This necessitates a thorough investigation into the root cause of these reactions and potentially halting the drug's development or adjusting its usage guidelines.
-
Lottery Odds: In contrast, consider a lottery with 80,000 possible winning combinations. If only 15 tickets match the winning numbers, the odds of winning are extremely low. While the raw percentage is the same, the context shifts the meaning. The low probability reinforces the idea of a lottery as a game of chance, where the likelihood of winning is slim, even if 15 people do, in fact, win.
-
Defect Rate in Manufacturing: In a manufacturing process, 15 defective units out of 80,000 might represent an acceptable defect rate, depending on industry standards and the cost of correcting the defects. However, even a small defect rate can have a significant financial impact when multiplied across large production runs. Quality control measures are crucial for minimizing defects, even if the percentage seems insignificant initially.
-
Rare Disease Prevalence: If 15 cases of a rare disease are identified in a population of 80,000, this low prevalence doesn’t diminish the severity of the condition for those affected. Epidemiologists use such data to track disease patterns, understand risk factors, and develop strategies for prevention and treatment, even if the overall prevalence is exceptionally low.
-
Environmental Monitoring: In environmental monitoring, 15 instances of a specific pollutant exceeding safety limits out of 80,000 samples could signal a localized environmental problem. While seemingly small, it necessitates investigation to pinpoint the source and prevent further contamination.
Statistical Significance: Beyond the Numbers
Moving beyond the raw percentage, we need to consider the concept of statistical significance. This involves determining whether the observed result (15 out of 80,000) is likely due to chance or reflects a real underlying effect. Statistical tests, like the chi-squared test or Fisher's exact test, are used to assess this.
The statistical significance depends on several factors:
- Sample size: A larger sample size (more than 80,000) would provide more reliable results.
- Expected value: What was the expected rate of the event (e.g., defective units, adverse reactions)? A significant deviation from the expected value might indicate a real effect.
- Significance level (alpha): This is the probability of rejecting the null hypothesis (that there's no real effect) when it's actually true. A common significance level is 0.05 (5%).
Applying Probability Theory
Probability theory allows us to quantify the likelihood of observing 15 events out of 80,000 given a certain probability of the event occurring in a single trial. This can be modeled using the binomial distribution, assuming each event is independent. However, the complexity of calculating the binomial probability for these specific numbers makes it more practical to use statistical software or approximation methods like the normal distribution. The key takeaway is that the probability of observing 15 events (or a higher number) would depend on the underlying probability of the event and will help determine whether the observed number is statistically significant or just random chance.
Practical Applications and Case Studies
Let's delve into a few hypothetical case studies to illustrate the real-world application of understanding 15 out of 80,000:
Case Study 1: A New Vaccine's Efficacy
A new vaccine is being tested. Out of 80,000 participants, 15 contracted the disease despite receiving the vaccine. Is the vaccine effective? This requires comparing the 15 cases to a control group that didn't receive the vaccine. If the control group had a much higher infection rate, the vaccine might still be considered effective, despite the 15 cases. The percentage alone doesn't tell the whole story.
Case Study 2: Manufacturing Defects in Electronics
A factory produces 80,000 electronic components daily. 15 are found to be defective. Is this acceptable? This depends on industry standards, cost of repair, and the potential consequences of a defective component. A higher cost associated with a faulty component might mean even 15 defects are too many, necessitating adjustments to the manufacturing process.
Case Study 3: Environmental Pollution
Water samples from a lake are taken. Out of 80,000 tests, 15 show high levels of a specific pollutant. Is this cause for concern? Yes, this requires immediate investigation to identify the source of the pollution and implement corrective measures. The small percentage doesn't diminish the environmental risk.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage represented by 15 out of 80,000?
A: Simply divide 15 by 80,000 and multiply by 100%: (15/80000) * 100% ≈ 0.01875%.
Q: Is 15 out of 80,000 statistically significant?
A: This depends entirely on the context. Statistical significance is determined using statistical tests and considering factors like the expected rate, sample size, and significance level. It is not inherently significant or insignificant.
Q: What are some other real-world applications of this concept?
A: Many fields use this type of analysis, including medicine (adverse effects), quality control (defect rates), finance (risk assessment), and environmental science (pollution monitoring).
Conclusion: The Bigger Picture
Understanding the meaning of 15 out of 80,000 requires moving beyond a simple numerical calculation. It necessitates understanding the context in which this ratio arises and applying the principles of probability and statistics to determine its true significance. The seemingly small percentage can hold considerable weight depending on the situation, highlighting the importance of careful analysis and consideration of the bigger picture. Whether it's a critical issue in a clinical trial or a manageable defect rate in manufacturing, the context dictates the true implications of this seemingly insignificant fraction. A deep dive into statistical analysis is crucial for proper interpretation and informed decision-making. The ability to analyze and interpret such data is a crucial skill across diverse fields. Remember, the seemingly small can hold immense significance when viewed through the right lens.
Latest Posts
Latest Posts
-
10 Of 1100
Sep 21, 2025
-
Rdm Meaning Gta
Sep 21, 2025
-
Antonyms For Reservoir
Sep 21, 2025
-
35 Of 15
Sep 21, 2025
-
18 5 6
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 80000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.