6 2x 3
interactiveleap
Sep 20, 2025 · 6 min read
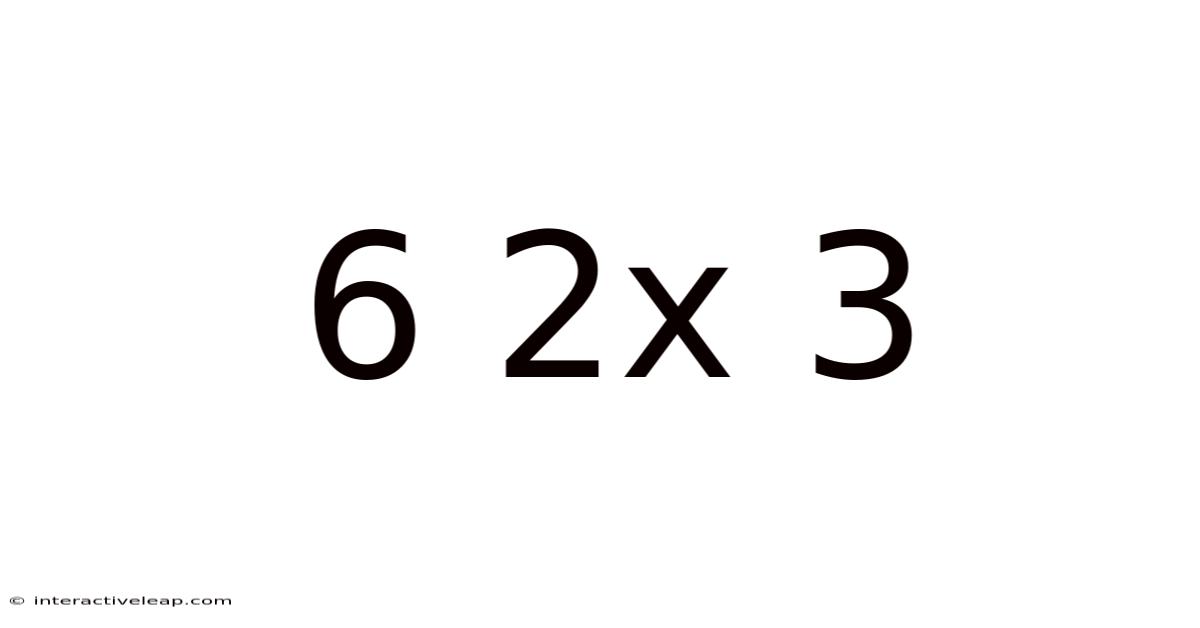
Table of Contents
Decoding 6 x 2 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "6 x 2 x 3," delving beyond the basic answer to uncover the underlying principles of multiplication, its various applications in real-world scenarios, and its significance in broader mathematical concepts. We'll unravel the process, examine different approaches to solving it, and explore its relevance in fields ranging from everyday calculations to advanced mathematical modeling. Understanding this seemingly simple equation unlocks a deeper comprehension of fundamental mathematical operations.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a shortcut for repeated addition. The expression "6 x 2 x 3" can be interpreted as:
- 6 added to itself 2 times, then the result is multiplied by 3.
Alternatively, we can think of it as:
- 2 added to itself 6 times, then the result is multiplied by 3.
Or even:
- 3 added to itself 6 times, then the result is multiplied by 2.
This demonstrates the commutative property of multiplication, meaning the order of the numbers doesn't affect the final product. This flexibility allows us to choose the most efficient method for calculation, based on our understanding of the numbers involved.
Solving 6 x 2 x 3: Different Approaches
Several methods can be used to solve this multiplication problem. Let's explore some:
-
Step-by-Step Calculation: This is the most straightforward approach. We perform the multiplication sequentially:
- 6 x 2 = 12
- 12 x 3 = 36
Therefore, 6 x 2 x 3 = 36
-
Using the Commutative Property: We can rearrange the numbers to simplify the calculation. For example:
- 2 x 3 = 6
- 6 x 6 = 36
This approach leverages the commutative property to make the calculation easier by multiplying smaller numbers first.
-
Mental Math: With practice, one can perform this calculation mentally. Recognizing that 6 x 2 is 12, and then quickly multiplying 12 by 3 to arrive at 36 requires only a basic understanding of multiplication tables.
The Associative Property: Grouping Numbers for Efficiency
The associative property of multiplication states that the grouping of numbers does not change the result. This means that (6 x 2) x 3 is equivalent to 6 x (2 x 3). This property is particularly helpful when dealing with more complex multiplication problems involving numerous factors.
Beyond the Basic Calculation: Applications of Multiplication
The seemingly simple equation "6 x 2 x 3 = 36" has far-reaching applications across numerous fields:
-
Everyday Life: Imagine you're buying 6 packs of juice boxes, each containing 2 rows of 3 juice boxes. The total number of juice boxes is 6 x 2 x 3 = 36. This exemplifies how multiplication is integral to everyday quantity calculations.
-
Geometry: Consider a rectangular prism (a 3D box) with dimensions of 6 units long, 2 units wide, and 3 units high. The volume of this prism is calculated by multiplying its dimensions: 6 x 2 x 3 = 36 cubic units. This demonstrates multiplication's importance in calculating volume and spatial relationships.
-
Physics and Engineering: Multiplication underpins numerous calculations in physics and engineering, ranging from calculating forces and energy to determining the velocity and acceleration of objects. Understanding multiplication is fundamental to grasping the principles of these disciplines.
Exploring Further Mathematical Concepts: Factors and Multiples
The expression "6 x 2 x 3 = 36" introduces several important mathematical concepts:
-
Factors: The numbers 6, 2, and 3 are factors of 36, meaning they divide 36 evenly without leaving a remainder. Identifying factors is crucial in many mathematical operations, such as simplifying fractions and finding the greatest common divisor.
-
Multiples: 36 is a multiple of 6, 2, and 3. Understanding multiples is essential in various mathematical applications, including solving equations and working with fractions.
-
Prime Factorization: The prime factorization of 36 is 2² x 3². This signifies that 36 can be expressed as the product of its prime factors (2 and 3). Prime factorization has significant applications in cryptography and other advanced mathematical fields.
Expanding the Concept: Multiplication with Larger Numbers
While "6 x 2 x 3" is relatively simple, the same principles apply to more complex multiplication problems involving larger numbers. Mastering the fundamental principles of multiplication is crucial for tackling these more challenging calculations. The use of calculators and other computational tools can also aid in solving these more complex problems; however, understanding the underlying principles remains key.
Connecting to Other Mathematical Operations: Division and Fractions
Multiplication and division are inverse operations. Just as 6 x 2 x 3 = 36, we can reverse this calculation through division: 36 / 3 = 12, 12 / 2 = 6. This inverse relationship allows us to solve various types of problems involving multiplication and division.
Fractions are also closely related to multiplication. For example, finding 1/3 of 36 is the same as multiplying 36 by 1/3, which results in 12. Understanding this interconnectedness strengthens our overall mathematical abilities.
Frequently Asked Questions (FAQs)
Q: Is there only one way to solve 6 x 2 x 3?
A: No, due to the commutative and associative properties of multiplication, there are multiple ways to solve this equation. You can change the order of the numbers and group them differently without altering the final answer.
Q: What if we had more than three numbers to multiply?
A: The same principles apply. You would simply continue to multiply the numbers sequentially, or use the commutative and associative properties to simplify the calculation. Calculators are often employed for complex multiplication problems with multiple factors.
Q: How can I improve my multiplication skills?
A: Practice is key. Memorizing multiplication tables, solving practice problems, and using various methods (mental math, written calculations) will improve your speed and accuracy.
Q: Are there any tricks for multiplying larger numbers?
A: Yes, several multiplication tricks and techniques can simplify the process, such as using the distributive property or employing lattice multiplication. These advanced techniques are often taught in higher-level mathematics.
Conclusion: The Importance of Understanding the Fundamentals
The equation "6 x 2 x 3 = 36" might seem trivial at first glance. However, by exploring its underlying principles and applications, we uncover the power and versatility of multiplication. Understanding this seemingly simple operation provides a strong foundation for more advanced mathematical concepts and has practical applications in various aspects of our lives. Mastering multiplication is not merely about arriving at the correct answer; it's about comprehending the logic, appreciating the properties, and recognizing its wide-ranging impact across various fields of study and everyday life. Continued exploration and practice will solidify your understanding and pave the way for further mathematical success.
Latest Posts
Latest Posts
-
Canopy Layer Rainforest
Sep 20, 2025
-
Simplify 20 12
Sep 20, 2025
-
2 5 Of 25000
Sep 20, 2025
-
40l To Gallons
Sep 20, 2025
-
1 4 9
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 6 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.