Simplify 20 12
interactiveleap
Sep 20, 2025 · 6 min read
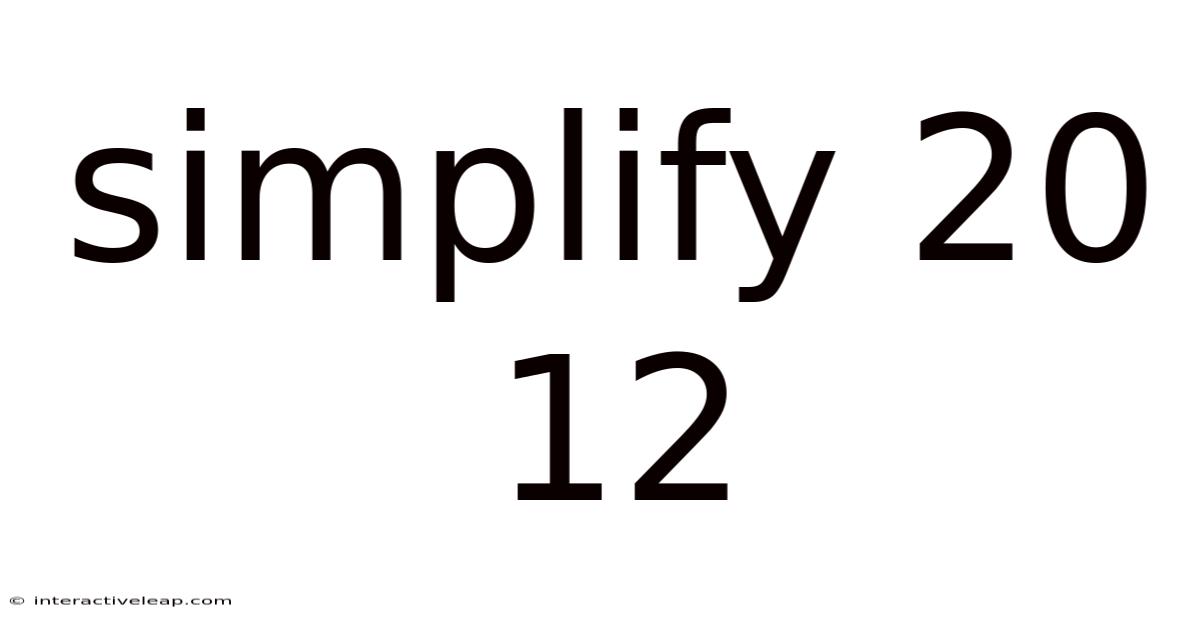
Table of Contents
Simplifying 20/12: A Comprehensive Guide to Fraction Reduction
The seemingly simple task of simplifying fractions can sometimes feel overwhelming, especially when dealing with larger numbers. This comprehensive guide will walk you through the process of simplifying the fraction 20/12, explaining not just the mechanics but also the underlying mathematical principles. We'll cover various methods, delve into the concept of greatest common divisors (GCD), and answer frequently asked questions to ensure a thorough understanding. This guide is designed for students of all levels, from elementary school to high school, and even those looking to refresh their basic math skills. Understanding fraction simplification is a crucial building block for more advanced mathematical concepts.
Understanding Fractions: A Quick Recap
Before we dive into simplifying 20/12, let's quickly recap what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In the fraction 20/12, 20 is the numerator and 12 is the denominator. This means we have 20 parts out of a possible 12 parts. Simplifying a fraction means expressing it in its lowest terms, meaning that the numerator and the denominator share no common factors other than 1.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Once we find the GCD, we divide both the numerator and the denominator by it to obtain the simplified fraction.
Let's find the GCD of 20 and 12. We can use a few methods:
-
Listing Factors: List all the factors of 20 (1, 2, 4, 5, 10, 20) and 12 (1, 2, 3, 4, 6, 12). The largest number that appears in both lists is 4. Therefore, the GCD of 20 and 12 is 4.
-
Prime Factorization: Break down both numbers into their prime factors. The prime factorization of 20 is 2 x 2 x 5 (or 2² x 5). The prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). The common prime factors are 2 x 2 = 4. Therefore, the GCD is 4.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 20 by 12: 20 ÷ 12 = 1 with a remainder of 8.
- Divide 12 by 8: 12 ÷ 8 = 1 with a remainder of 4.
- Divide 8 by 4: 8 ÷ 4 = 2 with a remainder of 0.
The last non-zero remainder is 4, so the GCD is 4.
Now that we know the GCD is 4, we divide both the numerator and denominator of 20/12 by 4:
20 ÷ 4 = 5 12 ÷ 4 = 3
Therefore, the simplified fraction is 5/3.
Method 2: Stepwise Simplification
If you don't immediately see the GCD, you can simplify the fraction step-by-step by dividing both the numerator and denominator by any common factor you can identify. This method might take longer but is helpful if you're not comfortable with finding the GCD directly.
Let's simplify 20/12 step-by-step:
-
Notice that both 20 and 12 are even numbers, meaning they are both divisible by 2. Divide both by 2:
20 ÷ 2 = 10 12 ÷ 2 = 6
The fraction becomes 10/6.
-
Both 10 and 6 are still even, so divide both by 2 again:
10 ÷ 2 = 5 6 ÷ 2 = 3
The fraction becomes 5/3.
Since 5 and 3 have no common factors other than 1, the fraction 5/3 is simplified.
Method 3: Using a Fraction Calculator
While understanding the process is crucial, you can use a fraction calculator to verify your answer. Many online calculators and apps can simplify fractions instantly. However, it's essential to understand the underlying mathematical principles to solve these problems independently.
Improper Fractions and Mixed Numbers
The simplified fraction 5/3 is an improper fraction because the numerator (5) is larger than the denominator (3). We can convert this improper fraction into a mixed number. To do this, we divide the numerator by the denominator:
5 ÷ 3 = 1 with a remainder of 2.
The quotient (1) becomes the whole number part, and the remainder (2) becomes the numerator of the fractional part, keeping the same denominator (3). Therefore, 5/3 is equal to 1 2/3.
Explanation of the Mathematical Principles
The simplification of fractions is based on the fundamental principle of equivalent fractions. Multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction. This is because we are essentially multiplying or dividing by 1 (e.g., 4/4 = 1).
When we simplify a fraction, we are essentially dividing both the numerator and the denominator by their GCD. This ensures that we find the simplest form of the fraction without changing its value.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand and work with. It's crucial for further mathematical operations, especially when dealing with more complex equations and problems.
-
Q: What if I choose a different common factor to start with?
- A: You'll still arrive at the same simplified fraction eventually. It might just take a few more steps.
-
Q: Can I simplify fractions with negative numbers?
- A: Yes, the process remains the same. Consider the absolute values of the numbers when finding the GCD. If the signs are different, the resulting simplified fraction will be negative.
-
Q: What if the GCD is 1?
- A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form.
Conclusion
Simplifying the fraction 20/12 involves finding the greatest common divisor (GCD) of 20 and 12, which is 4. By dividing both the numerator and denominator by 4, we obtain the simplified fraction 5/3, which can also be expressed as the mixed number 1 2/3. Understanding the concept of GCD and the principles of equivalent fractions is crucial for mastering fraction simplification. This skill is foundational for numerous mathematical concepts and applications. By mastering these techniques, you build a solid foundation for future mathematical endeavors. Remember to practice regularly, and don't hesitate to use multiple methods to reinforce your understanding. The more you practice, the more confident you'll become in simplifying fractions of any size.
Latest Posts
Latest Posts
-
510 In Meters
Sep 20, 2025
-
Decimal Of 4 7
Sep 20, 2025
-
6 Divided 0
Sep 20, 2025
-
Curtis House Woodbury
Sep 20, 2025
-
Opposite Of Diligence
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Simplify 20 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.