1 4 9
interactiveleap
Sep 20, 2025 · 5 min read
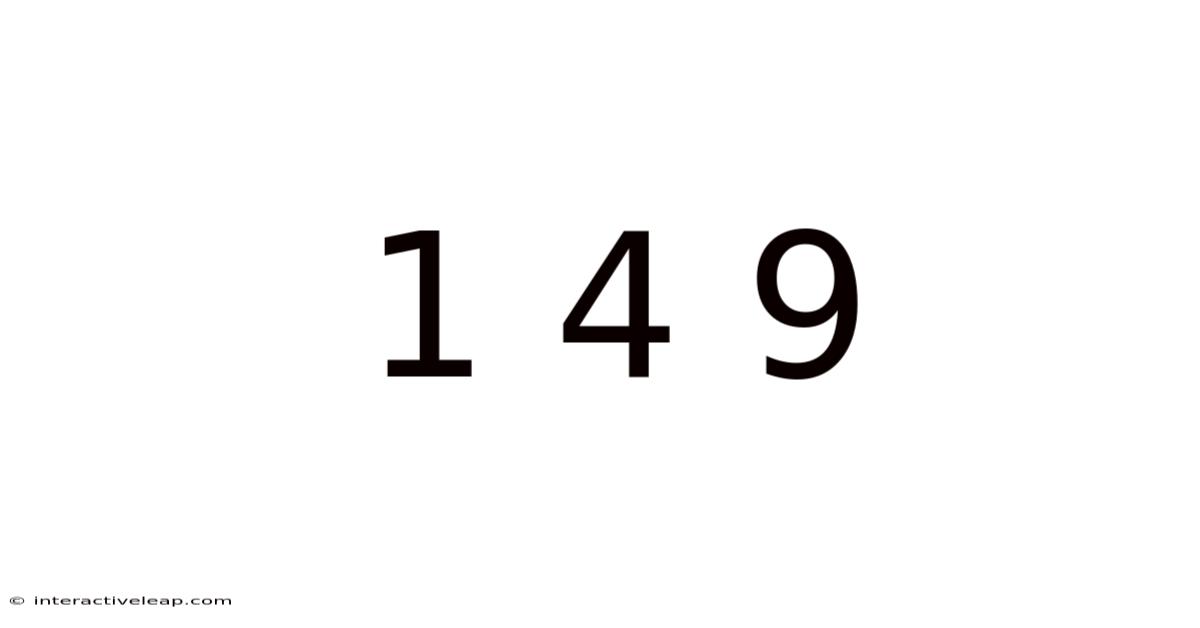
Table of Contents
Unlocking the Secrets of 1, 4, 9: A Journey into Number Patterns, Mathematical Concepts, and their Surprising Applications
The seemingly simple sequence 1, 4, 9… might appear unremarkable at first glance. However, this deceptively straightforward progression holds a wealth of mathematical significance, revealing fascinating patterns and connections that extend far beyond basic arithmetic. This article delves into the world of 1, 4, 9, exploring its foundations in square numbers, its applications in various mathematical fields, and its surprising appearances in seemingly unrelated areas. We will uncover the beauty and power hidden within this fundamental numerical sequence, suitable for readers from a variety of mathematical backgrounds.
Understanding the Foundation: Perfect Squares
The sequence 1, 4, 9… is, in its essence, a sequence of perfect squares. A perfect square is a number that can be obtained by squaring an integer (multiplying an integer by itself). Let's break this down:
- 1 is 1² (1 multiplied by 1)
- 4 is 2² (2 multiplied by 2)
- 9 is 3² (3 multiplied by 3)
Continuing the sequence, we get 16 (4²), 25 (5²), 36 (6²), and so on. This fundamental connection to squares underpins the numerous mathematical properties and applications of this sequence.
Exploring the Pattern: Differences and Relationships
Beyond simply recognizing them as squares, let's analyze the patterns within the sequence itself. Looking at the differences between consecutive terms reveals another intriguing pattern:
- The difference between 4 and 1 is 3.
- The difference between 9 and 4 is 5.
- The difference between 16 and 9 is 7.
Notice a pattern? The differences themselves form an arithmetic sequence: 3, 5, 7… This sequence increases by 2 with each successive term. This observation allows us to predict the next term in the original sequence (1, 4, 9…) by adding the next odd number to the previous term. This simple pattern is surprisingly powerful in understanding and extending the sequence.
The Sequence in Algebra and Geometry
The sequence of perfect squares plays a significant role in various areas of algebra and geometry.
-
Quadratic Equations: The solutions to many quadratic equations (equations of the form ax² + bx + c = 0) often involve square roots, directly connecting them to the sequence 1, 4, 9….
-
Area Calculations: In geometry, the sequence represents the areas of squares with side lengths of 1, 2, 3, and so on. This connection makes the sequence invaluable in calculating areas and volumes in two-dimensional and three-dimensional geometry problems.
-
Pythagorean Theorem: The Pythagorean theorem (a² + b² = c²), a cornerstone of geometry, directly uses squares. Understanding perfect squares helps in applying and understanding this fundamental theorem. Many right-angled triangle problems involve finding the hypotenuse, directly linking to the square numbers sequence.
Applications Beyond Basic Mathematics
The sequence 1, 4, 9… transcends the boundaries of basic arithmetic and geometry, appearing in surprising and unexpected ways across various disciplines:
-
Physics: In physics, particularly in classical mechanics, many equations related to motion, energy, and force involve squared terms, making the sequence relevant to numerous calculations. For example, kinetic energy is calculated as 1/2 * mv², where v² directly links to the sequence.
-
Computer Science: In computer science, algorithms often involve iterations and nested loops, and the computational complexity can be expressed using square functions, again connecting to the sequence 1, 4, 9… The efficiency of certain algorithms is directly related to the square of the input size.
-
Statistics and Probability: In statistics, the concept of variance and standard deviation involves squaring values. The sequence, therefore, finds application in calculating these important statistical measures.
The Sequence and its Visual Representation
The sequence 1, 4, 9… also lends itself beautifully to visual representations. Imagine constructing squares with side lengths 1, 2, 3, and so on. The areas of these squares perfectly represent the numerical sequence. This visual approach aids in grasping the concept intuitively and reinforces the relationship between numbers and geometry. Furthermore, these visual representations can be used to explain concepts like area and volume in a more engaging and approachable way for students.
Frequently Asked Questions (FAQ)
Q: Is there a formula to calculate the nth term in the sequence 1, 4, 9…?
A: Yes, the nth term of the sequence can be calculated using the formula n². For example, the 5th term (n=5) is 5² = 25.
Q: Are there any other interesting patterns within this sequence?
A: Yes, besides the differences between consecutive terms forming an arithmetic progression, the sum of the first n terms also follows a pattern. The sum of the first n perfect squares is given by the formula n(n+1)(2n+1)/6.
Q: How does this sequence relate to other mathematical concepts?
A: The sequence is intimately connected to concepts like quadratic functions, arithmetic progressions, geometric progressions, and even calculus (specifically, summation and integration). It serves as a fundamental building block for many advanced mathematical ideas.
Conclusion: The Enduring Significance of 1, 4, 9…
The seemingly simple sequence 1, 4, 9… reveals a depth and complexity that extends far beyond its initial appearance. From its foundations as perfect squares to its applications in various fields of mathematics, science, and computer science, this sequence demonstrates the interconnectedness of mathematical concepts and their widespread relevance. Understanding this sequence provides a strong foundation for grasping more advanced mathematical ideas, highlighting the beauty and elegance found within even the most basic numerical patterns. Its consistent presence across different disciplines underscores its significance and enduring relevance in the world of mathematics and beyond. The exploration of 1, 4, 9… is not just an exercise in number recognition; it's a journey into the fascinating world of mathematical patterns and their profound implications. This journey encourages us to look beyond the surface of numbers and appreciate the underlying structure and beauty that governs their relationships.
Latest Posts
Latest Posts
-
151lbs In Kg
Sep 20, 2025
-
3000mg In G
Sep 20, 2025
-
A Boat Ore
Sep 20, 2025
-
Sunbed To Buy
Sep 20, 2025
-
Sparx Maths Answer
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 4 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.