40 Of 260
interactiveleap
Sep 15, 2025 · 5 min read
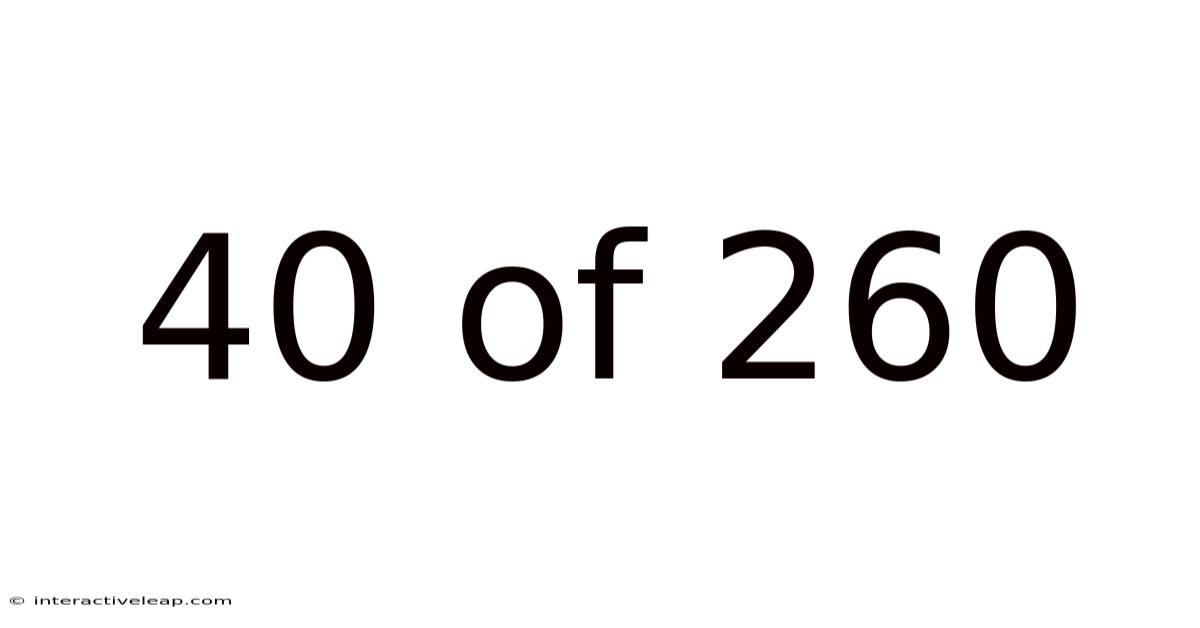
Table of Contents
Decoding 40 of 260: Understanding Fractions and Proportions
The seemingly simple expression "40 of 260" represents a fundamental concept in mathematics: fractions and proportions. Understanding how to interpret and manipulate this type of expression is crucial for a wide range of applications, from everyday tasks like cooking and shopping to more complex scenarios in science, engineering, and finance. This article will delve into the meaning of "40 of 260," explore its different representations, and illustrate its practical applications through various examples. We'll also cover related concepts and answer frequently asked questions to ensure a comprehensive understanding.
What Does "40 of 260" Mean?
At its core, "40 of 260" signifies a part-to-whole relationship. It means 40 represents a portion or fraction of a larger whole, which is 260. In mathematical terms, it can be expressed as a fraction: 40/260. This fraction represents the ratio of 40 to 260. This ratio can be simplified, which we'll explore in the next section.
Simplifying the Fraction: Finding the Simplest Form
The fraction 40/260 can be simplified by finding the greatest common divisor (GCD) of the numerator (40) and the denominator (260). The GCD is the largest number that divides both 40 and 260 without leaving a remainder. In this case, the GCD of 40 and 260 is 20. To simplify the fraction, we divide both the numerator and the denominator by the GCD:
40 ÷ 20 = 2 260 ÷ 20 = 13
Therefore, the simplified fraction is 2/13. This means that 40 is 2/13 of 260. This simplified form is crucial for easier calculations and understanding the proportion.
Representing the Proportion in Different Ways
Besides the fraction form (2/13), "40 of 260" can also be represented in other ways:
-
Decimal: To convert the fraction 2/13 to a decimal, we divide the numerator by the denominator: 2 ÷ 13 ≈ 0.1538. This means 40 represents approximately 15.38% of 260.
-
Percentage: Multiplying the decimal by 100 gives us the percentage: 0.1538 × 100 ≈ 15.38%. So, 40 is approximately 15.38% of 260.
-
Ratio: The ratio of 40 to 260 can be written as 40:260, which simplifies to 2:13. This indicates the proportional relationship between the two numbers.
Practical Applications of Understanding Proportions
Understanding fractions and proportions like "40 of 260" has numerous real-world applications:
-
Calculating Percentages: Imagine a test with 260 total points, and a student scores 40 points. Using the simplified fraction 2/13 or the percentage 15.38%, we can easily determine the student's score as a percentage of the total points.
-
Scaling Recipes: If a recipe calls for 260 grams of flour and you only want to make a smaller portion, understanding the proportion allows you to calculate the amount of flour needed for a smaller batch. For example, if you want to use only 40 grams of flour, you are using 2/13 of the original recipe.
-
Analyzing Data: In statistical analysis, proportions are used extensively to represent parts of a whole. For instance, if a survey of 260 people shows that 40 prefer a particular brand, the fraction 2/13 helps represent the preference proportion.
-
Financial Calculations: Proportions are fundamental in financial calculations, such as determining interest rates, calculating investment returns, and analyzing financial statements.
Solving Problems Involving Proportions
Let's illustrate the application of this knowledge with a few examples:
Example 1: A fruit seller has 260 apples. He sells 40 of them. What percentage of his apples did he sell?
Solution: We already know that 40 out of 260 is equivalent to 2/13. To find the percentage, we convert the fraction to a decimal and multiply by 100: (2/13) * 100 ≈ 15.38%. The fruit seller sold approximately 15.38% of his apples.
Example 2: A school has 260 students. If 2/13 of the students participate in sports, how many students participate in sports?
Solution: We know the fraction (2/13) and the total number of students (260). To find the number of students participating in sports, we multiply the total number of students by the fraction: (2/13) * 260 = 40. Therefore, 40 students participate in sports.
Example 3: A painter needs 260ml of paint to cover a wall. If he only uses 40ml, what fraction of the wall did he cover?
Solution: The fraction of the wall covered is 40/260, which simplifies to 2/13. He covered 2/13 of the wall.
Further Exploration: Ratios and Rates
The concept of "40 of 260" is closely related to ratios and rates. A ratio compares two quantities, while a rate compares two quantities with different units. In our case, the ratio is 40:260 or 2:13. If we were to introduce a time element, for instance, "40 apples sold in 2 hours," we would be dealing with a rate (apples per hour).
Frequently Asked Questions (FAQ)
Q1: Can I simplify 40/260 any further than 2/13?
A1: No, 2/13 is the simplest form because 2 and 13 are prime numbers (numbers divisible only by 1 and themselves) and have no common divisors other than 1.
Q2: What if the numbers were larger? How would I simplify the fraction?
A2: For larger numbers, you can use the Euclidean algorithm to find the GCD. Alternatively, you can find prime factorizations of the numerator and denominator, then cancel out common factors.
Q3: Are there any online tools to simplify fractions?
A3: Yes, many online calculators can simplify fractions automatically. Simply input the numerator and denominator, and the calculator will provide the simplified form.
Q4: How do I convert a fraction to a percentage?
A4: To convert a fraction to a percentage, divide the numerator by the denominator, and then multiply the result by 100%.
Q5: What are some real-world applications beyond the examples given?
A5: Proportions are vital in various fields such as map scaling, mixing solutions (chemistry), calculating probabilities (statistics), and many more.
Conclusion
Understanding "40 of 260" goes beyond simple arithmetic; it’s about grasping the fundamental concepts of fractions, proportions, ratios, and percentages. These concepts are interwoven and essential for problem-solving in numerous contexts. By mastering these fundamental mathematical principles, you'll be better equipped to navigate real-world challenges and analyze data effectively across diverse fields. The ability to simplify fractions, convert between different representations, and apply proportional reasoning is a valuable skill with lasting implications. Remember, the seemingly simple "40 of 260" opens a door to a deeper understanding of the mathematical world around us.
Latest Posts
Latest Posts
-
28 40 Simplified
Sep 15, 2025
-
Luffy Wanted Poster
Sep 15, 2025
-
5 16 Of 286
Sep 15, 2025
-
Minutes To Years
Sep 15, 2025
-
54 8kg To Stone
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 260 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.