5/16 Of 286
interactiveleap
Sep 15, 2025 · 5 min read
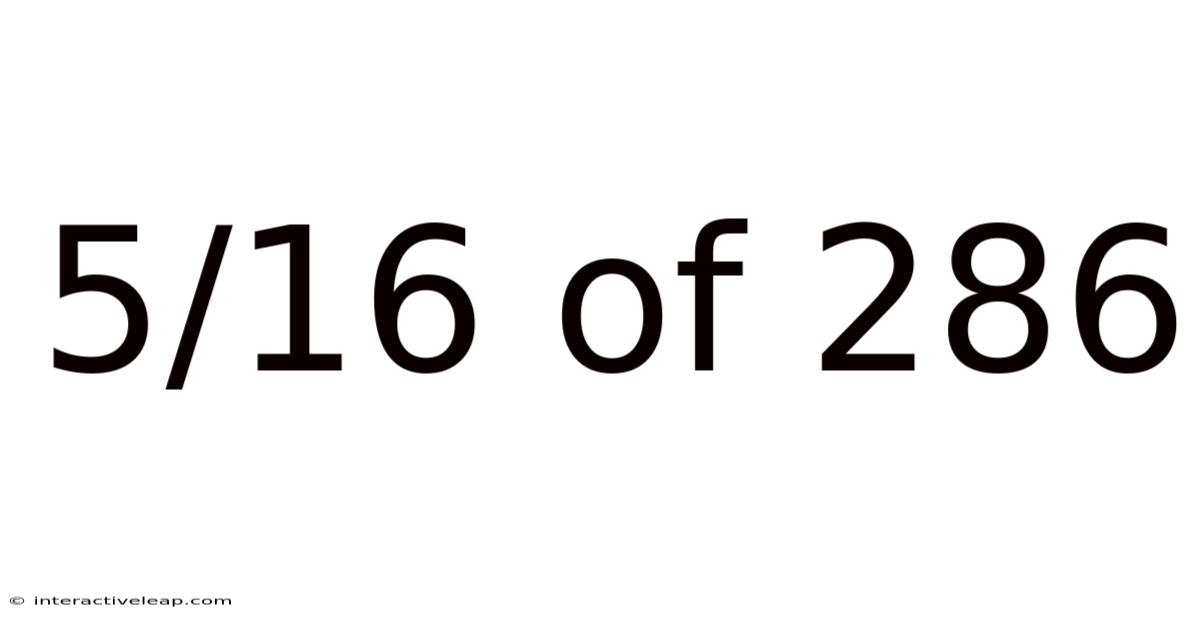
Table of Contents
Decoding 5/16 of 286: A Comprehensive Guide to Fraction Multiplication
Understanding fractions is a cornerstone of mathematics, impacting various aspects of our lives from cooking and construction to finance and programming. This article delves into the seemingly simple problem of calculating 5/16 of 286, but it goes far beyond a mere numerical answer. We'll explore the underlying principles, different solution methods, real-world applications, and common misconceptions surrounding fraction multiplication. By the end, you'll not only know the answer but also grasp the broader concepts involved, equipping you with the confidence to tackle similar problems with ease.
Understanding the Problem: 5/16 of 286
The phrase "5/16 of 286" translates mathematically to the multiplication problem: (5/16) * 286. This means we need to find five-sixteenths of the whole number 286. This seemingly straightforward calculation provides a perfect platform to explore several crucial mathematical concepts.
Method 1: Direct Multiplication
The most straightforward approach involves directly multiplying the fraction by the whole number. This method is best understood by converting the whole number into a fraction with a denominator of 1:
(5/16) * (286/1)
Now, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(5 * 286) / (16 * 1) = 1430 / 16
This leaves us with an improper fraction (where the numerator is larger than the denominator). To simplify, we perform the division:
1430 ÷ 16 = 89.375
Therefore, 5/16 of 286 is 89.375.
Method 2: Simplification Before Multiplication
Often, simplifying fractions before multiplying can make the calculation significantly easier. In this case, we can observe that 286 is an even number, and 16 is also even, implying they share a common factor. Let's find the greatest common divisor (GCD) of 286 and 16.
The prime factorization of 16 is 2⁴. The prime factorization of 286 is 2 x 11 x 13.
The GCD of 16 and 286 is 2. This allows us to simplify:
(5/16) * (286/1) = (5/8) * (143/1) = 715/8
Now, performing the division:
715 ÷ 8 = 89.375
This method demonstrates that simplifying beforehand reduces the size of the numbers involved, making the final division less cumbersome.
Method 3: Converting the Fraction to a Decimal
Another approach is to convert the fraction 5/16 into its decimal equivalent before multiplying. To do this, we perform the division:
5 ÷ 16 = 0.3125
Now, multiply this decimal by 286:
0.3125 * 286 = 89.375
This method offers an alternative perspective, highlighting the interchangeability between fractions and decimals.
Real-World Applications
Understanding fraction multiplication has numerous practical applications:
-
Construction and Engineering: Calculating material quantities, determining proportions in concrete mixes, or scaling blueprints accurately all involve fraction manipulation. Imagine calculating the amount of lumber needed for a project where only a fraction of a standard length is required for a specific component.
-
Cooking and Baking: Recipes frequently call for fractional amounts of ingredients. Scaling a recipe up or down requires multiplying fractional quantities. For instance, if a recipe calls for 1/4 cup of sugar, and you want to double the recipe, you multiply 1/4 by 2.
-
Finance: Calculating interest, discounts, or proportions of investments all require working with fractions or percentages (which are essentially fractions with a denominator of 100). For example, determining the commission on a sale might involve calculating a certain fraction of the total sale value.
-
Data Analysis: Interpreting data and finding percentages or proportions within a dataset frequently involves working with fractions. For instance, finding the proportion of survey respondents who prefer a certain product requires fraction arithmetic.
-
Everyday Life: Many everyday tasks involve using fractions implicitly or explicitly. Sharing items fairly between a group of people, measuring ingredients, or calculating distances often use fractions.
Common Misconceptions about Fraction Multiplication
Several common misconceptions can lead to errors in fraction calculations:
-
Incorrect Order of Operations: Remember that multiplication and division have equal precedence, so you can perform these operations from left to right.
-
Forgetting to Simplify: Failing to simplify the fraction before or after multiplication can lead to larger, more unwieldy numbers and increase the likelihood of calculation errors.
-
Incorrect Conversion to Decimals: When converting fractions to decimals, always ensure the division is carried out accurately. Rounding too early can introduce errors into the final result.
-
Confusion with Addition/Subtraction: Remember that multiplying fractions differs fundamentally from adding or subtracting them. You do not need a common denominator for multiplication.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to solve this?
A: Absolutely! Calculators are valuable tools for verifying your manual calculations, especially for more complex fraction problems. However, understanding the underlying principles is crucial for developing problem-solving skills.
Q: What if the whole number wasn't 286, but a different number?
A: The methods described above apply to any whole number. Simply substitute the new whole number into the equations and follow the same steps.
Q: What if the fraction wasn't 5/16?
A: Again, the principles remain the same. Replace 5/16 with the new fraction, and follow the steps outlined above. The key is understanding the process of fraction multiplication.
Q: Why is simplifying important?
A: Simplifying reduces the size of the numbers you’re working with, making the calculations easier and less prone to errors. It also presents the answer in its simplest form.
Conclusion: Beyond the Numbers
This exploration of calculating 5/16 of 286 has demonstrated that mastering fraction multiplication involves more than just plugging numbers into a formula. It requires a deep understanding of mathematical principles, the ability to choose efficient solution methods, and the awareness of common pitfalls. The real-world applicability of these skills underscores the importance of mastering this fundamental aspect of mathematics. By understanding the different methods and their applications, you'll be better equipped to tackle various mathematical challenges, both in academic settings and in everyday life. Remember, the beauty of mathematics lies not just in the answer, but in the journey of understanding the process.
Latest Posts
Latest Posts
-
Yellow Spot Lizard
Sep 15, 2025
-
54 1kg In Stone
Sep 15, 2025
-
2 X 60
Sep 15, 2025
-
57inches In Cm
Sep 15, 2025
-
Pascal To Mpa
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5/16 Of 286 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.