28 40 Simplified
interactiveleap
Sep 15, 2025 · 6 min read
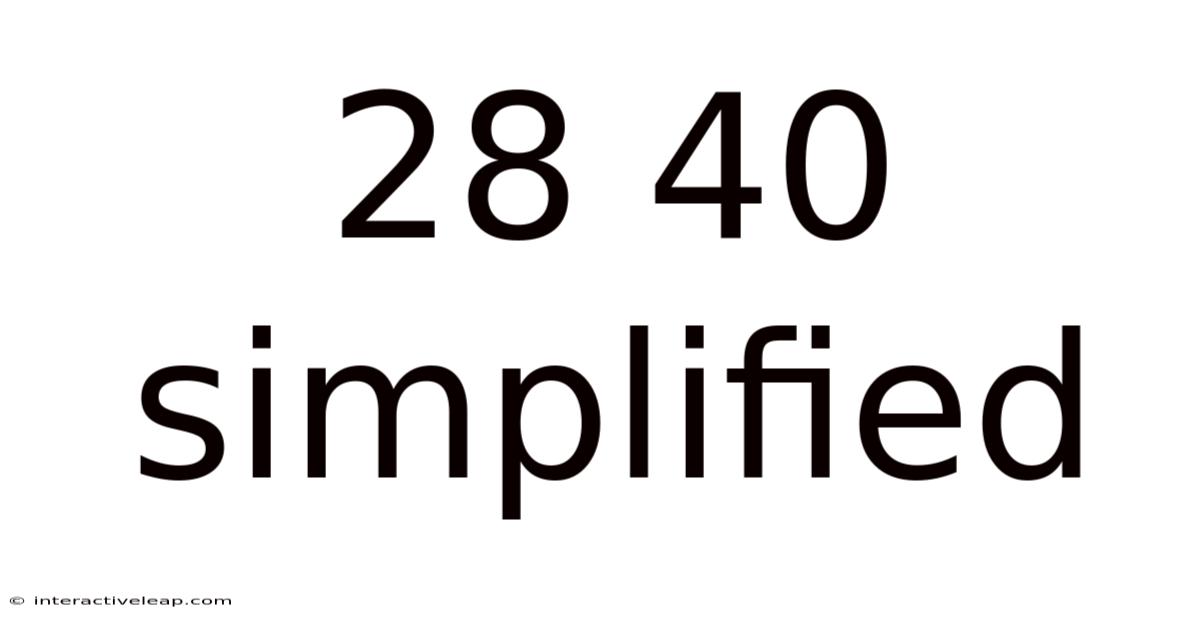
Table of Contents
Decoding 28/40 Simplified: A Comprehensive Guide to Fraction Simplification
Understanding fractions is fundamental to mathematics, and simplifying them is a crucial skill. This guide will thoroughly explain the process of simplifying the fraction 28/40, illustrating the method and delving into the underlying mathematical principles. We'll cover various approaches, including finding the greatest common divisor (GCD), and explore how this skill applies to broader mathematical concepts. By the end, you'll not only know how to simplify 28/40 but also possess a robust understanding of fraction simplification in general.
Understanding Fractions: A Quick Refresher
Before we dive into simplifying 28/40, let's briefly review the components of a fraction. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number (in this case, 28) represents the number of parts we have.
- Denominator: The bottom number (in this case, 40) represents the total number of equal parts the whole is divided into.
Simplifying a fraction means expressing it in its simplest form, where the numerator and denominator have no common factors other than 1. This doesn't change the value of the fraction; it just makes it easier to understand and work with.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD), also known as the greatest common factor (GCF), of the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder.
Let's find the GCD of 28 and 40. We can use several methods:
A. Listing Factors:
- List the factors of 28: 1, 2, 4, 7, 14, 28
- List the factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
- Identify the common factors: 1, 2, 4
- The greatest common factor is 4.
B. Prime Factorization:
This method involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 28: 2 x 2 x 7 (2² x 7)
- Prime factorization of 40: 2 x 2 x 2 x 5 (2³ x 5)
- Identify common prime factors: 2 x 2 = 4
- The greatest common factor is 4.
Once we've found the GCD (which is 4), we divide both the numerator and the denominator by the GCD:
28 ÷ 4 = 7 40 ÷ 4 = 10
Therefore, the simplified fraction is 7/10.
Method 2: Successive Division
This method involves repeatedly dividing the numerator and denominator by common factors until no common factors remain. This method is particularly useful when dealing with larger numbers where finding all factors might be time-consuming.
-
Start with a common factor: Both 28 and 40 are even, so we can divide both by 2: 28 ÷ 2 = 14 40 ÷ 2 = 20
-
Continue dividing: Both 14 and 20 are even, so we divide again by 2: 14 ÷ 2 = 7 20 ÷ 2 = 10
-
Check for further common factors: 7 and 10 have no common factors other than 1.
Therefore, the simplified fraction is 7/10.
Visualizing Fraction Simplification
Imagine you have a pizza cut into 40 slices. You have 28 of those slices (28/40). Simplifying the fraction is like regrouping those slices. Instead of considering individual slices, we group them into sets of 4. You have 7 sets of 4 slices out of a total of 10 sets of 4 slices (7/10). The pizza is the same size; you just have a more manageable way to describe the portion you have.
The Importance of Simplifying Fractions
Simplifying fractions is more than just a mathematical procedure; it's crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret. 7/10 is more intuitive than 28/40.
- Efficiency: Simplified fractions make calculations simpler and faster. Working with 7/10 is significantly easier than working with 28/40, particularly in more complex calculations involving addition, subtraction, multiplication, or division of fractions.
- Comparison: Comparing simplified fractions is much easier. It’s easy to see that 7/10 is greater than 1/2, but comparing 28/40 to 1/2 is less straightforward.
- Accuracy: Simplifying fractions reduces the risk of errors in calculations, especially when dealing with larger numbers.
Applications of Fraction Simplification
The skill of simplifying fractions extends beyond basic arithmetic. It's a fundamental concept used in:
- Algebra: Simplifying algebraic fractions involves similar principles.
- Geometry: Calculations involving ratios and proportions often involve simplifying fractions.
- Calculus: Many calculus operations rely on simplifying complex rational expressions, which are essentially fractions.
- Real-World Applications: Fractions are used in various real-world scenarios, such as cooking (measuring ingredients), construction (measuring materials), and finance (calculating percentages).
Frequently Asked Questions (FAQ)
Q: What if I don't find the GCD immediately?
A: Don't worry! You can use successive division; keep dividing by common factors until you reach the simplest form. It might take a few steps, but you'll eventually get to the simplified fraction.
Q: Is there a shortcut to find the GCD?
A: While listing factors or prime factorization are reliable, using the Euclidean algorithm is a more efficient method for finding the GCD of larger numbers. However, for smaller numbers like 28 and 40, the methods described above are sufficient.
Q: Why is simplifying fractions important in algebra?
A: Simplifying fractions in algebra helps to simplify algebraic expressions, making them easier to manipulate and solve equations. Just like in arithmetic, simplified algebraic fractions lead to clearer and more efficient calculations.
Q: Can I simplify a fraction by only dividing the numerator or denominator?
A: No, you must divide both the numerator and the denominator by the same number to maintain the value of the fraction. Dividing only one part changes the value of the fraction.
Q: Are there any online tools to help with simplifying fractions?
A: While many online calculators exist for simplifying fractions, understanding the underlying process is crucial for applying the concept in various mathematical contexts.
Conclusion
Simplifying the fraction 28/40 to 7/10 is a straightforward process that demonstrates a core concept in mathematics. Mastering this skill not only enhances your arithmetic abilities but also lays the foundation for more advanced mathematical concepts. By understanding the methods of finding the GCD and applying successive division, you can confidently simplify any fraction, making your mathematical journey smoother and more efficient. Remember, the key is to understand the underlying principle: dividing both the numerator and the denominator by their greatest common divisor. This ensures that you are not altering the fundamental value of the fraction while expressing it in the most concise and understandable form.
Latest Posts
Latest Posts
-
Yellow Spot Lizard
Sep 15, 2025
-
54 1kg In Stone
Sep 15, 2025
-
2 X 60
Sep 15, 2025
-
57inches In Cm
Sep 15, 2025
-
Pascal To Mpa
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 28 40 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.