30 Of 65
interactiveleap
Sep 16, 2025 · 5 min read
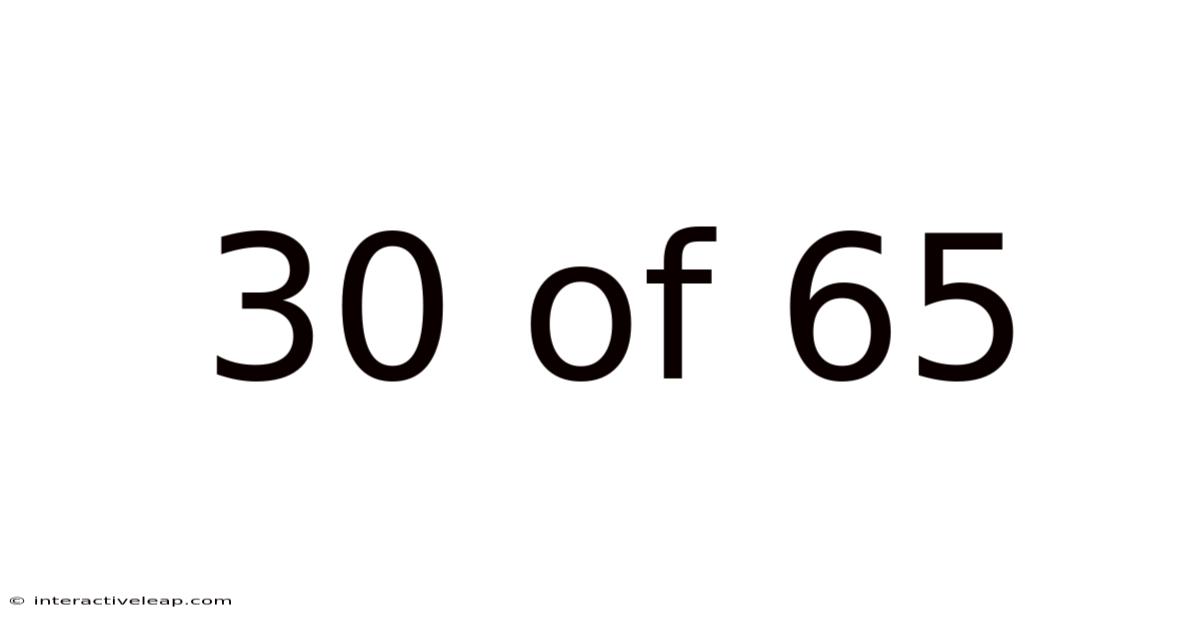
Table of Contents
Decoding the Fraction 30/65: A Deep Dive into Simplification, Applications, and Related Concepts
Understanding fractions is a cornerstone of mathematical literacy, crucial for navigating various aspects of life, from baking a cake to calculating financial proportions. This article delves into the specific fraction 30/65, exploring its simplification, practical applications, and related mathematical concepts. We'll move beyond simple reduction, examining how this fraction fits within the broader landscape of numbers and problem-solving.
Introduction: What is 30/65?
The fraction 30/65 represents 30 parts out of a total of 65 equal parts. This is a common type of fraction, where the numerator (30) is smaller than the denominator (65), indicating a proper fraction – a value less than one. However, this fraction can be simplified, making it easier to work with and understand its true value. This simplification process, crucial for many mathematical operations, forms the foundation of our exploration.
Step-by-Step Simplification of 30/65:
The key to simplifying fractions lies in finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. Let's find the GCD of 30 and 65:
- List the factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- List the factors of 65: 1, 5, 13, 65
- Identify the common factors: 1 and 5
- The greatest common factor (GCF) is 5.
Now, we divide both the numerator and the denominator by the GCD (5):
30 ÷ 5 = 6 65 ÷ 5 = 13
Therefore, the simplified form of 30/65 is 6/13. This simplified fraction represents the same value as 30/65 but is more concise and easier to use in calculations.
Understanding the Concept of Equivalent Fractions:
It's important to understand that 30/65 and 6/13 are equivalent fractions. They represent the same proportion or ratio. This means they occupy the same point on the number line. You can generate numerous equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number. For instance, multiplying 6/13 by 2/2 gives you 12/26, another equivalent fraction.
Practical Applications of 30/65 (and its simplified form 6/13):
Fractions are ubiquitous in daily life. The fraction 30/65, or its simplified equivalent 6/13, could represent various scenarios:
- Proportion of correct answers: If a student answered 30 questions correctly out of a total of 65 questions, their score is 30/65, or simplified, 6/13.
- Part of a whole: Imagine a pizza cut into 65 slices. If 30 slices have been eaten, the remaining portion is 35/65 (which simplifies to 7/13), while the eaten portion is 30/65 (or 6/13).
- Ratio of ingredients: A recipe might call for a ratio of 30 grams of ingredient A to 65 grams of ingredient B, which simplifies to a 6:13 ratio.
- Probability: In a game of chance with 65 equally likely outcomes, if 30 outcomes lead to a specific event, the probability of that event occurring is 30/65, or 6/13.
Converting Fractions to Decimals and Percentages:
To further understand the value of 30/65 (or 6/13), we can convert it to a decimal and a percentage:
- Decimal: Divide the numerator (6) by the denominator (13): 6 ÷ 13 ≈ 0.4615
- Percentage: Multiply the decimal by 100: 0.4615 × 100 ≈ 46.15%
This means 30/65 represents approximately 46.15% of the whole.
Further Exploration: Prime Factorization and Least Common Multiple (LCM)
The simplification process we used earlier implicitly touched upon prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 30: 2 x 3 x 5
- Prime factorization of 65: 5 x 13
Notice that the common factor, 5, is clearly visible in both factorizations. Understanding prime factorization helps in efficiently finding the GCD and the least common multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. This concept is crucial in operations involving fractions with different denominators (finding a common denominator for addition and subtraction).
Frequently Asked Questions (FAQ):
-
Q: Can I simplify 30/65 any further than 6/13?
- A: No, 6 and 13 are both prime numbers, meaning they have no common factors other than 1. Therefore, 6/13 is the simplest form.
-
Q: What if I had simplified 30/65 by dividing by 2 first, obtaining 15/32.5?
- A: This is incorrect because you cannot divide only the numerator and leave the denominator as a decimal. You must divide both the numerator and the denominator by the same whole number.
-
Q: How do I know if I've simplified a fraction completely?
- A: Check if the numerator and the denominator share any common factors other than 1. If they don't, the fraction is in its simplest form. Alternatively, check if both the numerator and the denominator are prime numbers.
Conclusion: The Significance of 30/65 and Fraction Mastery
The seemingly simple fraction 30/65 provides a rich learning opportunity. Beyond its straightforward simplification to 6/13, it highlights fundamental concepts such as equivalent fractions, GCD, prime factorization, and the practical applications of fractions in everyday life. Mastering these concepts is not merely about acing math tests; it equips you with essential analytical and problem-solving skills applicable across various disciplines and real-world situations. Understanding fractions, like understanding 30/65, is a crucial step towards developing a strong foundation in mathematics and its applications. Remember to practice regularly, explore different approaches to simplification, and never hesitate to ask questions. The journey towards mathematical fluency is an ongoing process of learning and discovery.
Latest Posts
Latest Posts
-
Wishes Were Horses
Sep 16, 2025
-
21 Of 230
Sep 16, 2025
-
87 9kg In Stone
Sep 16, 2025
-
4000 60
Sep 16, 2025
-
5000 X 50
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 30 Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.