27 X Pi
interactiveleap
Sep 21, 2025 · 6 min read
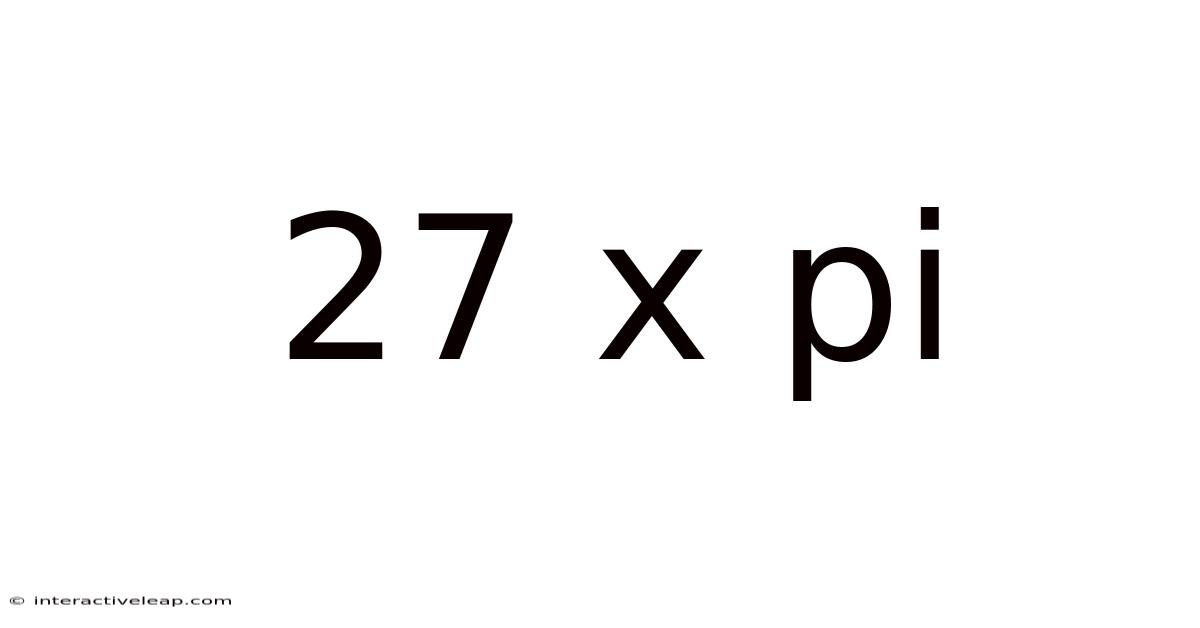
Table of Contents
Unveiling the Mysteries of 27π: A Deep Dive into the Number
The seemingly simple expression "27π" hides a surprising depth of mathematical intrigue. While it might initially appear as just a multiplication of two numbers – 27 and pi (π, approximately 3.14159) – exploring its implications reveals connections to geometry, calculus, physics, and even the fascinating world of approximations and numerical methods. This article delves into the multifaceted nature of 27π, examining its practical applications, theoretical significance, and the broader mathematical context within which it exists. We'll uncover its secrets, moving beyond a simple calculation to a deeper understanding of its inherent properties and significance.
Understanding the Components: 27 and π
Before embarking on a journey into the world of 27π, it's crucial to understand its constituent parts: 27 and π.
-
27: A seemingly unremarkable integer, 27 is a composite number, divisible by 1, 3, 9, and 27. It's also a perfect cube (3³), a fact that holds subtle importance in certain mathematical contexts. Its divisibility by 3 makes it relevant in modular arithmetic and number theory.
-
π (Pi): This is where things get more interesting. Pi is a mathematical constant representing the ratio of a circle's circumference to its diameter. It's an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. The approximation 3.14159 is commonly used, but its true value stretches infinitely, a fact that has fascinated mathematicians for millennia. Pi's appearance in so many areas of mathematics and physics highlights its fundamental importance.
Calculating 27π: Beyond the Obvious
Calculating 27π is straightforward using a calculator or computer software. The result, to several decimal places, is approximately 84.8230016469. However, the simplicity of the calculation belies the deeper implications. The value itself, approximately 84.82, doesn't inherently hold special mathematical significance as a number itself. The significance lies in its derivation and its potential applications within various mathematical and scientific problems.
Applications and Interpretations of 27π
The appearance of 27π in various contexts depends entirely on the specific problem. Let's explore some hypothetical scenarios:
-
Geometry: Imagine a circle with a radius of 27 units. The circumference of this circle would be 27π units. This simple example highlights the direct application of 27π in calculating the perimeter of a circle. Similarly, the area of a circle with a radius of 27/2 would involve 27π as part of the area calculation (Area = πr²).
-
Calculus: In integral calculus, 27π could arise as the result of an integration problem involving trigonometric functions or expressions related to circles. For instance, the integral of a function that describes the area under a curve related to circular shapes may result in 27π. Solving integrals often yields values expressed in terms of π. The specific function dictates whether 27π would arise as a result.
-
Physics: In physics, π frequently appears in formulas related to waves, oscillations, and circular motion. 27π might appear in equations describing the angular displacement of an object rotating at a certain rate, or the amplitude of a wave. The exact physical scenario determines the role of 27π, but its presence would indicate a relationship involving circular or periodic motion.
-
Approximations and Numerical Methods: The irrationality of π presents challenges in practical computations. Numerical methods, such as Taylor series expansions or Monte Carlo simulations, can be used to approximate π to a desired level of accuracy. These methods might involve calculating 27 multiplied by a progressively more precise approximation of π, highlighting the importance of accurate approximation techniques.
Exploring Related Mathematical Concepts
Understanding 27π necessitates exploring related mathematical concepts:
-
Irrational Numbers: The presence of π underscores the importance of irrational numbers in mathematics and the sciences. Their infinite, non-repeating decimal expansions require sophisticated methods for approximation and manipulation in calculations.
-
Circular Functions: Trigonometric functions (sine, cosine, tangent) are intrinsically linked to circles and angles, leading to frequent appearances of π in their calculations and identities. The relationship between these functions and π is fundamental to many areas of mathematics and physics.
-
Series Representations of Pi: Several infinite series converge to π, providing alternative ways to approximate its value. These series are powerful tools in numerical analysis and provide insights into the nature of π itself. These series could potentially involve coefficients that, when multiplied by the limit of the series (π), lead to expressions like 27π.
-
Modular Arithmetic: While not directly related to 27π in an obvious manner, 27's divisibility by 3 allows exploration within the framework of modular arithmetic. This area of mathematics examines remainders when integers are divided, and the properties of 27 in this context might be significant in certain advanced number-theoretical studies.
Frequently Asked Questions (FAQs)
Q: Is 27π a rational or irrational number?
A: 27π is an irrational number. Since π is irrational, any non-zero rational multiple of π (like 27π) will also be irrational. The product of a rational number and an irrational number is always irrational.
Q: What are some practical applications of calculating 27π?
A: Practical applications depend on the context. In engineering, it might be used in calculations involving circular structures or rotating machinery. In computer graphics, it could appear in algorithms related to drawing circles or ellipses. The specifics depend on the situation where the calculation is needed.
Q: How accurate does the approximation of 27π need to be for different applications?
A: The required accuracy of 27π's approximation depends entirely on the application's sensitivity to error. In some scenarios, a rough approximation might suffice, while in others (e.g., precise engineering calculations), a high degree of accuracy is critical.
Q: Are there any special mathematical properties associated with the number 27π?
A: The number 27π itself doesn't possess uniquely special mathematical properties beyond its definition as the product of 27 and π. However, the mathematical concepts surrounding its components (27 and π) are rich with profound implications in various branches of mathematics.
Conclusion: Beyond the Calculation
While the calculation of 27π is simple, its significance extends far beyond a single numerical result. It serves as a gateway to understanding deeper mathematical concepts, such as irrational numbers, circular functions, and the profound importance of π in various fields. Its appearance in different mathematical and scientific contexts highlights the interconnectedness of various branches of knowledge and the pervasive influence of fundamental mathematical constants. Understanding 27π, therefore, is not just about calculating a number; it's about appreciating the rich mathematical tapestry it represents. The seemingly simple expression opens doors to a world of complex and fascinating mathematical ideas, highlighting the beauty and elegance of mathematical principles. Further exploration into these related concepts will undoubtedly reveal even more about the profound significance of this seemingly simple numerical expression.
Latest Posts
Latest Posts
-
The Fire Engine
Sep 21, 2025
-
Enter Your Answer
Sep 21, 2025
-
60 Of 220
Sep 21, 2025
-
2 6 Cos 12
Sep 21, 2025
-
168cm To Inches
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 27 X Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.