2.6 Cos 12
interactiveleap
Sep 21, 2025 · 6 min read
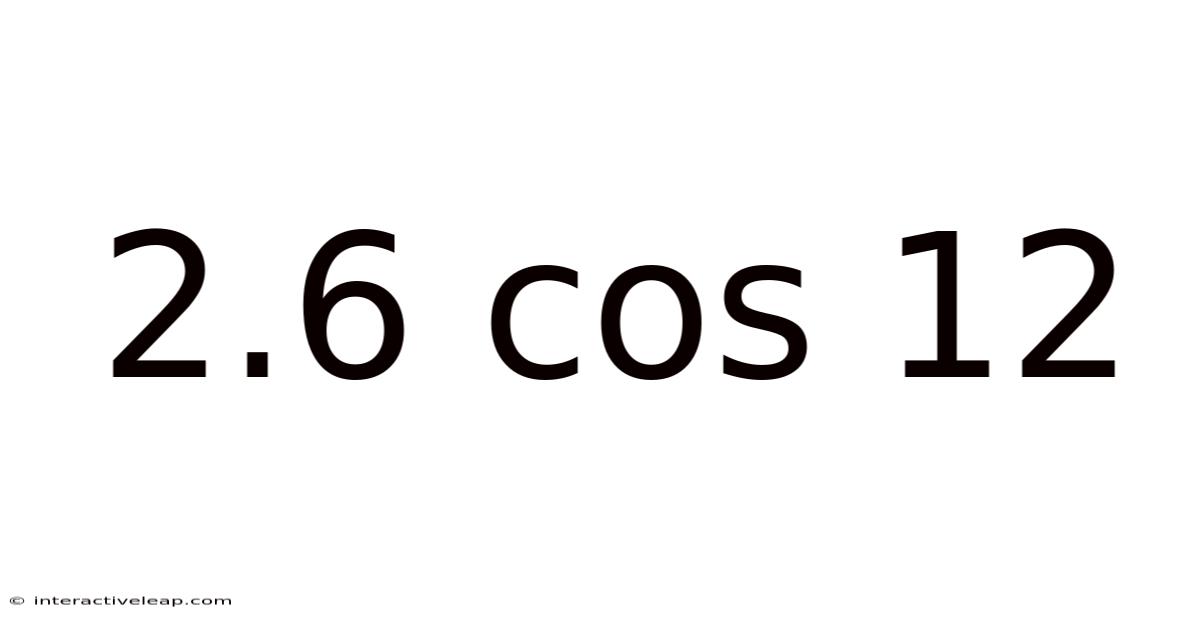
Table of Contents
Decoding 2.6 cos 12: A Deep Dive into Trigonometry and its Applications
This article delves into the meaning and calculation of "2.6 cos 12," exploring the fundamental trigonometric concepts involved and demonstrating its practical applications across various fields. We'll unpack the expression, explaining the significance of each component and outlining the steps involved in its computation. Understanding this seemingly simple expression provides a solid foundation for more complex trigonometric problems and their real-world relevance.
Introduction: Understanding the Components
The expression "2.6 cos 12" combines a constant (2.6), a trigonometric function (cosine), and an angle (12). Let's break down each element:
-
2.6: This is a scalar value, a constant multiplier that scales the result of the cosine function. It could represent a physical quantity like amplitude, distance, or force, depending on the context of the problem.
-
cos: This is the cosine function, one of the fundamental trigonometric functions. It relates the ratio of the adjacent side to the hypotenuse in a right-angled triangle to the angle. In the context of a unit circle, it represents the x-coordinate of a point on the circle. It's crucial to remember that the cosine function operates on angles.
-
12: This is the angle measured in degrees (unless specified otherwise). It's the input to the cosine function. The value of the cosine function changes as the angle changes. The angle could represent various physical phenomena like an angle of elevation, an angle of rotation, or a phase difference in a wave.
Understanding these individual components is essential to interpreting the entire expression and its resulting value. The calculation involves finding the cosine of 12 degrees and then multiplying the result by 2.6.
Calculating 2.6 cos 12: Step-by-Step Guide
Calculating this expression requires a scientific calculator or a trigonometric table. Here's how to do it:
-
Set your calculator to degree mode: Ensure your calculator is set to operate in degrees, not radians. This is critical because the cosine function's output drastically changes based on whether the input is in degrees or radians.
-
Find the cosine of 12 degrees: Enter "cos 12" into your calculator. The result should be approximately 0.9781476.
-
Multiply by 2.6: Multiply the result from step 2 by 2.6. This gives us approximately 2.547184.
Therefore, 2.6 cos 12 ≈ 2.547. The precise value will depend on the precision of your calculator.
The Significance of Cosine in Trigonometry
The cosine function is a cornerstone of trigonometry, playing a vital role in various applications. Its definition within a right-angled triangle forms the basis of its utility.
-
Right-angled Triangle Relationships: In a right-angled triangle, the cosine of an acute angle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. This relationship allows us to determine unknown side lengths or angles given sufficient information.
-
Unit Circle Representation: The cosine function can also be represented using the unit circle. Imagine a circle with a radius of 1. For any angle θ, the x-coordinate of the point where the terminal side of the angle intersects the circle is equal to cos θ.
-
Periodic Nature: Cosine is a periodic function, meaning its values repeat over a specific interval. The period of the cosine function is 360 degrees (or 2π radians). This periodicity is crucial in modeling cyclical phenomena.
Real-World Applications of 2.6 cos 12 and Similar Expressions
While "2.6 cos 12" might seem abstract, expressions like it have numerous real-world applications across various disciplines:
-
Physics: In physics, trigonometric functions are vital in analyzing projectile motion. For example, the horizontal displacement of a projectile can be modeled using a cosine function. The constant 2.6 might represent the initial velocity, and the angle 12 degrees could represent the launch angle. The result would represent the horizontal component of the displacement at a specific time.
-
Engineering: Civil engineers use trigonometry to calculate forces and stresses in structures. For instance, in analyzing a truss bridge, the angle and magnitude of forces acting on different members can be calculated using trigonometric functions. The expression could represent a component of force acting on a particular member.
-
Electronics and Signal Processing: Trigonometric functions, especially cosine, are foundational in signal processing. Cosine waves are used to represent signals, and analysis involves manipulating these signals using trigonometric identities and calculations. The expression could represent the amplitude of a cosine wave at a specific point in time.
-
Computer Graphics: In computer graphics and game development, trigonometric functions are used extensively for rotation, transformations, and perspective calculations. The expression might represent a component of a vector used in a 3D transformation.
-
Navigation and Surveying: Trigonometry is used in navigation and surveying to determine distances, angles, and locations. For instance, a surveyor might use angle measurements and trigonometric functions to calculate the distance between two points.
Understanding Radians: An Alternative Perspective
While the calculation above utilized degrees, angles can also be measured in radians. Radians are a unit of angular measure defined as the ratio of the arc length to the radius of a circle. One radian is the angle subtended at the center of a circle by an arc equal in length to the radius.
To calculate "2.6 cos 12" using radians, we must first convert 12 degrees to radians. The conversion formula is:
Radians = Degrees * (π/180)
Therefore, 12 degrees is equal to (12 * π/180) ≈ 0.2094 radians. Using this radian measure in the cosine function would yield a slightly different (but still related) result. It's crucial to ensure consistency in units when using trigonometric functions.
Frequently Asked Questions (FAQ)
Q: What if the angle was given in radians?
A: If the angle were given in radians, you would directly input the radian value into the cosine function on your calculator, ensuring it is set to radian mode. You would then multiply the result by 2.6.
Q: Can this expression be used with other trigonometric functions like sine or tangent?
A: Yes, absolutely. The same principles apply. You would replace "cos" with "sin" or "tan" and use the appropriate trigonometric function based on the problem's context.
Q: What is the importance of the constant 2.6?
A: The constant 2.6 acts as a scaling factor. Its value will depend entirely on the specific problem being solved. It could represent an amplitude, a magnitude, or any other relevant physical quantity.
Conclusion: Beyond the Numbers
The seemingly simple expression "2.6 cos 12" unveils a wealth of underlying trigonometric concepts and their far-reaching applications. By understanding the individual components and the steps involved in its calculation, we can appreciate the fundamental role of trigonometry in various scientific and engineering disciplines. From projectile motion to signal processing, the principles illustrated here provide a strong foundation for tackling more complex problems and for appreciating the mathematical beauty behind seemingly simple expressions. This deep dive has aimed to not only provide the solution but also to illuminate the context and significance of trigonometric functions in the world around us. Remember that consistent practice and understanding of the underlying concepts are crucial to mastering trigonometry.
Latest Posts
Latest Posts
-
1 73m In Inches
Sep 21, 2025
-
15 Of 80000
Sep 21, 2025
-
118pounds In Kg
Sep 21, 2025
-
1 5 X 7
Sep 21, 2025
-
Long Division Question
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2.6 Cos 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.