250 X 4
interactiveleap
Sep 16, 2025 · 6 min read
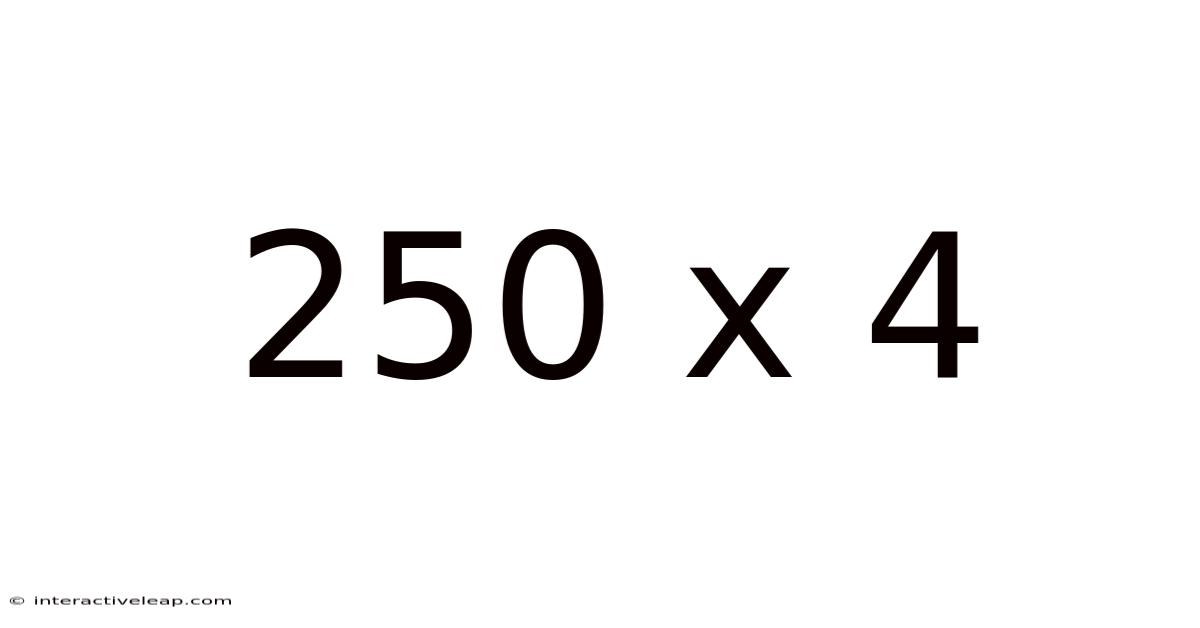
Table of Contents
Decoding 250 x 4: A Deep Dive into Multiplication, Area, and Beyond
This article explores the seemingly simple mathematical expression "250 x 4," delving far beyond the basic arithmetic calculation. We'll examine its practical applications in various fields, uncover the underlying mathematical principles, and even explore its relevance in different contexts – from simple area calculations to more complex real-world scenarios. Understanding this seemingly straightforward problem unlocks a deeper appreciation for the power and versatility of mathematics.
I. The Fundamental Calculation: 250 x 4
At its core, 250 x 4 represents a multiplication problem. In elementary terms, it asks: "What is the total when you add 250 four times?" The answer, easily obtained through basic arithmetic or a calculator, is 1000. However, this simple calculation forms the foundation for understanding more complex concepts.
II. Visualizing Multiplication: Area and Geometry
Imagine a rectangular area. If one side measures 250 units (e.g., centimeters, meters, inches) and the adjacent side measures 4 units, the total area of the rectangle is found by multiplying these two dimensions: 250 x 4 = 1000 square units. This visual representation connects the abstract concept of multiplication to a tangible geometric reality. This understanding is crucial in fields like architecture, engineering, and even everyday tasks like calculating the area of a room to determine the amount of paint or flooring needed.
III. Applications in Real-World Scenarios
The simple calculation of 250 x 4 has numerous real-world applications. Here are a few examples:
-
Business and Finance: Imagine a company selling a product for $250 per unit. If they sell 4 units, their total revenue is 250 x 4 = $1000. This fundamental calculation is the cornerstone of sales and revenue projections.
-
Science and Engineering: In scientific experiments, you might need to repeat a process 4 times, each taking 250 seconds. The total time spent on the experiment would be 250 x 4 = 1000 seconds. This precise calculation ensures accuracy and reliability in scientific studies.
-
Everyday Life: Think about baking. A recipe might call for 250 grams of flour for one batch of cookies. If you want to bake 4 batches, you’ll need 250 x 4 = 1000 grams of flour. This simple multiplication ensures you have the correct ingredients for your baking project.
IV. Breaking Down the Calculation: Distributive Property and Mental Math
Understanding the underlying mathematical principles allows for more efficient calculation. The distributive property allows us to break down the problem into smaller, more manageable parts. For instance:
250 x 4 = (200 + 50) x 4 = (200 x 4) + (50 x 4) = 800 + 200 = 1000
This approach allows for mental calculation without relying solely on a calculator. This technique is particularly useful for improving mental arithmetic skills and for quick estimations.
V. Exploring Different Number Bases:
While we typically work in base 10 (decimal system), we can explore the same calculation in different number bases. For instance, converting 250 and 4 to base 2 (binary), we get:
- 250 (base 10) = 11111010 (base 2)
- 4 (base 10) = 100 (base 2)
Multiplying these binary numbers requires a different approach, involving binary addition and carrying operations. The result, when converted back to base 10, would still be 1000. This demonstrates the universality of the mathematical operation regardless of the number system used.
VI. Advanced Applications: Scaling and Proportionality
The concept of scaling is closely related to multiplication. If we increase the dimensions of a geometric shape by a factor of 4, the area increases by a factor of 4². This illustrates the importance of understanding how changes in one dimension affect others in a proportional manner.
Consider a scenario where a farmer has a field with an area of 250 square meters. If they want to expand their field to four times its current size, they would need 250 x 4 = 1000 square meters of land. This highlights the practical application of multiplication in determining scale and proportional changes.
VII. Error Analysis and Significance
In scientific and engineering contexts, the accuracy of calculations is paramount. Understanding error propagation is crucial. If the initial measurement of 250 has an associated uncertainty, this uncertainty will propagate through the multiplication process, affecting the final result. For instance, if 250 has an uncertainty of ±5, the final result (1000) would also have a corresponding uncertainty. A thorough understanding of significant figures is crucial in ensuring accurate and meaningful results.
VIII. Beyond Arithmetic: Algebraic Representation
The expression "250 x 4" can also be represented algebraically. Let's say 'x' represents the number 250 and 'y' represents the number 4. The expression then becomes x * y = 1000. This algebraic representation allows for more generalized mathematical manipulations and problem-solving.
IX. Connecting to Other Mathematical Concepts
The simple equation 250 x 4 connects to various other mathematical concepts:
- Factors and Multiples: 4 is a factor of 1000, and 1000 is a multiple of 4 and 250.
- Prime Factorization: Understanding the prime factorization of 250 (2 x 5³) and 4 (2²) helps in grasping the factors involved in the multiplication.
- Exponents: The calculation can be expressed as 250 x 4¹ or even as 250 x 2².
X. The Power of Estimation:
In many real-world situations, precise calculation isn't always necessary. Estimation is a valuable skill that allows for quick approximations. Rounding 250 to 250 and 4 to 4 provides an exact answer, but rounding to nearby numbers (e.g., 200 x 4 = 800) can provide a useful estimate for quick decision-making.
XI. Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes made when calculating 250 x 4?
- A: Common mistakes include errors in carrying over digits during manual calculation or misplacing the decimal point when using a calculator. Careful attention to detail minimizes these errors.
-
Q: How can I improve my multiplication skills?
- A: Practice is key. Regularly work through multiplication problems, utilize different calculation methods, and try mental math exercises to build fluency and speed.
-
Q: Are there alternative ways to calculate 250 x 4 besides standard multiplication?
- A: Yes, as discussed, the distributive property, repeated addition, and even binary multiplication are alternative methods.
-
Q: How does understanding 250 x 4 help in more advanced mathematics?
- A: This fundamental understanding forms the basis for more complex concepts like algebra, calculus, and linear algebra, where multiplication is a core operation.
XII. Conclusion:
The seemingly simple calculation of 250 x 4 opens a gateway to a deeper understanding of fundamental mathematical principles, their real-world applications, and their connection to more advanced mathematical concepts. By exploring its various facets, from basic arithmetic to more complex applications, we gain a valuable appreciation for the power and versatility of mathematics in everyday life and beyond. Mastering this simple equation is a stepping stone towards a more profound understanding of the mathematical world.
Latest Posts
Latest Posts
-
32cm To Inch
Sep 16, 2025
-
3 8kg In Lbs
Sep 16, 2025
-
69kg To Stone
Sep 16, 2025
-
35 Of 75
Sep 16, 2025
-
400 X 7
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 250 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.