25 Of 225
interactiveleap
Sep 20, 2025 · 5 min read
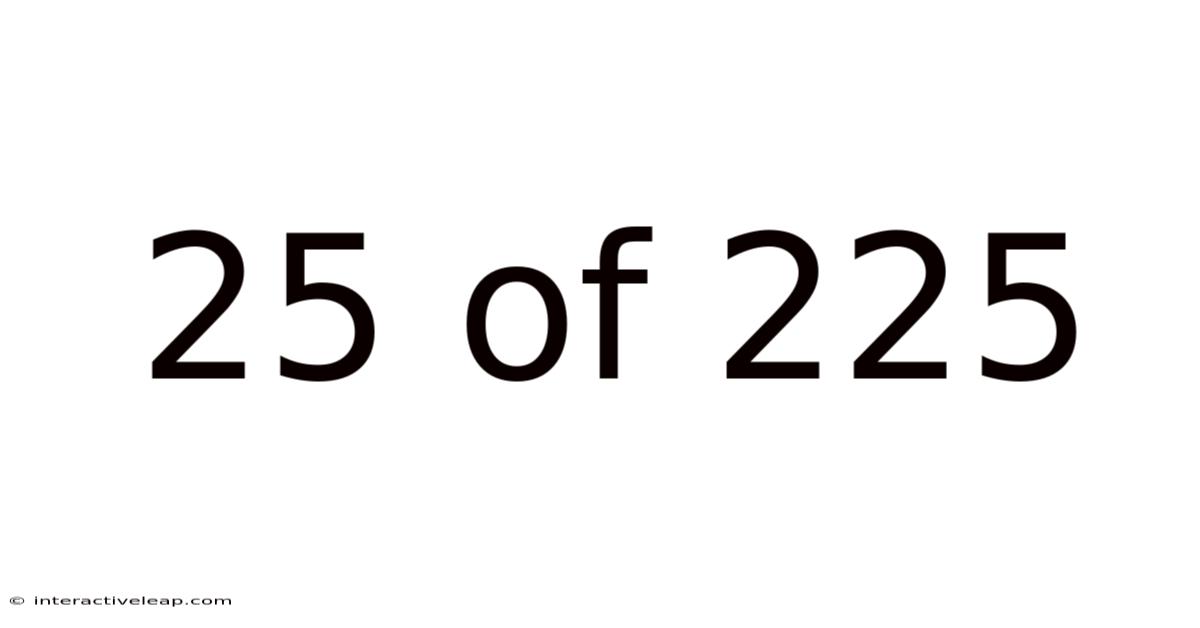
Table of Contents
Decoding the Fraction: Understanding 25/225 and its Implications
The seemingly simple fraction 25/225 might appear insignificant at first glance. However, understanding this fraction, its simplification, and its broader implications within mathematics and beyond opens up a world of numerical relationships and problem-solving techniques. This article delves deep into the analysis of 25/225, exploring its simplification, practical applications, and the underlying mathematical concepts involved. We will cover everything from basic fraction reduction to exploring its representation in decimal form and its relevance in various fields.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The cornerstone of working with fractions lies in simplification. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator share no common factors other than 1. To simplify 25/225, we need to find the greatest common divisor (GCD) of 25 and 225.
The GCD is the largest number that divides both 25 and 225 without leaving a remainder. One method to find the GCD is through prime factorization.
- Prime Factorization of 25: 5 x 5 = 5²
- Prime Factorization of 225: 3 x 3 x 5 x 5 = 3² x 5²
By comparing the prime factorizations, we can see that the common factors are 5² (or 25). Therefore, the GCD of 25 and 225 is 25.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
25 ÷ 25 = 1 225 ÷ 25 = 9
Therefore, 25/225 simplifies to 1/9. This simplified fraction is equivalent to the original fraction but is expressed in its most concise form.
Visualizing the Fraction: A Geometric Perspective
Understanding fractions can be significantly enhanced by visualizing them. Imagine a square divided into nine equal parts. The fraction 1/9 represents one of these nine parts. Similarly, the fraction 25/225, before simplification, would represent 25 of these same nine parts. This visual representation helps illustrate the equivalence between the two fractions – 25 out of 225 is the same as 1 out of 9.
Converting to Decimal: Expressing the Fraction as a Decimal Number
Fractions and decimals are two different ways of representing the same numerical value. To convert the simplified fraction 1/9 to a decimal, we perform the division:
1 ÷ 9 = 0.11111...
The result is a repeating decimal, denoted as 0.¯¯1. The bar above the 1 indicates that the digit 1 repeats infinitely. This emphasizes that fractions and decimals, while different in form, express the same proportional relationship.
Practical Applications of Fractions: Real-world Examples
Fractions are not just abstract mathematical concepts; they are integral to numerous aspects of daily life. Here are some examples where understanding 25/225 (and its simplified form 1/9) could be relevant:
-
Percentage Calculation: The fraction 1/9 can easily be converted to a percentage by multiplying by 100: (1/9) * 100 ≈ 11.11%. This is useful for calculating discounts, tax rates, or representing proportions in various contexts.
-
Ratio and Proportion: If you have 25 apples out of a total of 225 fruits, the ratio of apples to the total number of fruits is 25:225, which simplifies to 1:9. This ratio is useful for comparing quantities and understanding proportions.
-
Measurement and Units: Imagine dividing a 225-meter track into segments. 25 meters would represent 1/9 of the entire track's length.
-
Probability: If there is a 1/9 chance of a specific event occurring, this could be visualized as having 25 successful outcomes out of 225 attempts.
-
Recipe Scaling: If a recipe calls for 25 grams of an ingredient in a total recipe of 225 grams, you could simplify the ratio to 1/9 and easily scale the recipe up or down.
Further Exploration: Beyond Simple Fractions
While 25/225 provides a straightforward example, understanding the concepts of simplifying fractions and converting them to decimals is crucial for tackling more complex fractions and mathematical operations. This foundational knowledge is vital for further studies in:
- Algebra: Solving equations involving fractions.
- Calculus: Working with limits, derivatives, and integrals.
- Geometry: Calculating areas, volumes, and proportions.
- Statistics: Working with probabilities and proportions.
Frequently Asked Questions (FAQs)
-
Q: What is the simplest form of 25/225?
- A: The simplest form is 1/9.
-
Q: How do you simplify a fraction?
- A: Find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
-
Q: What is a repeating decimal?
- A: A repeating decimal is a decimal number where one or more digits repeat infinitely.
-
Q: Can all fractions be converted to decimals?
- A: Yes, all fractions can be converted to decimals by dividing the numerator by the denominator. The resulting decimal may be terminating (ending) or repeating.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and work with in further calculations.
Conclusion: The Significance of Simplicity
The fraction 25/225, although seemingly simple, serves as a powerful example of the fundamental principles of fraction simplification, decimal conversion, and practical application within mathematics. By mastering these fundamental concepts, we equip ourselves with essential tools for problem-solving in numerous fields, ranging from everyday tasks to complex scientific calculations. The journey from 25/225 to its simplified form 1/9 highlights the beauty and elegance of mathematical simplification – the power of expressing complex relationships in their most concise and understandable forms. This understanding forms a crucial foundation for more advanced mathematical concepts and problem-solving skills. The seemingly small step of simplifying a fraction is, in essence, a giant leap towards a deeper comprehension of the mathematical world.
Latest Posts
Latest Posts
-
30 Of 420
Sep 20, 2025
-
Aut Cursed Orb
Sep 20, 2025
-
50 Off 40
Sep 20, 2025
-
70 Of 210
Sep 20, 2025
-
25 Of 100000
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 225 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.