25 Of 100000
interactiveleap
Sep 20, 2025 · 5 min read
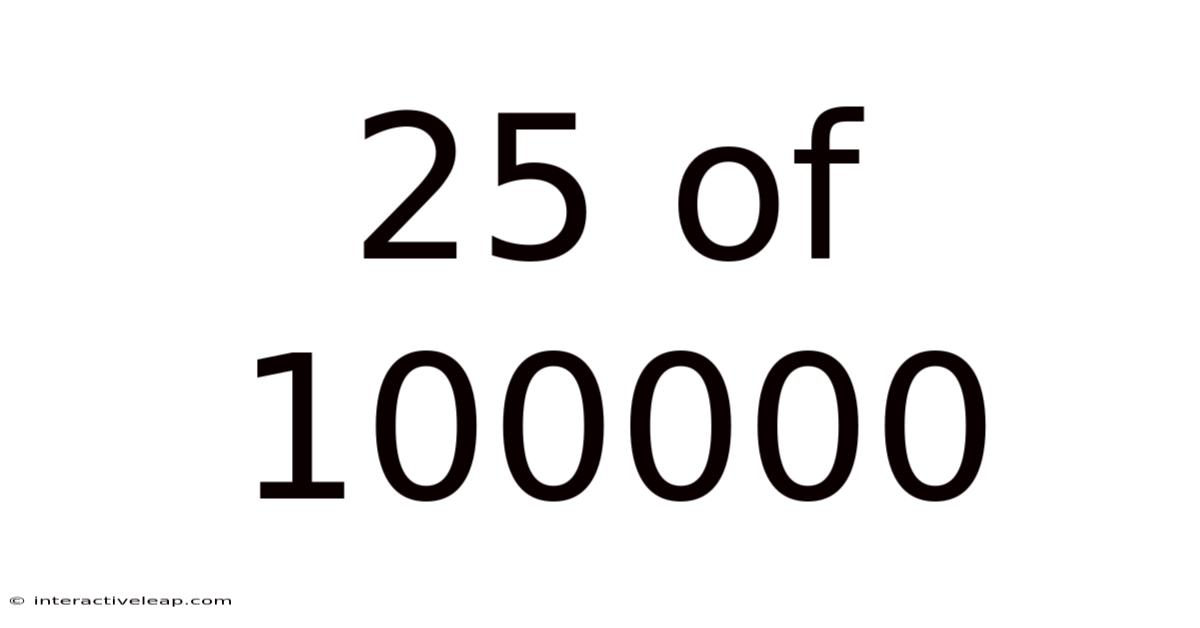
Table of Contents
Decoding the Infinitesimal: Exploring the Significance of 25 out of 100,000
Understanding the relationship between seemingly small numbers and larger contexts is crucial in various fields, from statistics and probability to finance and public health. This article delves into the meaning and implications of the fraction 25/100,000, exploring its mathematical representation, practical applications, and the broader concepts it illustrates. We'll look at how to interpret this fraction, its percentage equivalent, and the importance of contextualizing such small proportions. Understanding these concepts can improve decision-making in numerous scenarios, from evaluating risk to interpreting scientific data.
Understanding the Fraction: 25/100,000
At first glance, 25/100,000 might seem insignificant. However, the value of this fraction depends entirely on the context in which it's presented. Mathematically, it represents a ratio: 25 parts out of a total of 100,000 parts. This fraction can be simplified by dividing both the numerator and denominator by 25, resulting in 1/4000. This simpler form makes it easier to visualize the proportion.
Converting to Percentage: A More Intuitive Representation
While the fraction form is precise, percentages often offer a more intuitive understanding. To convert 25/100,000 to a percentage, we divide the numerator by the denominator and multiply by 100:
(25 / 100,000) * 100 = 0.025%
This reveals that 25 out of 100,000 represents a very small percentage – just 0.025%. This small percentage highlights the relative insignificance of the number 25 when compared to the much larger total of 100,000. However, the impact of this small percentage can be substantial depending on the context.
Context Matters: Real-World Applications and Implications
The significance of 25 out of 100,000 is highly dependent on the context. Let's examine several scenarios:
Scenario 1: Public Health – Disease Prevalence
Imagine 25 cases of a rare disease are reported in a population of 100,000. While 0.025% might seem negligible, in public health, even a small prevalence rate can be concerning, especially if the disease is severe or fatal. Public health officials would investigate the cause of the outbreak, implement preventative measures, and monitor the situation closely. The small percentage doesn't diminish the seriousness of the situation for those affected.
Scenario 2: Manufacturing – Defect Rate
In a manufacturing process, 25 defective items out of 100,000 produced might represent an acceptable defect rate for some companies. However, others might consider this unacceptable and implement measures to improve quality control. The acceptable defect rate depends on various factors, including the cost of fixing defects, the potential consequences of faulty products, and the industry standards.
Scenario 3: Financial Markets – Investment Returns
In the context of investment returns, 25 out of 100,000 might represent a minuscule gain or loss. However, when multiplied by the total investment amount, even a small percentage can result in a significant monetary change. Understanding such small percentage changes is crucial for long-term investment strategies and risk management.
Scenario 4: Scientific Research – Statistical Significance
In scientific research, a finding might be considered statistically significant even if it involves a small proportion. For example, a clinical trial might show a 0.025% increase in positive outcomes in a treatment group compared to a control group. While seemingly small, statistical tests can determine if this difference is significant enough to rule out chance and conclude that the treatment is effective. The statistical significance hinges on factors like sample size, effect size, and the chosen significance level.
Beyond the Numbers: Understanding Statistical Concepts
The fraction 25/100,000 highlights several important statistical concepts:
-
Relative Frequency: This fraction represents the relative frequency of an event—in this case, 25 occurrences out of 100,000 total observations.
-
Probability: The fraction can also be interpreted as an estimate of the probability of the event occurring (approximately 0.00025). This probability represents the likelihood of the event happening in a single trial.
-
Sample Size: The denominator (100,000) represents the sample size. Larger sample sizes generally lead to more reliable estimates of population parameters.
-
Statistical Inference: When working with a sample (like 100,000 individuals), we often use statistical inference to make inferences about a larger population. Understanding the precision of our sample estimate is vital to draw accurate conclusions.
Frequently Asked Questions (FAQs)
Q1: How do I calculate the percentage from a fraction?
To calculate the percentage from a fraction, divide the numerator by the denominator and then multiply the result by 100. For example, (25/100,000) * 100 = 0.025%.
Q2: Is 25/100,000 a significant number?
The significance of 25/100,000 depends entirely on the context. In some situations, it might be considered negligible, while in others, it could be highly significant.
Q3: What are some other ways to represent 25/100,000?
Besides percentage and simplified fraction (1/4000), you can represent it as a decimal (0.00025) or in scientific notation (2.5 x 10^-4).
Q4: How can I improve my understanding of statistical concepts?
To improve your understanding of statistical concepts, consider taking introductory statistics courses or reading textbooks and online resources on the subject. Practicing solving problems related to proportions, percentages, and probabilities is also essential.
Conclusion: The Power of Context and Critical Thinking
The seemingly insignificant fraction 25/100,000 holds more depth than a simple numerical calculation suggests. Its interpretation depends heavily on the context in which it is presented. Understanding how to convert between fractions, percentages, and decimals, and recognizing the importance of sample size and statistical significance are crucial skills for anyone dealing with numerical data. By developing a strong foundation in these concepts, we can critically analyze information and make informed decisions in various fields. The seemingly small can hold significant implications, highlighting the need for careful analysis and contextual understanding in interpreting numerical data. Remember, the ability to correctly interpret even small numerical proportions is a valuable asset in navigating the complexities of the modern world.
Latest Posts
Latest Posts
-
60 Of 6
Sep 20, 2025
-
Lockwood Wuthering Heights
Sep 20, 2025
-
The Broken Chain
Sep 20, 2025
-
20 Of 315
Sep 20, 2025
-
124m In Cm
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 100000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.