70 Of 210
interactiveleap
Sep 20, 2025 · 5 min read
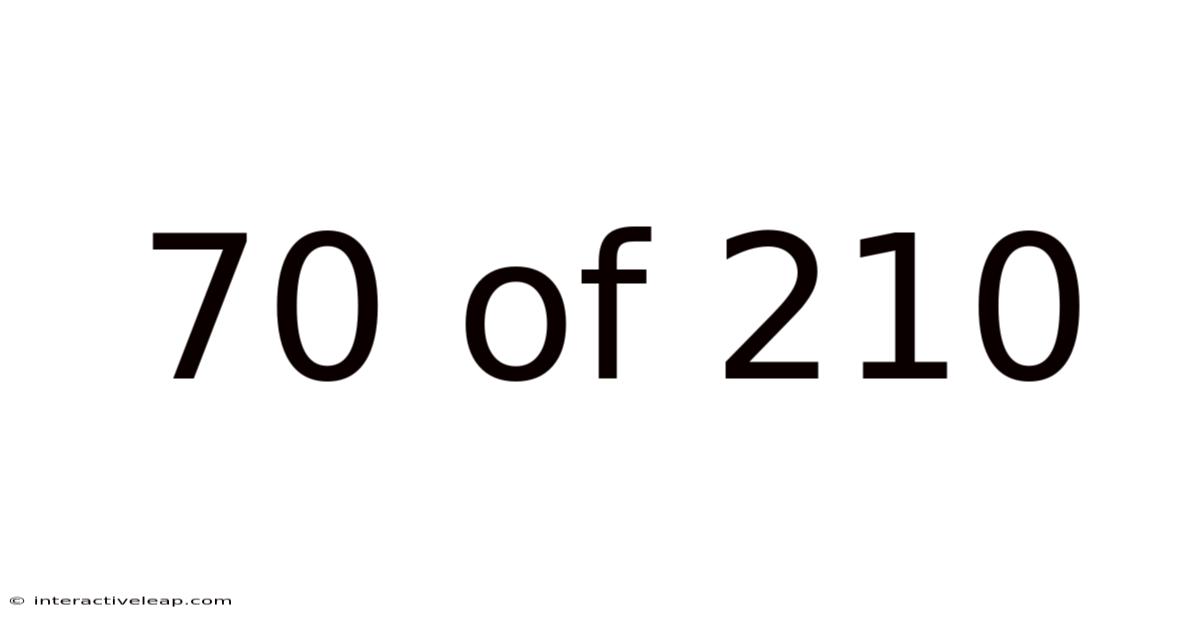
Table of Contents
Decoding the Fraction: Understanding 70/210 and its Implications
What does 70/210 truly represent? This seemingly simple fraction hides a wealth of mathematical concepts and practical applications. This article will delve deep into the meaning of 70/210, exploring its simplification, decimal equivalent, percentage representation, and real-world applications. We'll also explore related mathematical concepts and answer frequently asked questions, making this a comprehensive guide for students, educators, and anyone curious about fractions.
Introduction: Unveiling the Fraction's Secrets
The fraction 70/210, at first glance, might seem daunting. However, understanding its core components – the numerator (70) and the denominator (210) – is the key to unlocking its meaning. The numerator represents the part we're interested in, while the denominator represents the whole. In essence, 70/210 signifies 70 parts out of a total of 210 parts. This article will explore how we can simplify this fraction, convert it to other forms, and ultimately understand its value and implications in various contexts. We will also cover the fundamental concepts of fractions, simplification, and percentage conversions to ensure a solid understanding for all readers.
Simplifying the Fraction: Finding the Lowest Terms
One of the most crucial steps in working with fractions is simplification. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator share no common factors other than 1. This process makes the fraction easier to understand and work with. To simplify 70/210, we need to find the greatest common divisor (GCD) of 70 and 210.
The prime factorization method is a useful tool here. Let's break down both numbers into their prime factors:
- 70 = 2 x 5 x 7
- 210 = 2 x 3 x 5 x 7
By comparing the prime factorizations, we can see that the common factors are 2, 5, and 7. Therefore, the GCD of 70 and 210 is 2 x 5 x 7 = 70.
Now, we can simplify the fraction by dividing both the numerator and the denominator by the GCD:
70/210 = (70 ÷ 70) / (210 ÷ 70) = 1/3
Therefore, the simplified form of 70/210 is 1/3. This simplified fraction is much easier to visualize and use in calculations.
Converting to Decimal: Understanding the Numerical Value
Converting a fraction to its decimal equivalent is another important skill. To convert 1/3 to a decimal, we simply divide the numerator (1) by the denominator (3):
1 ÷ 3 = 0.3333...
The result is a repeating decimal, indicated by the ellipsis (...). This means the digit 3 repeats infinitely. For practical purposes, we often round this to a certain number of decimal places, such as 0.33 or 0.333.
Expressing as a Percentage: A Practical Representation
Percentages are a common way of expressing fractions, particularly in real-world applications. To convert a fraction to a percentage, we multiply the decimal equivalent by 100:
0.3333... x 100 = 33.333...%
Again, we often round this to a specific number of decimal places, such as 33.33% or 33.3%. This percentage representation provides a readily understandable measure of the proportion represented by the fraction.
Real-World Applications: Seeing Fractions in Action
Fractions like 70/210, and its simplified form 1/3, are ubiquitous in everyday life. Here are a few examples:
- Cooking: If a recipe calls for 210 grams of flour and you only want to make 1/3 of the recipe, you would use 70 grams (70/210 = 1/3).
- Measurements: If you have a 210-meter-long piece of fabric and need a piece that's 1/3 of the total length, you would need a 70-meter piece.
- Probability: If there are 210 possible outcomes in an event and 70 of those outcomes are favorable, the probability of a favorable outcome is 70/210, or 1/3.
- Discounts: A store offers a 1/3 discount on an item, meaning you pay only 2/3 of the original price.
- Data Analysis: In data analysis, 70/210 might represent the proportion of a sample that possesses a certain characteristic.
These examples highlight the practical relevance of understanding fractions, demonstrating their applicability across diverse fields.
Expanding on Mathematical Concepts: Beyond the Basics
Understanding 70/210 allows us to explore related mathematical concepts:
- Equivalent Fractions: Any fraction that simplifies to 1/3 is equivalent to 70/210. For example, 2/6, 3/9, 10/30, and countless others are equivalent.
- Ratio and Proportion: The fraction 70/210 can be expressed as a ratio of 70:210, which simplifies to 1:3. This signifies a proportional relationship where one quantity is one-third of the other.
- Improper Fractions and Mixed Numbers: While 70/210 is a proper fraction (numerator < denominator), if the fraction were reversed (210/70), it would be an improper fraction. Improper fractions can be converted into mixed numbers (a whole number and a proper fraction).
Frequently Asked Questions (FAQ)
-
Q: How can I simplify other fractions? A: Find the greatest common divisor (GCD) of the numerator and denominator using prime factorization or other methods, then divide both by the GCD.
-
Q: What if the fraction has a decimal in the numerator or denominator? A: Convert the decimal to a fraction first, then find a common denominator and simplify.
-
Q: Are there any online tools to simplify fractions? A: Yes, many websites and calculators are available to simplify fractions quickly and easily.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also reduces the risk of errors in calculations.
Conclusion: Mastering Fractions for a Brighter Future
Understanding the fraction 70/210, its simplification to 1/3, and its various representations is a fundamental skill with broad applications. This article has provided a comprehensive exploration of this seemingly simple fraction, demonstrating its significance in various mathematical contexts and real-world scenarios. By grasping the concepts discussed here, you will gain a stronger foundation in mathematics and improve your problem-solving abilities across various disciplines. Remember, the key to mastering fractions lies in understanding the underlying principles of simplification, conversion, and the practical implications of these mathematical tools. Whether you're a student striving for academic excellence or an adult navigating daily life, a solid grasp of fractions will empower you to tackle a wide array of challenges with confidence. The journey to mastering fractions may seem daunting at times, but with consistent effort and a clear understanding of the fundamentals, you will inevitably reach a point where you can confidently navigate the world of numbers and their practical applications.
Latest Posts
Latest Posts
-
60 Of 6
Sep 20, 2025
-
Lockwood Wuthering Heights
Sep 20, 2025
-
The Broken Chain
Sep 20, 2025
-
20 Of 315
Sep 20, 2025
-
124m In Cm
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 210 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.