25 Of 1200
interactiveleap
Sep 15, 2025 · 6 min read
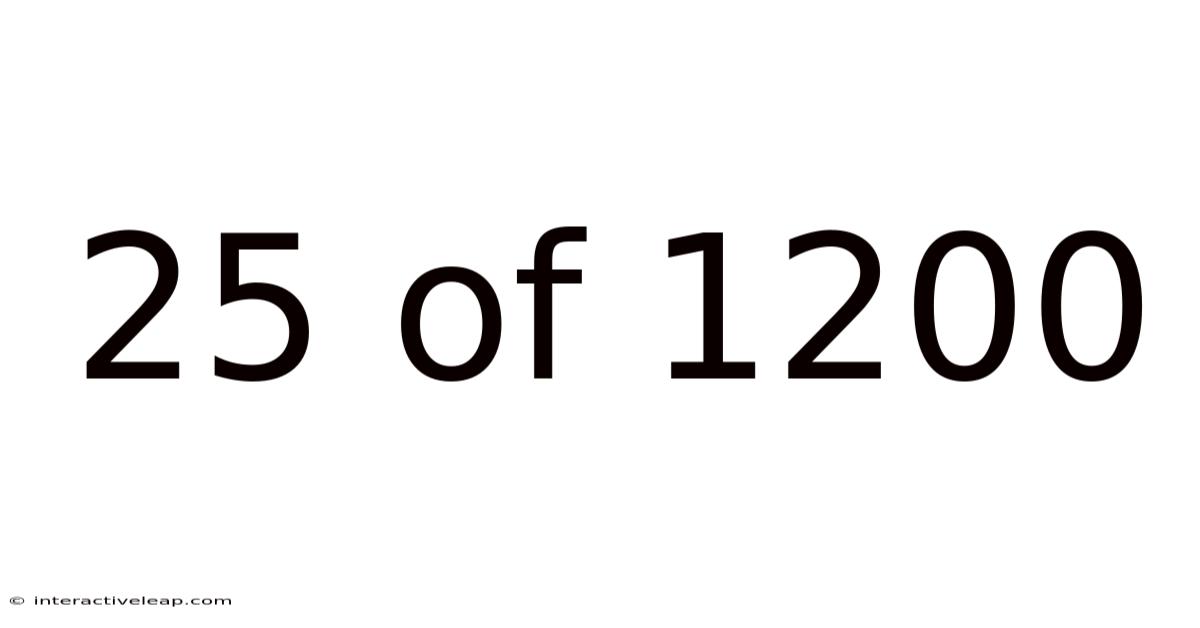
Table of Contents
Decoding the Fraction: Understanding 25 out of 1200
The seemingly simple fraction 25/1200 represents a common challenge in understanding proportions and percentages. Whether you're analyzing data, calculating success rates, or simply trying to grasp the relative size of a part to a whole, understanding how to interpret and work with such fractions is crucial. This article will delve into the various ways to understand 25 out of 1200, providing practical methods and explanations that will build your confidence in tackling similar fractional problems.
Introduction: Why Understanding Fractions Matters
Fractions are the fundamental building blocks of many mathematical concepts. They represent parts of a whole and are essential in various fields, from finance and statistics to engineering and everyday life. Understanding how to simplify, compare, and convert fractions into percentages and decimals is a crucial skill. This article will focus specifically on the fraction 25/1200, showing you multiple approaches to comprehend its meaning and implications. We'll move beyond simple calculations and explore the underlying principles, helping you develop a deeper understanding of proportional reasoning.
1. Simplifying the Fraction:
The first step in understanding 25/1200 is to simplify it to its lowest terms. This makes the fraction easier to interpret and work with. Both the numerator (25) and the denominator (1200) are divisible by 25.
- Step 1: Divide both the numerator and the denominator by 25:
25 ÷ 25 = 1 1200 ÷ 25 = 48
- Simplified Fraction: This simplifies the fraction to 1/48. This means 25 out of 1200 is equivalent to 1 out of 48. This simplified form provides a clearer, more concise representation of the proportion.
2. Converting to a Percentage:
Converting a fraction to a percentage provides a readily understandable representation of the proportion. To do this, we divide the numerator by the denominator and then multiply by 100.
- Using the simplified fraction (1/48):
1 ÷ 48 ≈ 0.020833...
0.020833... × 100 ≈ 2.08%
- Using the original fraction (25/1200):
25 ÷ 1200 ≈ 0.020833...
0.020833... × 100 ≈ 2.08%
Therefore, 25 out of 1200 represents approximately 2.08%. This percentage clearly shows that 25 is a relatively small portion of 1200.
3. Visual Representation: Understanding the Proportion
Visualizing the fraction can significantly improve understanding. Imagine you have 1200 marbles, and 25 of them are red. The fraction 25/1200 represents the proportion of red marbles to the total number of marbles. To visualize this, consider dividing the 1200 marbles into 48 equal groups. Each group would contain 25 marbles. Out of these 48 groups, only one group would contain all the red marbles. This visual representation helps to contextualize the numerical representation.
4. Real-World Applications: Contextualizing the Fraction
The fraction 25/1200 can be applied in various real-world scenarios. For example:
- Test Scores: If a student answered 25 questions correctly out of 1200 questions on a large exam, their score would be approximately 2.08%.
- Survey Results: If 25 out of 1200 respondents to a survey answered "yes" to a particular question, the percentage of "yes" responses would be approximately 2.08%.
- Manufacturing Defects: If a factory produces 1200 products and 25 of them are defective, the defect rate is approximately 2.08%.
- Statistical Analysis: In statistical analysis, this fraction could represent a small sample size compared to a larger population. Understanding the relative size of this sample is crucial for interpreting results.
These examples highlight the importance of understanding how to interpret and utilize fractions in various contexts. The ability to quickly calculate and interpret such proportions is a valuable skill in numerous fields.
5. Comparing Fractions: Relative Sizes
Understanding the relative size of fractions is critical when comparing different proportions. For example, comparing 25/1200 to another fraction, such as 50/1200, is straightforward. 50/1200 is double 25/1200, representing a significantly larger proportion (approximately 4.17%).
6. Advanced Concepts: Ratios and Proportions
The fraction 25/1200 can also be expressed as a ratio: 25:1200. Ratios and proportions are closely related concepts. A proportion is a statement that two ratios are equal. Understanding these concepts allows you to solve problems involving proportional relationships. For instance, if the ratio of red marbles to blue marbles is 25:1200, and you have 50 red marbles, you can use proportions to determine the number of blue marbles.
7. Error Analysis and Precision:
It's important to note that when converting fractions to decimals or percentages, rounding may introduce slight inaccuracies. The decimal representation of 25/1200 is approximately 0.0208333..., which is often rounded to 2.08%. However, it is crucial to remember that this is an approximation. Depending on the context, the level of precision required may vary. In some scientific or engineering applications, more decimal places might be necessary for accuracy.
8. Working with Larger Numbers:
The principles discussed here apply to fractions with even larger numbers. For instance, imagine you have 25,000 items out of 1,200,000. The simplified fraction would still be 1/48, and the percentage would remain approximately 2.08%. This consistency highlights the fundamental importance of simplifying fractions to understand the underlying proportion.
9. Frequently Asked Questions (FAQ)
- Q: How do I calculate the percentage without a calculator?
A: While a calculator makes the process easier, you can perform long division to divide the numerator by the denominator and then multiply by 100. Alternatively, you can use the simplified fraction and perform the division on the smaller numbers.
- Q: Why is simplifying the fraction important?
A: Simplifying makes the fraction easier to understand and work with. It provides a clearer representation of the proportion and simplifies further calculations.
- Q: What if the numbers are not easily divisible?
A: If the numerator and denominator don't share common factors easily identifiable, you can use prime factorization to find the greatest common divisor (GCD) and simplify the fraction accordingly.
- Q: Are there any online tools to help with fraction calculations?
A: Many websites and apps are available online to assist with fraction simplification, conversion to percentages, and other related calculations.
- Q: How can I improve my understanding of fractions?
A: Practice is key. Work through various problems, starting with simple fractions and gradually increasing the complexity. Visual aids and real-world examples can also be helpful in improving comprehension.
10. Conclusion: Mastering Fractions for a Deeper Understanding
Understanding the fraction 25/1200, and fractions in general, is not just about performing calculations. It's about developing a deeper understanding of proportions, ratios, and percentages. By mastering these fundamental concepts, you equip yourself with essential tools for problem-solving across various disciplines and everyday scenarios. The ability to simplify, convert, and visualize fractions allows you to interpret data effectively and communicate your findings clearly. The methods and explanations provided in this article provide a solid foundation for developing your proficiency in handling fractions and their applications in a variety of contexts. Remember that consistent practice and a focus on understanding the underlying principles are crucial to mastering this fundamental mathematical concept.
Latest Posts
Latest Posts
-
20 Of 460
Sep 15, 2025
-
115 Lb Kg
Sep 15, 2025
-
75 Of 200
Sep 15, 2025
-
52 4kg In Stone
Sep 15, 2025
-
30 Of 27
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.