75 Of 200
interactiveleap
Sep 15, 2025 · 6 min read
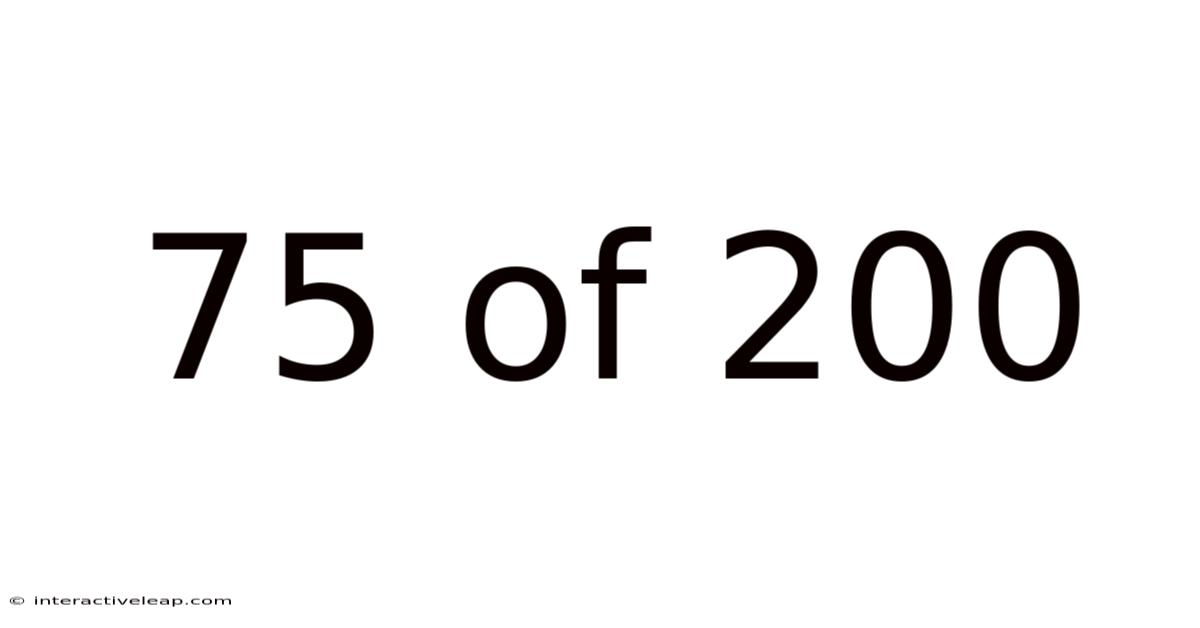
Table of Contents
Decoding the Fraction: 75/200 – A Deep Dive into Simplification and Applications
Understanding fractions is a fundamental skill in mathematics, crucial for various aspects of life, from baking a cake to understanding financial reports. This article delves into the specific fraction 75/200, exploring its simplification, equivalent fractions, decimal and percentage representations, and real-world applications. We'll uncover the underlying mathematical principles and provide practical examples to solidify your comprehension. By the end, you'll not only know how to simplify 75/200 but also understand the broader concepts involved in working with fractions.
Simplifying 75/200: Finding the Greatest Common Divisor (GCD)
The fraction 75/200 represents 75 parts out of a total of 200 parts. To simplify this fraction, we need to find the greatest common divisor (GCD) of both the numerator (75) and the denominator (200). The GCD is the largest number that divides both numbers without leaving a remainder.
One way to find the GCD is through prime factorization. Let's break down 75 and 200 into their prime factors:
- 75 = 3 x 5 x 5
- 200 = 2 x 2 x 2 x 5 x 5
Comparing the prime factorizations, we see that both numbers share two factors of 5. Therefore, the GCD of 75 and 200 is 5 x 5 = 25.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
75 ÷ 25 = 3 200 ÷ 25 = 8
Therefore, the simplified fraction is 3/8. This means that 75/200 and 3/8 represent the same value; they are equivalent fractions.
Equivalent Fractions: Exploring Different Representations
Understanding equivalent fractions is crucial for flexibility in mathematical operations. Any fraction can be expressed in infinitely many equivalent forms by multiplying or dividing both the numerator and the denominator by the same non-zero number. For instance:
- Multiplying by 2: (3/8) x (2/2) = 6/16
- Multiplying by 3: (3/8) x (3/3) = 9/24
- Multiplying by 4: (3/8) x (4/4) = 12/32
And so on. All these fractions – 6/16, 9/24, 12/32, and so on – are equivalent to 3/8 and, therefore, also equivalent to the original fraction 75/200. The simplified form, 3/8, is preferred for its simplicity and ease of use in calculations.
Converting to Decimal and Percentage: Practical Applications
Converting fractions to decimals and percentages is essential for practical applications. To convert 3/8 to a decimal, we simply divide the numerator (3) by the denominator (8):
3 ÷ 8 = 0.375
Therefore, the decimal representation of 75/200 (and 3/8) is 0.375.
To convert the decimal to a percentage, we multiply by 100:
0.375 x 100 = 37.5%
So, 75/200 is equivalent to 37.5%. This percentage representation is widely used in various contexts, such as expressing discounts, calculating interest rates, and representing proportions in data analysis.
Real-World Applications of 75/200 (and 3/8)
The fraction 75/200, and its simplified form 3/8, appears in numerous real-world situations. Here are a few examples:
-
Proportions and Ratios: Imagine a survey where 75 out of 200 respondents answered "yes" to a particular question. The fraction 75/200 (or 3/8) represents the proportion of "yes" responses. This allows for easy comparison with other survey results or the calculation of percentages.
-
Measurements and Units: Consider a recipe that calls for 75 grams of sugar in a 200-gram cake. The fraction 75/200 (or 3/8) shows that sugar constitutes 37.5% of the cake's total weight. This is helpful in scaling recipes up or down.
-
Probability and Statistics: In a game of chance, if there are 200 possible outcomes and 75 of them are favorable, the probability of a favorable outcome is 75/200 (or 3/8), which is 37.5%. This is a fundamental concept in probability theory.
-
Financial Calculations: Suppose you invest $200 and earn a profit of $75. The fraction 75/200 (or 3/8) represents your return on investment (ROI) as a fraction. Converting this to a percentage (37.5%) provides a clearer understanding of your investment's performance.
Beyond Simplification: Working with Fractions in General
While simplifying 75/200 to 3/8 is a valuable skill, it's important to understand the broader context of working with fractions. Here are some key concepts:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
-
Multiplying Fractions: Multiplying fractions is straightforward: Multiply the numerators together and multiply the denominators together. Simplification often follows multiplication.
-
Dividing Fractions: To divide fractions, invert the second fraction (reciprocal) and then multiply.
-
Mixed Numbers: A mixed number contains a whole number and a fraction (e.g., 1 3/8). To perform calculations, it's often helpful to convert mixed numbers into improper fractions (where the numerator is larger than the denominator).
Frequently Asked Questions (FAQ)
Q1: Are there other ways to simplify 75/200 besides using prime factorization?
A1: Yes, you can use the Euclidean algorithm to find the GCD. This algorithm involves repeatedly dividing the larger number by the smaller number and taking the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand and work with. It reduces the size of the numbers, making calculations simpler and reducing the risk of errors.
Q3: Can any fraction be simplified?
A3: Not all fractions can be simplified. If the numerator and denominator have no common factors other than 1, the fraction is already in its simplest form. This is often referred to as being in "lowest terms".
Q4: What if I get a decimal that doesn't terminate (e.g., 1/3 = 0.333...)?
A4: Some fractions, when converted to decimals, result in non-terminating, repeating decimals. This is perfectly acceptable. You can represent these decimals using a bar over the repeating digits (e.g., 0.3̅3̅).
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions, including simplifying fractions like 75/200, is a fundamental building block for success in mathematics and various real-world applications. Through simplification, we found that 75/200 is equivalent to the simpler fraction 3/8, which can be easily expressed as a decimal (0.375) and a percentage (37.5%). This knowledge empowers you to tackle various mathematical problems and interpret real-world data with greater confidence and precision. Remember the importance of equivalent fractions, the techniques for simplification, and the practical applications of this knowledge across diverse fields. By mastering these concepts, you are well-equipped to handle more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
80 8kg In Stone
Sep 15, 2025
-
98 9f To C
Sep 15, 2025
-
7 2 As Fraction
Sep 15, 2025
-
Sales Forecast Example
Sep 15, 2025
-
1 65 Kg Pounds
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.