24 X 1/6
interactiveleap
Sep 20, 2025 · 5 min read
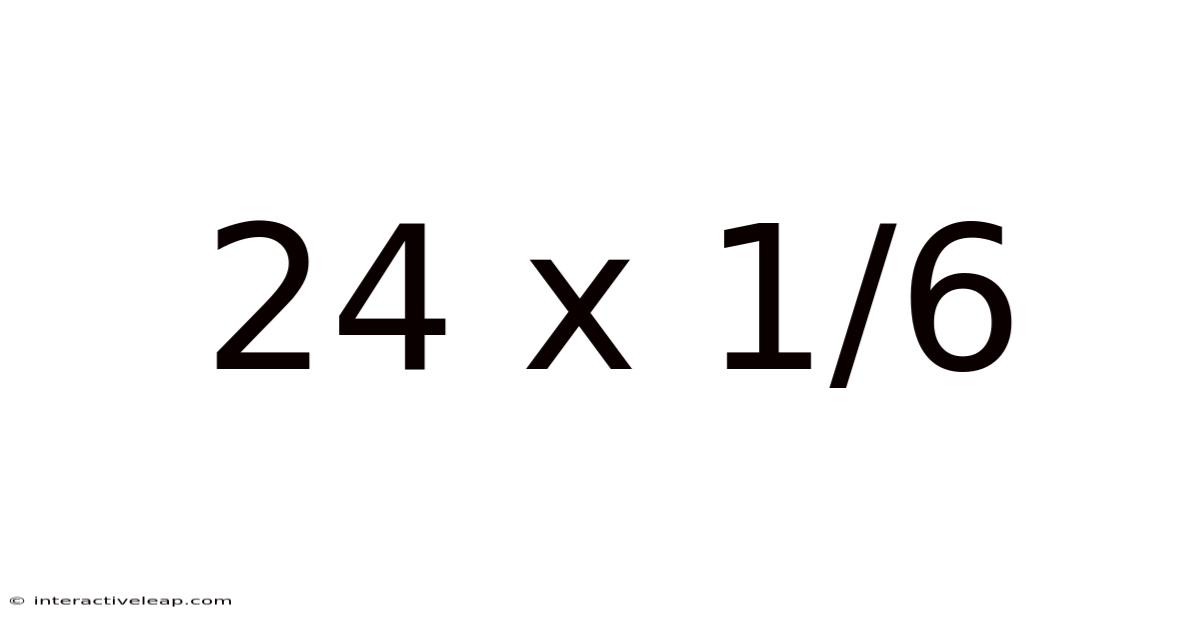
Table of Contents
Decoding 24 x 1/6: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can sometimes feel like navigating a maze. This article provides a comprehensive guide to solving 24 x 1/6, explaining the process step-by-step and exploring the underlying mathematical concepts. We'll cover various methods, delve into the practical applications, and answer frequently asked questions, ensuring you gain a solid grasp of this fundamental arithmetic operation. Whether you're a student brushing up on your skills or an adult looking to reinforce your mathematical foundation, this guide is designed to help you confidently tackle fraction multiplication problems.
Understanding Fractions: A Quick Refresher
Before diving into 24 x 1/6, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/6, the numerator is 1 and the denominator is 6. This means we have 1 part out of a total of 6 equal parts.
Method 1: Multiplying the Whole Number by the Numerator
The simplest approach to solving 24 x 1/6 is to multiply the whole number (24) by the numerator (1) and keep the denominator the same. This gives us:
24 x 1/6 = (24 x 1) / 6 = 24/6
This fraction, 24/6, represents 24 parts out of 6 equal parts. To simplify this, we divide the numerator by the denominator:
24 ÷ 6 = 4
Therefore, 24 x 1/6 = 4
Method 2: Converting the Whole Number to a Fraction
Another method involves converting the whole number into a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Thus, 24 can be written as 24/1. Now, we multiply the two fractions:
(24/1) x (1/6) = (24 x 1) / (1 x 6) = 24/6
Again, simplifying 24/6 gives us the answer: 4
Method 3: Using the Concept of "Of"
The multiplication of a whole number by a fraction can also be understood as finding a fraction of a whole number. In this case, we are finding 1/6 of 24. This means we're dividing 24 into 6 equal parts and taking one of those parts.
Dividing 24 by 6: 24 ÷ 6 = 4
This confirms that 1/6 of 24 is 4.
Visual Representation: Understanding the Concept
Imagine you have 24 cookies. You want to give 1/6 of them to a friend. To do this, you would divide the 24 cookies into 6 equal groups. Each group would contain 24 ÷ 6 = 4 cookies. Therefore, 1/6 of the cookies is 4 cookies. This visual representation helps solidify the concept behind the mathematical operation.
Mathematical Explanation: The Distributive Property
The multiplication of a whole number by a fraction is based on the distributive property of multiplication over addition. We can express 24 as the sum of its parts (e.g., 12 + 12, or 6 + 6 + 6 + 6). Then, we distribute the multiplication of 1/6 to each part:
(1/6) x (12 + 12) = (1/6) x 12 + (1/6) x 12 = 2 + 2 = 4
This demonstrates how the distributive property works, showing that multiplying the whole number by the fraction is equivalent to multiplying each part of the whole number by the fraction and then adding the results.
Extending the Concept: Multiplying Fractions by Fractions
The principles we've used for 24 x 1/6 can be extended to multiplying any fraction by another fraction. The general rule is:
(a/b) x (c/d) = (a x c) / (b x d)
Where 'a', 'b', 'c', and 'd' are integers, and 'b' and 'd' are not zero.
Practical Applications of Fraction Multiplication
Fraction multiplication is a fundamental concept with numerous real-world applications:
- Cooking and Baking: Scaling recipes up or down requires fraction multiplication. If a recipe calls for 1/2 cup of flour and you want to double the recipe, you would multiply 1/2 by 2.
- Construction and Engineering: Accurate measurements and calculations in construction often involve fractions.
- Finance and Budgeting: Calculating percentages, interest rates, and discounts frequently involves fractions.
- Data Analysis: Understanding proportions and ratios in data analysis relies heavily on the ability to work with fractions.
Frequently Asked Questions (FAQ)
Q: What if the whole number is not divisible by the denominator?
A: Even if the whole number isn't perfectly divisible by the denominator, the process remains the same. You'll get a fraction as a result, which you can then simplify. For example: 10 x 1/3 = 10/3. This improper fraction can be converted to a mixed number: 3 1/3.
Q: Can I use a calculator to solve problems like 24 x 1/6?
A: Yes, most calculators can handle fraction multiplication. However, understanding the underlying mathematical concepts is crucial for problem-solving and for grasping more complex mathematical ideas.
Q: Are there other ways to approach fraction multiplication?
A: Yes, various methods exist, including using visual aids like area models or number lines to illustrate the process. The key is to find the method that best suits your understanding and makes the concept clear.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the answer easier to understand and interpret. It also makes further calculations more straightforward.
Q: What are improper fractions and mixed numbers?
A: An improper fraction is a fraction where the numerator is larger than the denominator (e.g., 24/6). A mixed number is a combination of a whole number and a proper fraction (e.g., 4).
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication opens doors to a deeper understanding of mathematics and its applications in various fields. While solving 24 x 1/6 may seem straightforward, grasping the underlying principles empowers you to tackle more complex problems with confidence. Remember, practice is key. The more you work with fractions, the more comfortable and proficient you will become. By understanding the different methods and visualizing the process, you'll not only solve problems accurately but also build a strong mathematical foundation for future learning.
Latest Posts
Latest Posts
-
Simplify 20 12
Sep 20, 2025
-
2 5 Of 25000
Sep 20, 2025
-
40l To Gallons
Sep 20, 2025
-
1 4 9
Sep 20, 2025
-
30 Of 57
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 24 X 1/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.