23 X 12
interactiveleap
Sep 15, 2025 · 6 min read
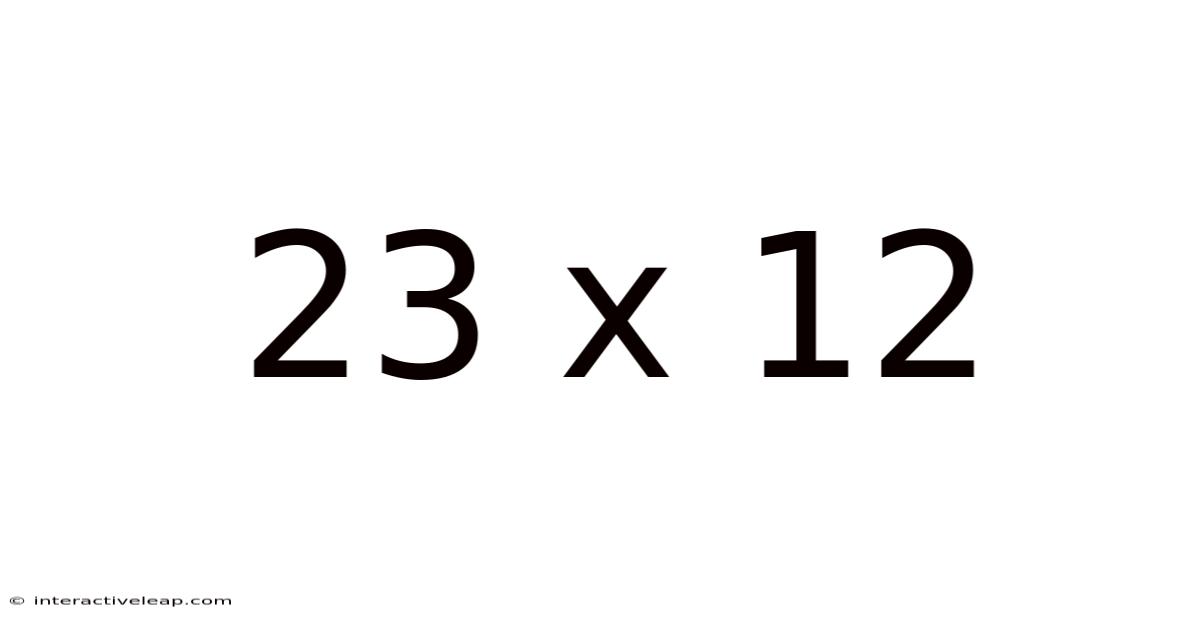
Table of Contents
Unveiling the Magic Behind 23 x 12: A Deep Dive into Multiplication and Beyond
The seemingly simple equation, 23 x 12, opens a door to a fascinating world of mathematical concepts, practical applications, and even a touch of historical context. This seemingly straightforward multiplication problem isn't just about finding the answer; it's about understanding the underlying principles and appreciating the power of numerical relationships. This article will explore the various methods to solve 23 x 12, delve into the history of multiplication, and illuminate the broader mathematical concepts connected to this seemingly simple calculation. We'll also address frequently asked questions and explore real-world applications to solidify your understanding.
Understanding the Fundamentals: Why 23 x 12 Matters
Before we jump into the calculations, it's important to understand why learning multiplication, and specifically 23 x 12, is significant. Multiplication is a fundamental building block of mathematics, crucial for everything from basic arithmetic to advanced calculus. Mastering multiplication techniques improves problem-solving skills, enhances critical thinking, and lays a strong foundation for future mathematical endeavors. Understanding 23 x 12 isn't just about getting the right answer; it's about understanding the process and the underlying principles.
Method 1: The Standard Algorithm (Long Multiplication)
The standard algorithm, also known as long multiplication, is a widely taught method for multiplying multi-digit numbers. This method breaks down the multiplication into smaller, manageable steps. Let's break down 23 x 12 step-by-step:
- Set up the problem: Write the numbers vertically, one above the other, aligning the units digits.
23
x 12
2. **Multiply by the units digit:** Multiply 23 by the units digit of 12 (which is 2).
23 x 12
46 (23 x 2 = 46)
3. **Multiply by the tens digit:** Multiply 23 by the tens digit of 12 (which is 1). Remember to add a zero as a placeholder in the units column because we are multiplying by 10.
23 x 12
46 230 (23 x 10 = 230)
4. **Add the partial products:** Add the results from steps 2 and 3.
23 x 12
46 230
276
Therefore, 23 x 12 = **276**.
### Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this property to solve 23 x 12:
1. **Break down the numbers:** Rewrite 23 as (20 + 3) and 12 as (10 + 2).
2. **Apply the distributive property:**
(20 + 3) x (10 + 2) = (20 x 10) + (20 x 2) + (3 x 10) + (3 x 2)
3. **Calculate:**
200 + 40 + 30 + 6 = **276**
### Method 3: The Lattice Method
The lattice method, while less commonly taught today, offers a visual approach to multiplication. It's particularly useful for larger numbers and can help visualize the process.
1. **Create the lattice:** Draw a grid with two rows (for the digits of 23) and two columns (for the digits of 12). Draw diagonals within each cell.
2. **Multiply and place the digits:** Multiply each digit of 23 by each digit of 12 and place the result in the corresponding cell, splitting the tens and units digits along the diagonal.
3. **Add the diagonals:** Add the numbers along each diagonal, carrying over to the next diagonal if necessary. The final answer is read from the bottom left to the top right.
*(Diagram of the lattice method would be included here in a visual format. Since this is text-based, a description is given instead)* The lattice would show the following: The top-left cell would contain "2" (from 2x1), the top-right cell "4" (from 2x2). The bottom-left cell would show "3" (from 3x1) and the bottom-right "6" (from 3x2). Adding the diagonals, starting from the bottom-right gives 6, then 3+4=7, then 2. This gives the answer 276.
### Method 4: Mental Math Techniques
With practice, you can develop mental math techniques to quickly solve 23 x 12. One approach is to break down the problem:
1. **Multiply by 10:** 23 x 10 = 230
2. **Multiply by 2:** 23 x 2 = 46
3. **Add the results:** 230 + 46 = **276**
### A Brief History of Multiplication
The concept of multiplication has ancient roots, evolving alongside human civilization's need for counting and measurement. Evidence suggests that early forms of multiplication were used in ancient Mesopotamia and Egypt as early as 2000 BC. The methods employed were often based on repeated addition or using multiplication tables. The development of more efficient algorithms, like the standard algorithm we use today, happened gradually over centuries, with significant contributions from various cultures and mathematicians.
### Real-World Applications of Multiplication
Understanding and mastering multiplication is essential in various real-world situations. Here are just a few examples:
* **Shopping:** Calculating the total cost of multiple items. For instance, if you buy 23 apples at $12 each, the total cost is 23 x $12 = $276.
* **Construction:** Calculating the area of a room or the amount of materials needed for a project. Imagine calculating the square footage of a room that's 23 feet by 12 feet.
* **Cooking:** Adjusting recipes based on the number of servings. Doubling a recipe often involves multiplying ingredient quantities.
* **Finance:** Calculating interest, discounts, or taxes. Understanding percentages and proportions relies heavily on multiplication.
* **Data Analysis:** Working with datasets and spreadsheets often involves multiplying values to find totals, averages, or other relevant figures.
### Exploring Further: Beyond 23 x 12
Understanding 23 x 12 provides a springboard to more complex mathematical concepts. It reinforces the fundamental principles of multiplication, lays the groundwork for algebra, and expands our ability to solve more complex problems. Consider exploring related concepts:
* **Factors and Multiples:** Identify the factors of 276 and understand its multiples.
* **Prime Factorization:** Break down 276 into its prime factors.
* **Divisibility Rules:** Use divisibility rules to quickly determine if 276 is divisible by certain numbers.
* **Algebraic Equations:** Use 23 x 12 as a basis for solving algebraic equations involving variables.
### Frequently Asked Questions (FAQs)
* **What is the easiest way to solve 23 x 12?** The easiest method depends on your individual preferences and mathematical strengths. The standard algorithm is widely taught, while the distributive property and mental math techniques offer alternative approaches.
* **Are there other methods to solve multiplication problems?** Yes, various methods exist, including the lattice method, Egyptian multiplication, and Russian peasant multiplication.
* **Why is learning multiplication important?** Multiplication is a fundamental skill crucial for numerous aspects of life, from everyday calculations to advanced academic pursuits.
* **How can I improve my multiplication skills?** Practice regularly, use different methods to reinforce your understanding, and explore online resources and educational games.
### Conclusion: Mastering the Fundamentals
The seemingly simple calculation of 23 x 12 serves as a microcosm of the broader mathematical world. By exploring different methods, understanding the historical context, and appreciating the real-world applications, we gain a deeper appreciation for the power and importance of multiplication. This journey beyond the simple answer emphasizes the importance of fundamental mathematical skills and their relevance in our daily lives. Continue to explore, practice, and discover the beauty and elegance of mathematics. The more you understand the underlying principles, the more confident and proficient you'll become in tackling even more challenging mathematical problems. Keep exploring, keep learning, and embrace the wonder of numbers!
Latest Posts
Latest Posts
-
52 4kg In Stone
Sep 15, 2025
-
30 Of 27
Sep 15, 2025
-
35 12
Sep 15, 2025
-
25oz To Grams
Sep 15, 2025
-
25 Of 230
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 23 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.