25 Of 230
interactiveleap
Sep 15, 2025 · 5 min read
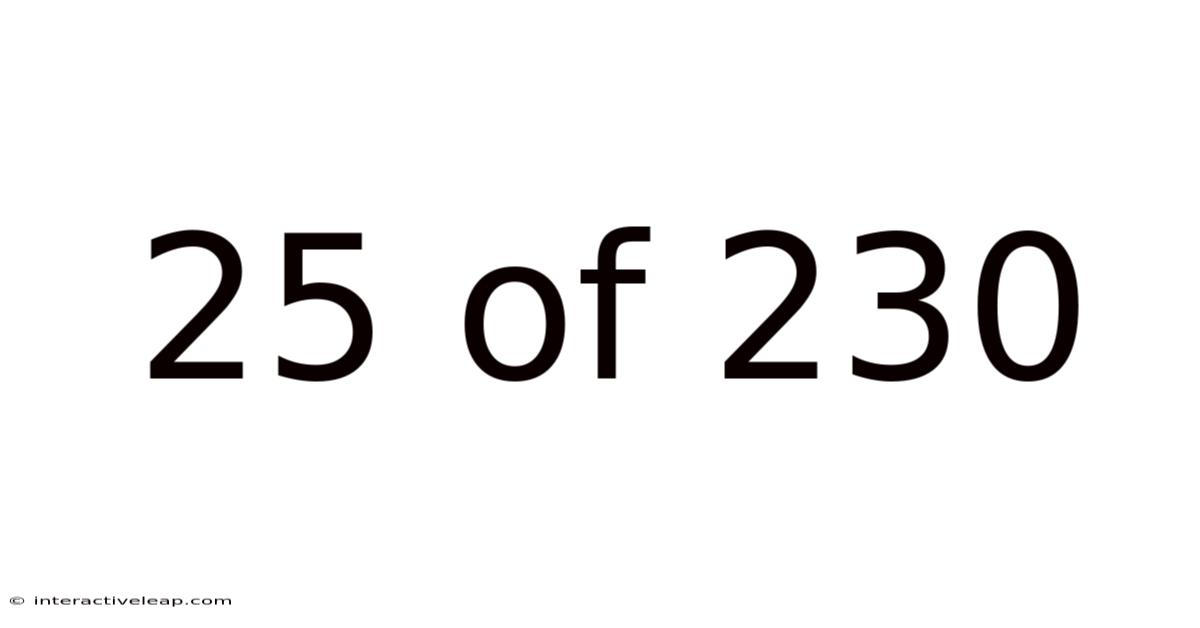
Table of Contents
Understanding the Fraction 25/230: A Comprehensive Guide
The fraction 25/230 might seem daunting at first glance, but understanding it is simpler than you might think. This article will provide a comprehensive guide to understanding this fraction, covering its simplification, decimal representation, percentage equivalent, and real-world applications. We'll also explore related mathematical concepts and answer frequently asked questions. By the end, you'll not only know what 25/230 represents but also possess a deeper understanding of fraction manipulation and its practical relevance.
Introduction: Deconstructing the Fraction 25/230
The fraction 25/230 represents a part of a whole. The numerator (25) indicates the number of parts we're considering, while the denominator (230) indicates the total number of equal parts the whole is divided into. This fraction, like many others, can be simplified to a more manageable form, making calculations and comprehension easier. Understanding fractions is fundamental to various mathematical operations and real-world applications, from calculating proportions to understanding percentages and ratios.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we dive into other representations, let's simplify 25/230. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 25 and 230, we can use the Euclidean algorithm or list the factors of each number.
- Factors of 25: 1, 5, 25
- Factors of 230: 1, 2, 5, 10, 23, 46, 115, 230
The greatest common factor of 25 and 230 is 5. Therefore, we divide both the numerator and the denominator by 5:
25 ÷ 5 = 5 230 ÷ 5 = 46
Thus, the simplified form of 25/230 is 5/46. This simplified fraction is equivalent to the original fraction, but it's easier to work with.
Decimal Representation: Converting the Fraction to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case, we'll divide 5 by 46:
5 ÷ 46 ≈ 0.10869565
This decimal representation shows that 25/230 (or 5/46) is approximately 0.1087. The decimal representation is particularly useful for comparing fractions or performing calculations involving decimals. Note that this is an approximate value because the decimal representation of 5/46 is a non-terminating, repeating decimal.
Percentage Equivalent: Expressing the Fraction as a Percentage
To express the fraction as a percentage, we multiply the decimal representation by 100:
0.10869565 × 100 ≈ 10.87%
Therefore, 25/230 is approximately 10.87%. Percentages are commonly used to represent proportions and are helpful in comparing different quantities expressed as fractions or decimals.
Real-World Applications: Understanding Proportions and Ratios
Fractions like 25/230 appear in various real-world scenarios. Imagine a scenario involving a survey:
- Scenario: A survey of 230 people found that 25 preferred a particular brand of coffee.
In this case, the fraction 25/230 (or its simplified form 5/46) represents the proportion of people who preferred that coffee brand. We can use this fraction to understand the popularity of the coffee brand relative to the total number of respondents. The percentage equivalent (approximately 10.87%) provides an easy-to-understand representation of this proportion.
Further Mathematical Exploration: Working with Fractions
Understanding 25/230 allows us to delve deeper into fundamental mathematical concepts:
- Proportions: Fractions represent proportions, indicating the relationship between two quantities. The fraction 25/230 shows the proportion of 25 out of 230.
- Ratios: Similar to proportions, ratios compare two quantities. The ratio of people who preferred the coffee brand to those who didn't is 25:205 (which simplifies to 5:41).
- Equivalent Fractions: Different fractions can represent the same value. 25/230 and 5/46 are equivalent fractions.
- Improper Fractions and Mixed Numbers: While 25/230 is a proper fraction (numerator < denominator), understanding improper fractions (numerator ≥ denominator) and mixed numbers (a whole number and a proper fraction) is crucial for broader mathematical comprehension.
Frequently Asked Questions (FAQ)
Q1: How do I simplify a fraction like 25/230?
A1: Find the greatest common divisor (GCD) of the numerator and denominator. Divide both the numerator and the denominator by the GCD. The resulting fraction is the simplified form.
Q2: What is the decimal equivalent of 25/230?
A2: Divide the numerator (25) by the denominator (230). The result is approximately 0.1087.
Q3: How do I convert 25/230 to a percentage?
A3: Convert the fraction to a decimal (as in Q2) and then multiply by 100. The result is approximately 10.87%.
Q4: Are there any other fractions equivalent to 25/230?
A4: Yes, any fraction obtained by multiplying or dividing both the numerator and denominator by the same non-zero number will be equivalent. For example, 50/460, 75/690, etc., are all equivalent to 25/230. However, 5/46 is the simplest equivalent fraction.
Q5: What if the fraction had larger numbers? How would I simplify it?
A5: For larger numbers, the Euclidean algorithm is a more efficient method to find the GCD. You can also use prime factorization to find the GCD. Both methods are explained in detail in higher-level mathematics texts.
Conclusion: Mastering Fractions for Real-World Success
Understanding fractions is a fundamental skill with broad applications. This in-depth look at the fraction 25/230 demonstrates the processes of simplification, conversion to decimals and percentages, and real-world application. Mastering these concepts enhances your problem-solving abilities across various fields, from everyday calculations to advanced mathematical studies. Remember that the ability to work comfortably with fractions is a building block for success in many areas of life. By practicing these methods and exploring related concepts, you can build confidence and proficiency in handling fractions and related mathematical tasks. The key is to approach the subject methodically and break down the problems into manageable steps.
Latest Posts
Latest Posts
-
19 20 To Decimal
Sep 15, 2025
-
Author Sarah Knight
Sep 15, 2025
-
4 Of 80
Sep 15, 2025
-
Pg To Ng
Sep 15, 2025
-
99f In C
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 230 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.