35 - 12
interactiveleap
Sep 15, 2025 · 6 min read
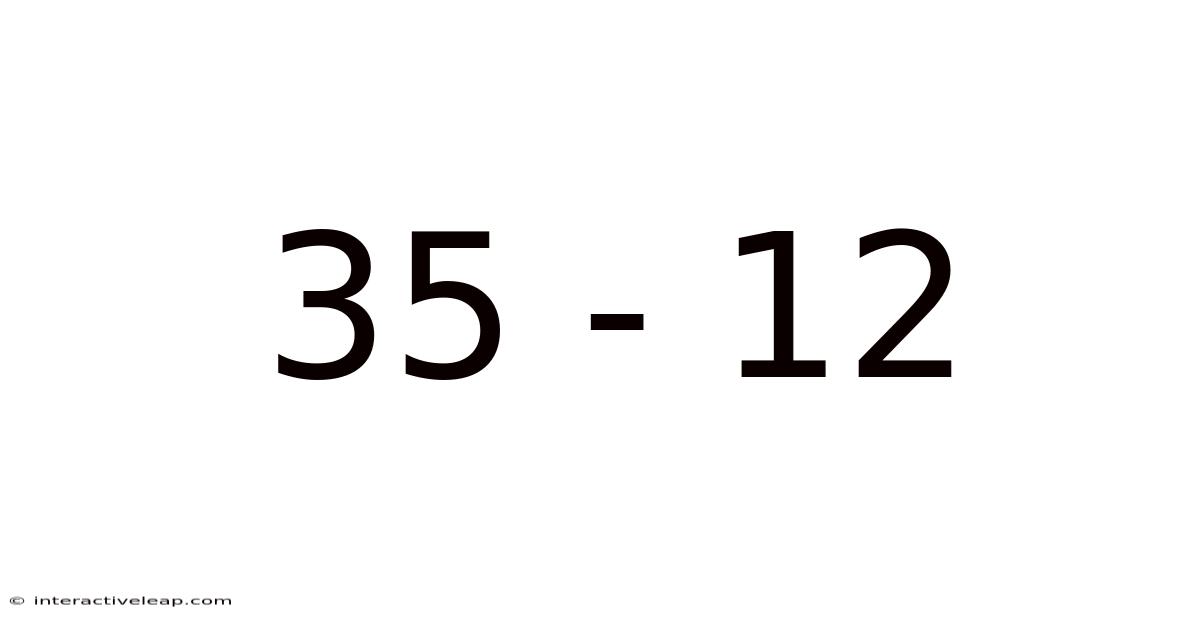
Table of Contents
Understanding Subtraction: A Deep Dive into 35 - 12
This article will explore the seemingly simple subtraction problem, 35 - 12, but delve much deeper than a simple answer. We'll examine various methods for solving this problem, the underlying mathematical concepts, and expand upon the core principles to tackle more complex subtractions. This will be a comprehensive guide suitable for learners of all levels, from elementary school students grasping the basics to those seeking a more robust understanding of arithmetic. We'll explore different approaches, including visual aids and real-world applications, making the process engaging and easy to understand.
Introduction to Subtraction
Subtraction is one of the four fundamental arithmetic operations, alongside addition, multiplication, and division. It represents the process of removing objects from a collection or finding the difference between two quantities. In its simplest form, subtraction answers the question, "What remains when a certain amount is taken away?" The problem 35 - 12 asks: "If you have 35 objects and remove 12, how many are left?"
The number 35 is called the minuend, the number being subtracted from. The number 12 is the subtrahend, the number being subtracted. The result, or answer, is called the difference.
Methods for Solving 35 - 12
Let's explore several ways to solve 35 - 12, catering to different learning styles and levels of understanding:
1. Using Concrete Objects (Manipulatives)
This is a fantastic method for younger learners. Gather 35 of any small objects – beads, buttons, blocks, etc. Count out 12 and remove them from the group. Count the remaining objects. This hands-on approach provides a concrete understanding of the subtraction process. This visual representation reinforces the concept of 'taking away'.
2. Number Line Subtraction
A number line visually represents numbers in a sequential order. Start at 35 on the number line. Then, move 12 units to the left. The point you land on represents the difference. This method helps visualize the reduction in quantity.
3. Decomposition Method (Breaking Down Numbers)
This method involves breaking down the subtrahend (12) into smaller, easier-to-manage numbers.
- Step 1: Break 12 down: 12 = 10 + 2
- Step 2: Subtract 10 from 35: 35 - 10 = 25
- Step 3: Subtract 2 from the result: 25 - 2 = 23
Therefore, 35 - 12 = 23. This method is beneficial for breaking down more complex problems into simpler steps.
4. Standard Algorithm (Borrowing/Regrouping)
This is the traditional method taught in most schools. It involves working with the ones and tens columns separately.
- Ones Column: We can't directly subtract 2 from 5 (5 - 2 = 3).
- Tens Column: We need to borrow one ten from the tens column (3 tens become 2 tens). This borrowed ten is added to the ones column, transforming the 5 into 15.
- Ones Column: Now we subtract: 15 - 2 = 13
- Tens Column: Subtract the remaining tens: 2 - 1 = 1
- Combine: The result is 13 (ones) and 1 (tens), giving us 23.
This method necessitates a solid understanding of place value (ones, tens, hundreds, etc.).
5. Using Addition (Inverse Operation)
Subtraction and addition are inverse operations. This means that they "undo" each other. To solve 35 - 12, we can ask: "What number, when added to 12, equals 35?" Thinking about addition can help solve subtraction problems. This approach builds a deeper understanding of the relationship between the two operations.
The Importance of Place Value in Subtraction
Understanding place value is crucial for accurate subtraction, especially with larger numbers. In the number 35, the 3 represents 3 tens (or 30), and the 5 represents 5 ones. The concept of place value allows us to break down numbers into their constituent parts, making subtraction more manageable. Mastering place value is essential for moving beyond simple subtraction problems.
Extending Subtraction Skills: More Complex Examples
Once comfortable with 35 - 12, we can progress to more challenging subtraction problems. The same methods discussed above – decomposition, the standard algorithm, and using the number line – can be applied.
Example 1: Three-Digit Subtraction
Let's try 157 - 84.
Using the standard algorithm:
- Ones column: 7 - 4 = 3
- Tens column: 5 - 8. We need to borrow 1 hundred (making it 15 tens). 15 - 8 = 7
- Hundreds column: 1 - 0 = 1
Therefore, 157 - 84 = 73.
Example 2: Subtraction with Zeroes
Subtracting numbers containing zeroes often presents unique challenges. For instance, consider 403 - 125:
- Ones column: 3 - 5. We need to borrow from the tens column, but there's a zero.
- Tens column: Borrow from the hundreds column (making it 3 hundreds and 10 tens). Then borrow from the tens column. This gives 9 tens and 13 ones.
- Ones column: 13 - 5 = 8
- Tens column: 9 - 2 = 7
- Hundreds column: 3 - 1 = 2
Therefore, 403 - 125 = 278
Real-World Applications of Subtraction
Subtraction is an essential life skill, appearing in numerous everyday situations:
- Shopping: Calculating the change received after a purchase.
- Cooking: Measuring ingredients according to a recipe.
- Budgeting: Tracking expenses and calculating remaining funds.
- Time Management: Determining the duration of an event (e.g., end time minus start time).
- Distance Calculations: Finding the distance remaining on a journey.
Frequently Asked Questions (FAQ)
Q: What if I get a negative number when subtracting?
A: A negative number indicates that the subtrahend is larger than the minuend. This can sometimes happen in real-world scenarios – for instance, if you spend more money than you have.
Q: Is there a limit to how large the numbers can be in subtraction?
A: No, the principles of subtraction apply to numbers of any size, from small integers to extremely large numbers. However, the calculation may become more complex and time-consuming with larger numbers.
Q: Are there other ways to check my answer after subtraction?
A: Yes, you can use addition to verify your answer. Add the difference to the subtrahend; the result should be the minuend. For example, in 35 - 12 = 23, 23 + 12 = 35.
Q: Why is understanding subtraction important?
A: Subtraction is foundational to higher-level mathematics. A strong understanding of subtraction is essential for mastering algebra, calculus, and many other mathematical concepts. It also equips individuals with valuable problem-solving skills applicable to everyday life.
Conclusion
Subtraction, while seemingly straightforward, is a fundamental mathematical concept with broad applications. By exploring different methods and understanding the underlying principles of place value, individuals can build a strong foundation in arithmetic and tackle more complex problems with confidence. From manipulating objects to utilizing the standard algorithm, the approach should be tailored to suit individual learning styles. Remember to practice regularly to improve speed and accuracy. The mastery of subtraction paves the way for success in higher-level mathematics and strengthens critical thinking abilities.
Latest Posts
Latest Posts
-
70 Of 180
Sep 15, 2025
-
19 20 To Decimal
Sep 15, 2025
-
Author Sarah Knight
Sep 15, 2025
-
4 Of 80
Sep 15, 2025
-
Pg To Ng
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 35 - 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.