2/9 X 45
interactiveleap
Sep 21, 2025 · 6 min read
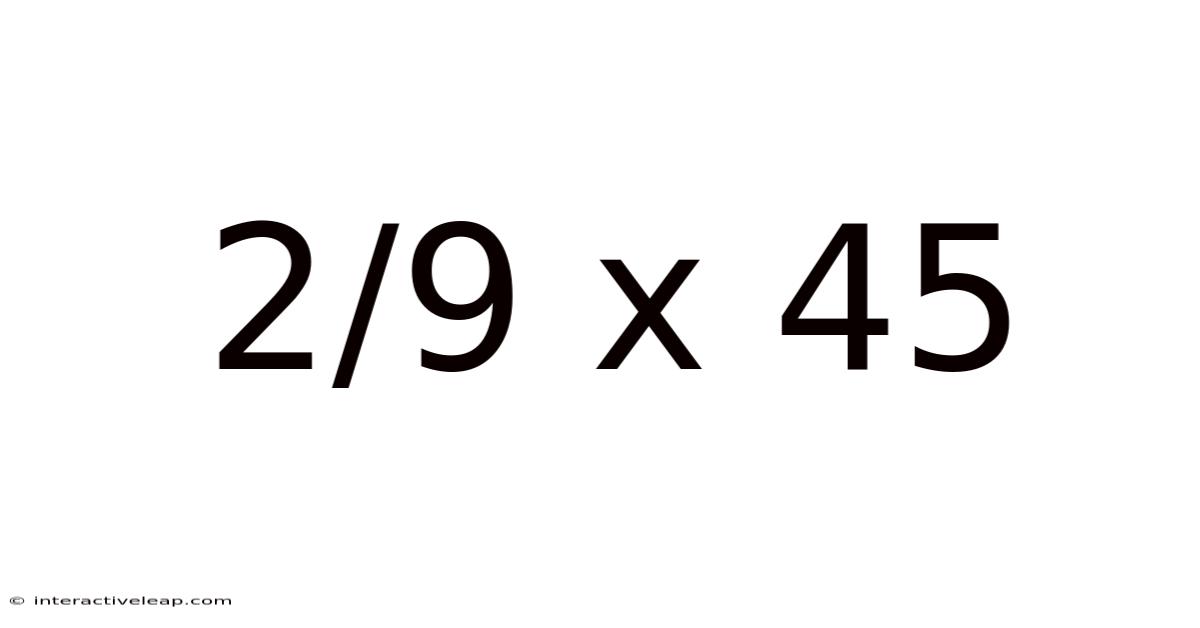
Table of Contents
Decoding 2/9 x 45: A Deep Dive into Fraction Multiplication
This article explores the seemingly simple calculation of 2/9 x 45, but goes far beyond a mere answer. We'll unravel the underlying principles of fraction multiplication, delve into different solution methods, and explore the broader mathematical concepts involved. This comprehensive guide is perfect for students struggling with fractions, those looking to refresh their math skills, and anyone curious about the elegance of mathematical operations. We'll cover everything from the basics of fractions to advanced simplification techniques, ensuring a complete understanding of this fundamental arithmetic operation.
Understanding Fractions: A Quick Recap
Before tackling 2/9 x 45, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 2/9, the denominator 9 means the whole is divided into 9 equal parts, and the numerator 2 indicates we are considering 2 of those parts.
Method 1: Direct Multiplication
The most straightforward method to solve 2/9 x 45 is to perform direct multiplication. Remember that a whole number can be expressed as a fraction with a denominator of 1. Therefore, we can rewrite 45 as 45/1. Our equation now becomes:
(2/9) x (45/1)
In fraction multiplication, we multiply the numerators together and the denominators together:
(2 x 45) / (9 x 1) = 90 / 9
Now, we simplify the resulting fraction by dividing the numerator and denominator by their greatest common divisor (GCD), which is 9:
90 ÷ 9 / 9 ÷ 9 = 10/1 = 10
Therefore, 2/9 x 45 = 10
Method 2: Simplification Before Multiplication
A more efficient approach involves simplifying the fraction before performing the multiplication. This method reduces the size of the numbers involved, making the calculation easier and reducing the risk of errors. Observe that 45 and 9 share a common factor, which is 9. We can simplify the expression as follows:
(2/9) x (45/1) = (2/1) x (5/1) (Since 45/9 simplifies to 5)
Now, multiply the numerators and denominators:
(2 x 5) / (1 x 1) = 10/1 = 10
This method achieves the same result with fewer steps, demonstrating the power of simplifying fractions before carrying out the multiplication.
Method 3: Converting the Fraction to a Decimal
Another way to solve this problem involves converting the fraction 2/9 into a decimal. To do this, divide the numerator (2) by the denominator (9):
2 ÷ 9 ≈ 0.222... (This is a recurring decimal)
Now, multiply this decimal by 45:
0.222... x 45 ≈ 10
While this method yields the correct answer, it's important to note the inherent limitations of using recurring decimals. Rounding errors can occur, leading to slight inaccuracies depending on the level of precision used. Therefore, the fraction method remains the most accurate approach.
The Importance of Understanding the Process
While obtaining the answer (10) is crucial, understanding the how is equally, if not more important. This process showcases fundamental mathematical concepts:
-
Fraction Multiplication: The core concept lies in understanding how to multiply fractions. The method of multiplying numerators and denominators separately is fundamental to numerous mathematical operations.
-
Simplification of Fractions: Simplifying fractions before multiplication streamlines the calculation, making it more efficient and reducing potential errors. This skill is essential for efficient problem-solving.
-
Greatest Common Divisor (GCD): Finding the GCD helps in simplifying fractions to their lowest terms. Understanding how to find the GCD is a key element of number theory and essential for simplifying complex mathematical expressions.
-
Equivalent Fractions: The simplification process also demonstrates the concept of equivalent fractions. Fractions like 90/9 and 10/1 represent the same value, but 10/1 is the simplified form.
Expanding the Concept: Applications of Fraction Multiplication
The simple calculation of 2/9 x 45 might seem isolated, but its principles have widespread applications in various fields:
-
Everyday Life: Imagine calculating discounts (2/9 off a $45 item), splitting bills among friends, or measuring ingredients for a recipe. Fraction multiplication is used frequently in these daily scenarios.
-
Science: In scientific experiments and data analysis, fractions are used to represent proportions and ratios. Multiplying fractions is vital for manipulating and analyzing this data.
-
Engineering: Engineering designs and calculations often involve fractional measurements and proportions. Accurate fraction multiplication is critical for precision and safety.
-
Finance: Understanding fractional percentages and calculating interest rates requires a solid understanding of fraction multiplication.
-
Computer Science: In computer graphics and algorithms, fractions are used to represent coordinates and proportions, making fraction multiplication a critical aspect of programming.
Frequently Asked Questions (FAQ)
Q: Can I solve this problem using a calculator?
A: Yes, most calculators can handle fraction multiplication. However, it's beneficial to understand the underlying principles before relying solely on a calculator. Understanding the manual process strengthens your mathematical foundation.
Q: What if the fraction was 2/9 x 46 instead of 45?
A: The process remains the same. You would still multiply the numerators and denominators and then simplify the resulting fraction. In this case, there is no common factor between 46 and 9, so the simplification step would be slightly different, resulting in a fractional answer, not a whole number.
Q: Are there other methods to solve this type of problem?
A: While the methods outlined above are the most common and efficient, more advanced techniques exist for handling more complex fraction multiplication problems, especially those involving algebraic expressions.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes the numbers smaller and easier to manage, reducing the risk of errors, and producing a more concise and understandable answer. It helps in visualizing the proportion effectively.
Conclusion
The seemingly simple problem of 2/9 x 45 provides a powerful gateway to understanding fundamental mathematical concepts related to fractions. From the basic mechanics of fraction multiplication to the importance of simplification and the diverse applications in various fields, this calculation offers a valuable lesson in mathematical proficiency. Mastering fraction multiplication is not just about getting the right answer (which is 10); it's about understanding the underlying principles and appreciating the elegance and practicality of this essential mathematical operation. By grasping these concepts, you'll build a stronger foundation for tackling more complex mathematical challenges in the future. Remember to practice regularly, explore different problem-solving approaches, and never underestimate the power of understanding the "why" behind the "how."
Latest Posts
Latest Posts
-
45 12
Sep 21, 2025
-
Knockback Stick Command
Sep 21, 2025
-
The Number Devil
Sep 21, 2025
-
72 X 3
Sep 21, 2025
-
Bubble Level Up
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2/9 X 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.