45 / 12
interactiveleap
Sep 21, 2025 · 6 min read
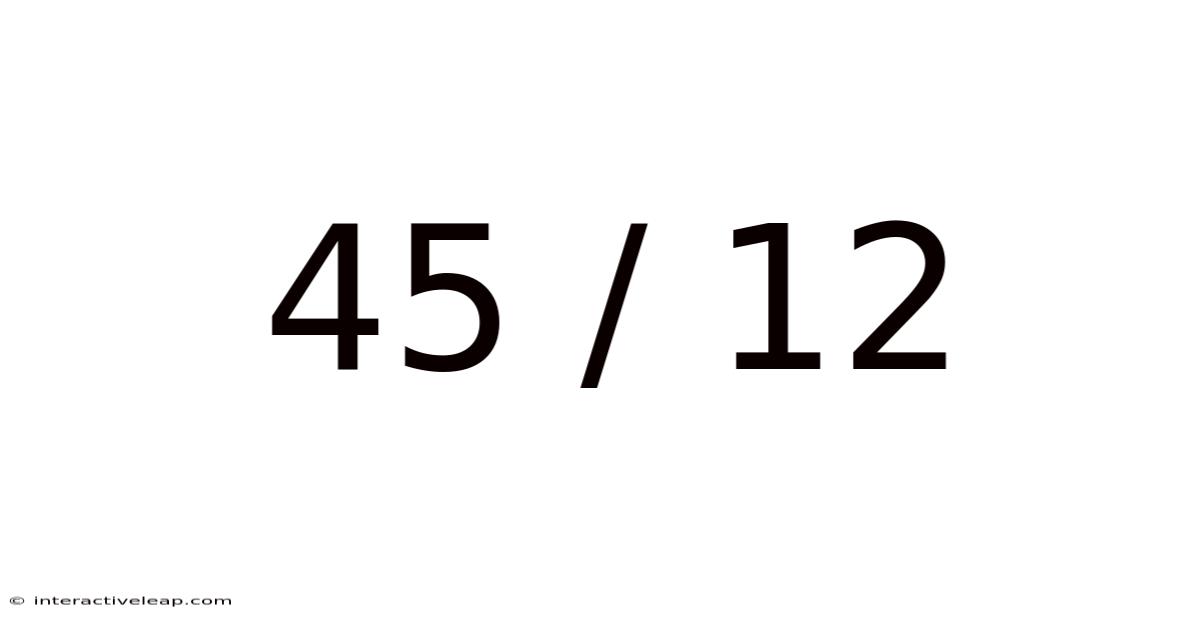
Table of Contents
Unveiling the Mystery of 45/12: A Deep Dive into Division, Fractions, and Decimals
The seemingly simple division problem, 45/12, opens a door to a fascinating world of mathematical concepts. It’s more than just finding a quotient; it’s an opportunity to explore fractions, decimals, mixed numbers, and the fundamental principles of division. This comprehensive guide will delve into the various methods of solving 45/12, explaining the underlying mathematical principles and offering practical applications. Understanding 45/12 isn't just about getting the right answer; it's about grasping the interconnectedness of mathematical ideas.
Understanding the Problem: 45/12
At its core, 45/12 represents the division of 45 into 12 equal parts. This can be interpreted in several real-world scenarios: dividing 45 cookies equally among 12 friends, splitting a 45-minute workout into 12 equal intervals, or calculating the average score from 12 tests totaling 45 points. The solution will reveal how many whole units are in each part and the remaining fraction or decimal portion.
Method 1: Long Division
The most traditional approach to solving 45/12 is through long division. This method breaks down the division into manageable steps:
-
Set up the problem: Write 45 inside the long division symbol (÷) and 12 outside.
-
Divide: How many times does 12 go into 45? It goes in 3 times (3 x 12 = 36). Write the 3 above the 5 in 45.
-
Multiply: Multiply the quotient (3) by the divisor (12): 3 x 12 = 36.
-
Subtract: Subtract the result (36) from the dividend (45): 45 - 36 = 9.
-
Bring down: Since there are no more digits to bring down, the 9 represents the remainder.
Therefore, using long division, 45/12 = 3 with a remainder of 9. This can be written as 3 R 9.
Method 2: Fractions and Simplification
We can also represent 45/12 as a fraction. This allows us to explore further simplification:
-
Find the Greatest Common Divisor (GCD): The GCD of 45 and 12 is 3. This means both numbers can be divided evenly by 3.
-
Simplify the fraction: Divide both the numerator (45) and the denominator (12) by the GCD (3):
45 ÷ 3 = 15 12 ÷ 3 = 4
This simplifies the fraction to 15/4.
This fraction, 15/4, represents the exact answer. It shows that 45 divided by 12 equals 15 fourths.
Method 3: Mixed Numbers
A mixed number combines a whole number and a fraction. It's a convenient way to represent the result of 45/12:
-
Convert the improper fraction: The fraction 15/4 is an improper fraction because the numerator (15) is larger than the denominator (4).
-
Divide the numerator by the denominator: 15 ÷ 4 = 3 with a remainder of 3.
-
Express as a mixed number: The quotient (3) becomes the whole number, and the remainder (3) becomes the numerator of a fraction with the original denominator (4). Therefore, 15/4 is equivalent to 3 3/4.
This means 45/12 is equal to 3 and 3/4. This is a more intuitive representation than the improper fraction or the remainder notation.
Method 4: Decimals
Converting 45/12 to a decimal involves long division, but it continues beyond the remainder stage:
-
Perform long division: As before, long division gives us 3 with a remainder of 9.
-
Add a decimal point and zeros: Add a decimal point to the dividend (45) and add zeros after it. This allows us to continue the division.
-
Continue the division: Divide 90 by 12, which equals 7.5.
Therefore, 45/12 = 3.75 as a decimal.
Illustrative Examples: Real-World Applications
The solution to 45/12 finds practical application in various contexts:
-
Baking: If a recipe calls for 45 grams of flour and you need to divide it into 12 equal portions for mini-cakes, each portion would require 3.75 grams of flour.
-
Time Management: Dividing a 45-minute workout into 12 equal intervals results in 3.75-minute segments for focused exercises.
-
Finance: If 12 equal monthly payments total $45, each payment would amount to $3.75.
-
Average Calculation: If 12 quizzes have a combined score of 45 points, the average score per quiz is 3.75 points.
Mathematical Principles at Play
Solving 45/12 reinforces several crucial mathematical principles:
-
Division: The fundamental operation of dividing a quantity into equal parts.
-
Fractions: Representing parts of a whole, illustrating the relationship between the numerator and denominator.
-
Improper Fractions: Fractions where the numerator is greater than or equal to the denominator.
-
Mixed Numbers: Combining whole numbers and fractions for a more intuitive representation.
-
Decimals: Expressing numbers as fractions with denominators that are powers of 10.
-
Greatest Common Divisor (GCD): Finding the largest number that divides evenly into two or more numbers, facilitating fraction simplification.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 45/12?
A: The simplest form is 15/4 or 3 3/4. This is achieved by finding the greatest common divisor (GCD) of 45 and 12, which is 3, and dividing both the numerator and denominator by 3.
Q: Can I use a calculator to solve 45/12?
A: Yes, a calculator will directly provide the decimal answer, 3.75. However, understanding the different methods of solving this problem offers a deeper understanding of the underlying mathematical concepts.
Q: Why is it important to learn different methods for solving 45/12?
A: Learning multiple methods provides a more comprehensive understanding of fractions, decimals, and division. It also helps develop problem-solving skills and adaptability in tackling different mathematical situations.
Q: What if the remainder in long division is not zero?
A: A non-zero remainder indicates that the division is not exact. The remainder can be expressed as a fraction (by placing the remainder over the divisor) or included in the decimal representation.
Q: How do I choose the best method to solve a division problem?
A: The best method depends on the context and the required form of the answer. If an exact fraction is needed, simplifying fractions is the preferred method. If a decimal is required, long division with decimal expansion is suitable. Mixed numbers offer a more intuitive representation in many situations.
Conclusion
Solving 45/12 is more than a simple arithmetic exercise; it’s a gateway to understanding fundamental mathematical principles. This exploration has illustrated multiple methods—long division, fraction simplification, mixed numbers, and decimals—each offering a unique perspective on the problem. By mastering these methods, you’re not only finding the answer (3.75 or 3 3/4) but also strengthening your foundational mathematical skills, enhancing your problem-solving abilities, and appreciating the interconnectedness of different mathematical concepts. The ability to approach a problem like 45/12 from various angles fosters mathematical fluency and confidence. Remember, the journey of understanding is often more valuable than just the destination.
Latest Posts
Latest Posts
-
L O F
Sep 21, 2025
-
20 Off 34
Sep 21, 2025
-
92inches In Cm
Sep 21, 2025
-
Keystroke Per Hour
Sep 21, 2025
-
90 Of 150
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 45 / 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.