19.2 X Pi
interactiveleap
Sep 20, 2025 · 5 min read
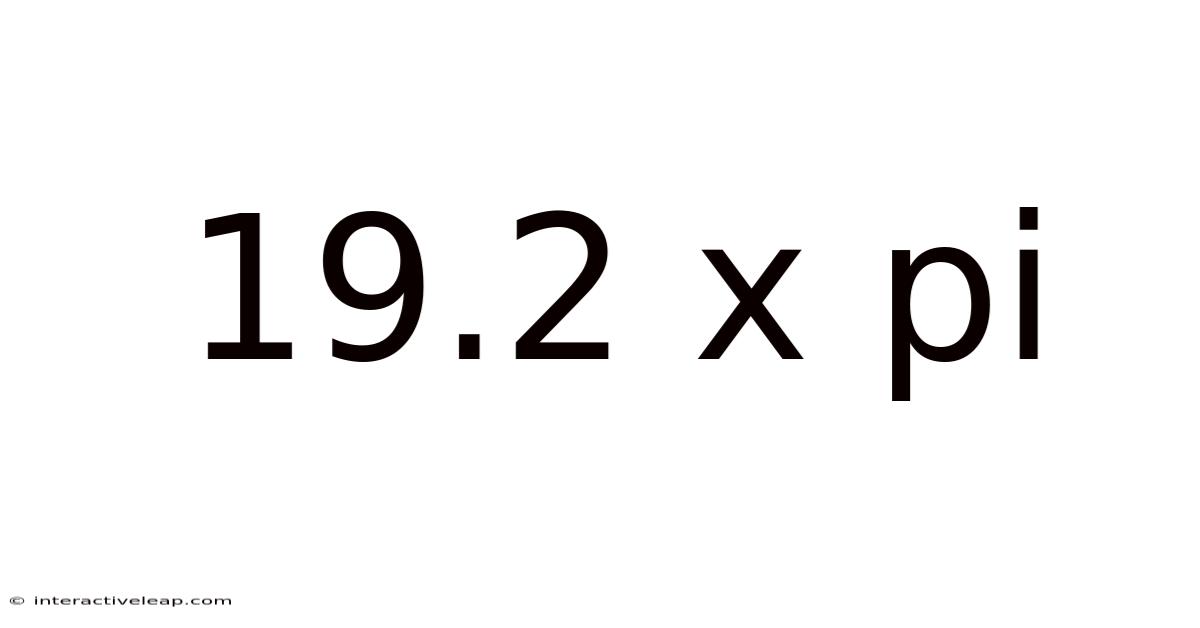
Table of Contents
Unraveling the Mystery of 19.2 x π: A Deep Dive into Circumference, Area, and Beyond
The seemingly simple expression "19.2 x π" hides a wealth of mathematical concepts and real-world applications. At first glance, it's just a multiplication problem, but understanding its implications reveals fundamental principles of geometry, particularly concerning circles and their properties. This article will explore the significance of this calculation, delving into its practical uses, the underlying mathematical theory, and addressing common questions surrounding it. We'll journey from basic circumference calculations to more advanced applications, ensuring a comprehensive understanding suitable for all levels of mathematical comprehension.
Understanding the Fundamentals: π and its Significance
Before we delve into the specifics of 19.2 x π, let's establish a solid foundation. The Greek letter π (pi) represents the ratio of a circle's circumference to its diameter. This ratio is a constant, approximately equal to 3.14159, and is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. This seemingly simple constant is crucial in numerous mathematical and scientific fields.
The value of π is crucial for calculating various properties of circles, including:
- Circumference: The distance around the circle, calculated as C = πd or C = 2πr, where 'd' is the diameter and 'r' is the radius.
- Area: The space enclosed within the circle, calculated as A = πr².
- Volume and Surface Area of Spheres and Cylinders: π plays a central role in calculating the volume and surface area of three-dimensional shapes derived from circles.
19.2 x π: A Circumference Calculation
In the context of "19.2 x π", the number 19.2 most likely represents the diameter of a circle. Therefore, 19.2 x π directly calculates the circumference of that circle. By multiplying the diameter by π, we obtain the total distance around the circle. Using a calculator, we find that 19.2 x π ≈ 60.3185789489.
Let's round this to a more practical value, depending on the context. For many applications, 60.32 units (where the units could be centimeters, meters, inches, etc.) would be sufficiently accurate. However, for applications requiring higher precision, more decimal places would be necessary. The precision needed depends entirely on the application.
This simple calculation has wide-ranging practical applications. Consider these examples:
- Engineering: Calculating the circumference of a circular component is essential in various engineering disciplines, such as designing pipes, gears, or wheels. Accuracy is paramount in these situations.
- Construction: When building circular structures, accurately determining the circumference is crucial for material estimation and proper construction.
- Manufacturing: In manufacturing processes involving circular objects, precise measurements are vital for quality control and efficiency.
- Cartography: Calculating the circumference of the Earth (or a portion of it) plays a vital role in mapping and geographic information systems (GIS).
Beyond Circumference: Exploring Other Applications
While calculating the circumference is the most immediate application of 19.2 x π, it opens doors to further calculations and understanding. For example, knowing the circumference allows us to calculate the radius and subsequently the area of the circle.
If we know the circumference (approximately 60.32 units), we can calculate the radius using the formula:
r = C / (2π) ≈ 60.32 / (2π) ≈ 9.6 units
Then, we can use the radius to calculate the area:
A = πr² ≈ π(9.6)² ≈ 289.5 square units.
Extending the Concept: Three-Dimensional Applications
The principles extend beyond two-dimensional circles. If we consider a cylinder with a diameter of 19.2 units and a specific height, we can use 19.2 x π to calculate the circumference of its base. This is crucial for determining the surface area and volume of the cylinder. Similarly, if we consider a sphere with a diameter of 19.2 units, we can use related calculations involving π to determine its surface area and volume.
The formula for the surface area of a sphere is 4πr², and the formula for the volume is (4/3)πr³. These formulas demonstrate the pervasive role of π in calculations involving three-dimensional shapes.
The Mathematical Precision of π
It's important to remember that π is an irrational number. This means its decimal representation is non-terminating and non-repeating. Calculators provide approximations, and the level of precision depends on the calculator's capabilities. For most practical purposes, using a value of π accurate to several decimal places (e.g., 3.14159) is sufficient. However, in highly precise calculations or scientific applications, more significant figures might be necessary.
Addressing Frequently Asked Questions (FAQs)
Q1: What is the exact value of 19.2 x π?
A1: There is no exact decimal representation of 19.2 x π because π is an irrational number. Any value calculated will be an approximation.
Q2: Why is π so important in mathematics?
A2: π is fundamental because it describes a fundamental relationship between a circle's diameter and its circumference. This relationship appears in countless geometric and scientific contexts.
Q3: Are there other ways to calculate the circumference besides using π?
A3: While π is the most common and efficient method, other techniques exist, but they are less direct and often less practical. Approximations using polygons inscribed within a circle could be used, but these methods are less precise and more computationally intensive.
Q4: What are the units of measurement for 19.2 x π?
A4: The units depend on the units of the diameter (19.2). If the diameter is measured in centimeters, then the circumference will be in centimeters. Similarly, if the diameter is in meters, inches, or any other unit of length, the circumference will have the same unit.
Conclusion: The Enduring Importance of 19.2 x π
The seemingly simple calculation 19.2 x π encapsulates fundamental mathematical principles and has broad applications in various fields. Understanding the role of π in calculating the circumference, area, and volumes of circles and related shapes is crucial for anyone pursuing studies or careers in science, engineering, mathematics, or any field requiring precise measurements and geometric understanding. By grasping the essence of this calculation, we not only solve a mathematical problem but also gain a deeper appreciation for the elegant and fundamental nature of mathematics. The seemingly simple expression opens a door to a wider world of mathematical understanding and practical applications. Remember that while we often use approximations for π, the underlying mathematical principles remain consistent and incredibly powerful.
Latest Posts
Latest Posts
-
Horizontal Progressive Evacuation
Sep 20, 2025
-
25 Of 225
Sep 20, 2025
-
1 9 X 1 9
Sep 20, 2025
-
Micron Mm Conversion
Sep 20, 2025
-
5 8 Of 720
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 19.2 X Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.