1/9 X 1/9
interactiveleap
Sep 20, 2025 · 5 min read
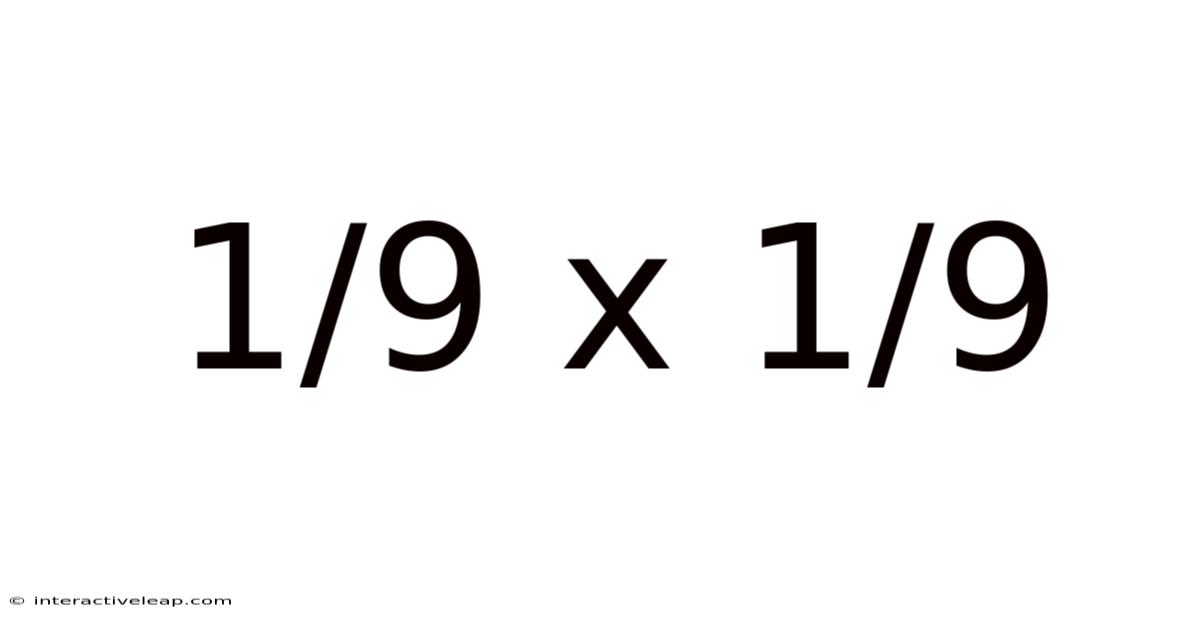
Table of Contents
Unraveling the Mystery of 1/9 x 1/9: A Deep Dive into Fraction Multiplication
Have you ever encountered a simple math problem that unexpectedly sparked a deeper understanding of fundamental concepts? The seemingly straightforward calculation of 1/9 x 1/9 often serves as just such a problem. While the answer might seem immediately obvious to some, exploring this calculation offers a fantastic opportunity to delve into the intricacies of fraction multiplication, solidify our understanding of fractions, and even touch upon related mathematical concepts. This comprehensive guide will walk you through the process step-by-step, exploring the underlying principles and broadening your mathematical horizons.
Understanding Fractions: A Refresher
Before tackling the multiplication itself, let's ensure we have a solid grasp of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/9, the numerator (1) represents one part, and the denominator (9) represents that the whole is divided into nine equal parts.
Multiplying Fractions: The Simple Rule
The beauty of fraction multiplication lies in its simplicity. To multiply two fractions, we follow this straightforward rule:
Multiply the numerators together, and then multiply the denominators together.
This simple process gives us the result of multiplying the two fractions. Let's apply this rule to our problem: 1/9 x 1/9.
Calculating 1/9 x 1/9: A Step-by-Step Approach
-
Multiply the Numerators: 1 x 1 = 1
-
Multiply the Denominators: 9 x 9 = 81
-
Combine the Results: Therefore, 1/9 x 1/9 = 1/81
So, the answer to our initial problem is 1/81. But our exploration doesn't end here. Let's delve deeper into the meaning and implications of this result.
Visualizing Fraction Multiplication: A Geometrical Approach
Imagine a square divided into nine equal parts, representing the fraction 1/9. Now, imagine taking one of those nine parts (1/9) and further dividing that part into nine equal pieces. This visual representation perfectly illustrates the result of 1/9 x 1/9. Each of the smaller squares now represents 1/81 of the original whole square. This visual approach is particularly helpful for understanding the concept of fraction multiplication, especially for those who benefit from visual aids.
Connecting to Decimal Representation: From Fractions to Decimals
While fractions are a precise way to represent parts of a whole, decimal representation provides an alternative viewpoint. Let's convert our fractions into decimals:
- 1/9 ≈ 0.1111 (repeating)
- 1/81 ≈ 0.0123456790123… (repeating)
Note that both 1/9 and 1/81 yield repeating decimals. The repeating nature of these decimals underscores the inherent properties of fractions and their relationship to the decimal system.
Exploring Related Concepts: Powers and Exponents
Our problem, 1/9 x 1/9, can also be expressed using exponents: (1/9)² . This introduces the concept of raising a fraction to a power. In this case, we are squaring the fraction 1/9, which means multiplying it by itself. This shows the connection between fraction multiplication and the broader concept of exponents and powers, laying the groundwork for more advanced mathematical explorations.
Extending the Concept: Multiplying More Than Two Fractions
The principles of fraction multiplication extend seamlessly to multiplying three or more fractions. We simply continue multiplying numerators together and denominators together. For instance, 1/9 x 1/9 x 1/9 = 1/729. This showcases the scalability of the fundamental rule and solidifies our understanding of its consistent application.
Dealing with Mixed Numbers: A Practical Application
While our example focused on simple fractions, let's consider an application with mixed numbers. A mixed number consists of a whole number and a fraction (e.g., 2 1/2). To multiply fractions involving mixed numbers, we first convert the mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to the denominator. Then, we follow the standard multiplication rule. This illustrates the adaptability of the method to more complex scenarios, highlighting its versatility and practical use.
Simplifying Fractions: A Crucial Step
Once we have the result of multiplying fractions, it's often beneficial to simplify the resulting fraction to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. In the case of 1/81, the fraction is already in its simplest form because 1 and 81 share no common divisors other than 1. However, understanding fraction simplification is crucial for many other multiplication problems.
Real-World Applications: Where Do Fractions Matter?
Fractions are not just abstract mathematical concepts; they have numerous practical applications in everyday life. From cooking and baking (measuring ingredients) to calculating proportions in construction and engineering, fractions are an integral part of our world. Understanding fraction multiplication empowers us to tackle these real-world problems effectively and confidently.
Frequently Asked Questions (FAQ)
Q1: What happens if I multiply a fraction by 1?
A1: Multiplying any fraction by 1 does not change the value of the fraction. This is because 1 is the multiplicative identity.
Q2: Can I multiply fractions with different denominators?
A2: Absolutely! The rule for multiplying fractions applies regardless of whether the denominators are the same or different.
Q3: What if the numerator is larger than the denominator?
A3: This is an improper fraction. You can multiply it just like any other fraction, but it is often helpful to convert it to a mixed number for easier interpretation.
Q4: Why is simplifying fractions important?
A4: Simplifying fractions presents the result in the clearest and most concise form. It simplifies further calculations and makes the result easier to understand.
Conclusion: Beyond the Basics
While the initial calculation of 1/9 x 1/9 might seem trivial, our exploration has unveiled a wealth of related concepts and applications. We've journeyed from the fundamentals of fraction multiplication to the visualization of fractions, decimal representation, and the use of exponents. We’ve also touched upon the practical applications of fractions in the real world. This deep dive demonstrates how a seemingly simple problem can serve as a gateway to a much broader and richer understanding of mathematical principles. Remember, the journey of learning is continuous, and every problem, no matter how simple it might seem, offers an opportunity for growth and deeper understanding.
Latest Posts
Latest Posts
-
5 Of 700
Sep 20, 2025
-
30 Of 420
Sep 20, 2025
-
Aut Cursed Orb
Sep 20, 2025
-
50 Off 40
Sep 20, 2025
-
70 Of 210
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1/9 X 1/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.