15 Of 460
interactiveleap
Sep 15, 2025 · 5 min read
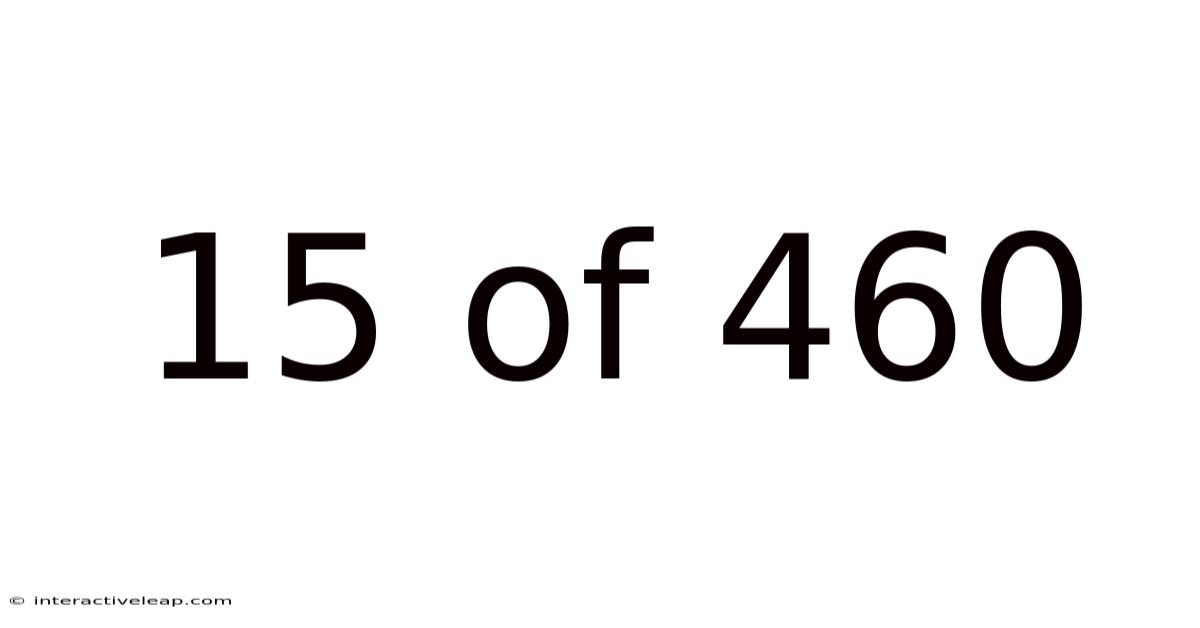
Table of Contents
Unveiling the Mystery: 15 out of 460 – Understanding Fractions, Ratios, and Percentages
The seemingly simple expression "15 out of 460" might appear insignificant at first glance. However, this seemingly small fraction holds significant implications across various fields, from statistical analysis to everyday life calculations. Understanding how to interpret and manipulate this ratio is crucial for developing strong numerical literacy. This article delves into the meaning of "15 out of 460," exploring its representation as a fraction, decimal, percentage, and its applications in real-world scenarios. We'll also unpack the underlying mathematical concepts to build a comprehensive understanding.
Introduction: Deconstructing "15 out of 460"
The phrase "15 out of 460" inherently represents a ratio. A ratio compares two quantities, indicating how much of one quantity exists relative to another. In this case, we are comparing 15 to 460. This ratio can be expressed in several equivalent forms, each offering unique advantages depending on the context. We will explore these different representations, including the fraction form (15/460), the decimal form, and the percentage form. Understanding these different representations is key to applying this ratio effectively in various problem-solving situations.
Representing 15 out of 460 as a Fraction
The most straightforward representation of "15 out of 460" is as a fraction: 15/460. This fraction indicates that 15 is a part of a larger whole, which is 460. However, fractions are often simplified to their lowest terms for easier interpretation and comparison. To simplify 15/460, we need to find the greatest common divisor (GCD) of both 15 and 460. The GCD of 15 and 460 is 5. Dividing both the numerator (15) and the denominator (460) by 5, we obtain the simplified fraction 3/92. This means that 15 out of 460 is equivalent to 3 out of 92.
Converting the Fraction to a Decimal
To convert the simplified fraction 3/92 into a decimal, we perform the division: 3 ÷ 92. This results in an approximate decimal value of 0.0326. This decimal representation provides a different perspective on the ratio, showing the proportional value of 15 relative to 460. The decimal form is useful for calculations and comparisons, particularly when dealing with other decimal values.
Expressing the Ratio as a Percentage
Percentages are a common way to express proportions, particularly in contexts requiring easy understanding and comparison. To convert the fraction 3/92 or the decimal 0.0326 into a percentage, we multiply by 100%.
(3/92) * 100% ≈ 3.26%
This indicates that 15 out of 460 represents approximately 3.26%. This percentage form is very intuitive and easily understood by a wide audience, making it a valuable tool for communication and data presentation.
Real-World Applications of the Ratio 15/460 (or 3/92)
The ratio 15 out of 460, or its simplified form 3 out of 92, has numerous applications across diverse fields. Consider these examples:
-
Statistical Analysis: Imagine a survey of 460 people, where 15 responded positively to a particular question. The ratio 15/460 (or 3.26%) would represent the proportion of positive responses. This data could be used to draw conclusions about the overall population's opinion.
-
Quality Control: In a manufacturing process, if 15 out of 460 products are defective, the 3.26% defect rate can help identify potential issues in the production line and improve quality control measures.
-
Financial Analysis: If 15 out of 460 investments yielded a profit, the ratio could be used to assess the success rate of a particular investment strategy.
-
Medical Research: In clinical trials, if 15 out of 460 participants experienced a particular side effect, the ratio helps to quantify the prevalence of that side effect.
Understanding the Mathematical Concepts
To fully grasp the implications of "15 out of 460," a strong understanding of fundamental mathematical concepts is essential. These include:
-
Fractions: Fractions represent parts of a whole. The numerator (top number) represents the part, and the denominator (bottom number) represents the whole.
-
Ratios: Ratios compare two quantities. They can be expressed as fractions, decimals, or percentages.
-
Proportions: Proportions establish an equivalence between two ratios. For example, 15/460 = 3/92 is a proportion.
-
Percentages: Percentages express a ratio as a fraction of 100. They are widely used to represent proportions in various contexts.
-
Greatest Common Divisor (GCD): The GCD is the largest number that divides two or more integers without leaving a remainder. Finding the GCD is crucial for simplifying fractions.
Expanding Understanding: Working with Proportions
Understanding proportions is crucial when working with ratios. A proportion is a statement that two ratios are equal. For instance:
15/460 = x/1000
To solve for x, we can cross-multiply:
15 * 1000 = 460 * x
15000 = 460x
x = 15000/460 ≈ 32.6
This means that if there were 1000 items, approximately 32.6 would be represented by the same ratio as 15 out of 460. This type of proportional reasoning is incredibly useful for scaling up or down ratios to fit different contexts.
Beyond the Basics: Applications in Advanced Mathematics
The seemingly simple concept of "15 out of 460" has far-reaching implications in more advanced mathematical fields. For example:
-
Probability and Statistics: This ratio could represent the probability of a particular event occurring. Statistical analysis relies heavily on understanding and manipulating proportions and probabilities.
-
Calculus: Understanding ratios and proportions is fundamental to understanding concepts like rates of change, which are central to calculus.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 15/460?
A: The simplest form is 3/92.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100%.
Q: What are some real-world examples where this type of ratio is used?
A: This ratio is used in many areas including quality control, statistical analysis, financial analysis, and medical research.
Conclusion: Mastering the Fundamentals
Understanding the meaning and implications of "15 out of 460" extends far beyond simply calculating a fraction or a percentage. It demonstrates a fundamental understanding of ratios, proportions, and their applications in various fields. By mastering these concepts, you equip yourself with valuable tools for problem-solving, critical thinking, and interpreting data effectively. The ability to express this ratio in different forms (fraction, decimal, percentage) enhances your analytical skills and empowers you to confidently tackle numerical challenges in your personal and professional life. Remember, the key is not just to calculate the answer but to understand the underlying mathematical principles and their real-world significance.
Latest Posts
Latest Posts
-
82f In C
Sep 15, 2025
-
33 X 5
Sep 15, 2025
-
33 X 4
Sep 15, 2025
-
120ml To Oz
Sep 15, 2025
-
0 4 X 4
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 460 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.