0.4 X 4
interactiveleap
Sep 15, 2025 · 5 min read
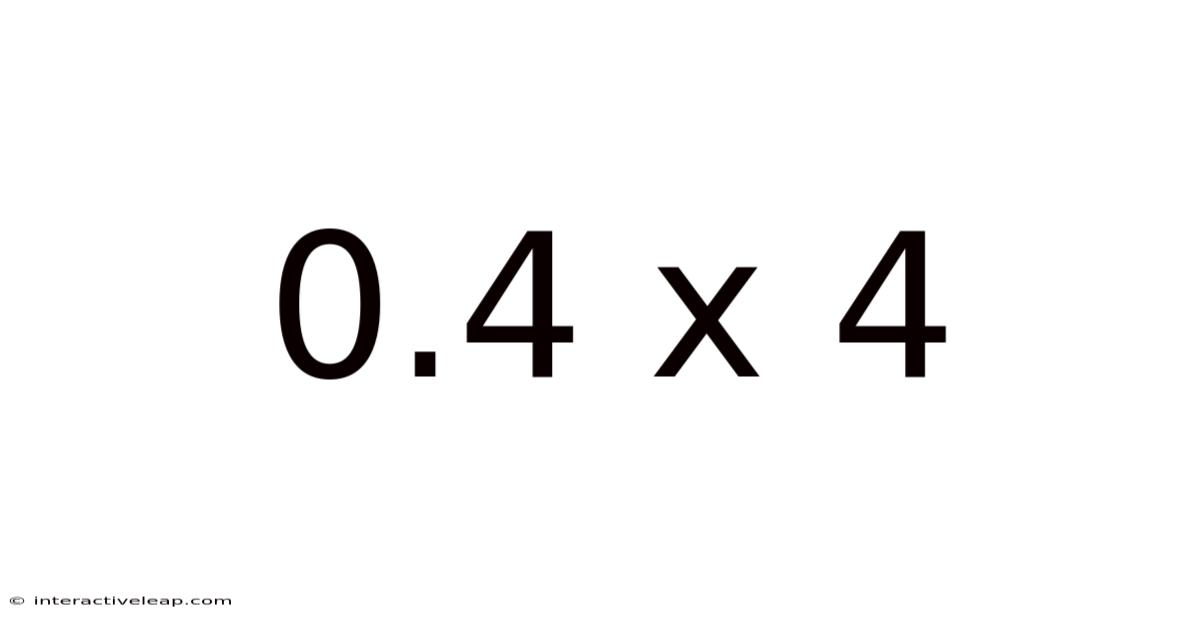
Table of Contents
Unveiling the Power of 0.4 x 4: A Deep Dive into Decimal Multiplication and its Applications
This article delves into the seemingly simple calculation of 0.4 x 4, exploring its mathematical basis, practical applications, and broader implications within the realm of decimal arithmetic. We'll move beyond the simple answer to uncover the underlying principles and demonstrate how understanding this seemingly basic calculation can unlock a deeper understanding of more complex mathematical concepts. This exploration is valuable for students of all levels, from elementary school learners grasping decimal multiplication to those seeking a refresher on fundamental mathematical operations.
Understanding Decimal Numbers
Before tackling 0.4 x 4, let's solidify our understanding of decimal numbers. Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, and so on). The decimal point separates the whole number part from the fractional part. In 0.4, the '0' represents the whole number part (zero whole units), and the '.4' represents four-tenths (4/10). Understanding this fractional representation is key to grasping decimal multiplication.
Calculating 0.4 x 4: Methods and Approaches
There are several ways to calculate 0.4 x 4, each offering a unique insight into the underlying mathematical processes:
1. Direct Multiplication:
The most straightforward method is to perform the multiplication as if the decimal point wasn't there:
4 x 4 = 16
Now, we account for the decimal point. Since 0.4 has one decimal place, we move the decimal point in the answer one place to the left:
16 becomes 1.6
Therefore, 0.4 x 4 = 1.6
2. Fractional Representation:
We can convert 0.4 into its fractional equivalent:
0.4 = 4/10
Now, the multiplication becomes:
(4/10) x 4 = 16/10
Simplifying the fraction:
16/10 = 8/5 = 1 3/5 or 1.6
This method clearly illustrates the relationship between decimals and fractions.
3. Distributive Property:
The distributive property allows us to break down the multiplication into simpler steps:
0.4 x 4 = 0.4 x (2 x 2) = (0.4 x 2) x 2 = 0.8 x 2 = 1.6
This method demonstrates how we can manipulate the numbers to make the calculation easier.
4. Repeated Addition:
Multiplication can be seen as repeated addition. Therefore:
0.4 x 4 = 0.4 + 0.4 + 0.4 + 0.4 = 1.6
This method is particularly helpful for visualizing the concept of multiplication.
Beyond the Calculation: Exploring the Concepts
While the answer to 0.4 x 4 is straightforward, the process reveals several crucial mathematical concepts:
-
Decimal Place Value: Understanding the place value of digits after the decimal point is paramount. Each place represents a decreasing power of 10 (tenths, hundredths, thousandths, etc.).
-
Fraction-Decimal Equivalence: The seamless conversion between decimals and fractions highlights their interconnectedness and provides alternative ways to solve problems.
-
Commutative Property of Multiplication: The order of the numbers doesn't affect the outcome (0.4 x 4 = 4 x 0.4).
-
Associative Property of Multiplication: The grouping of numbers doesn't change the result ((0.4 x 2) x 2 = 0.4 x (2 x 2)).
-
Distributive Property of Multiplication over Addition: This property allows for breaking down complex multiplication into simpler steps, making calculations more manageable.
Real-World Applications of Decimal Multiplication
The seemingly simple calculation of 0.4 x 4 has numerous real-world applications across various disciplines:
-
Finance: Calculating discounts (40% off an item costing $4), calculating interest on loans, determining the value of investments.
-
Engineering: Scaling down blueprints (reducing dimensions by 40%), calculating material quantities.
-
Science: Converting units (0.4 kilometers to meters), performing calculations involving measurements and proportions.
-
Cooking: Scaling recipes (using 0.4 times the ingredients), converting ingredient measurements.
-
Everyday Life: Calculating tips (40% tip on a $4 coffee), splitting bills among friends, working with unit prices in shopping.
Extending the Understanding: Moving Beyond 0.4 x 4
The principles applied in solving 0.4 x 4 can be easily extended to more complex decimal multiplications. For instance:
-
Multiplying decimals with multiple decimal places: The same principle of multiplying as if there were no decimal point and then adjusting the decimal place based on the total number of decimal places in the original numbers applies. For example, 0.25 x 3.2 would involve: 25 x 32 = 800. Since there are three total decimal places (two in 0.25 and one in 3.2), the decimal point is moved three places to the left, yielding 0.800 or 0.8.
-
Multiplying decimals by whole numbers greater than 4: The process remains identical. For example, 0.4 x 12 would be 4 x 12 = 48, and then adjusting the decimal point for one decimal place, resulting in 4.8.
-
Multiplying decimals by other decimals: Follow the same process: multiply as whole numbers and then place the decimal point based on the total number of decimal places in the factors.
Frequently Asked Questions (FAQ)
Q: What if I forget to account for the decimal point?
A: Forgetting to account for the decimal point will result in an incorrect answer that is often significantly larger than the actual value.
Q: Is there a quick way to estimate the answer to a decimal multiplication?
A: Yes, rounding the numbers to the nearest whole number can provide a quick estimate. For 0.4 x 4, rounding 0.4 to 0 gives an estimate of 0, while rounding it up to 1 gives an estimate of 4. The actual answer (1.6) falls between these estimates.
Q: Can I use a calculator for decimal multiplication?
A: Absolutely! Calculators are efficient tools for decimal multiplication, particularly when dealing with more complex numbers. However, understanding the underlying principles is crucial for problem-solving and developing numerical intuition.
Conclusion: Mastering the Fundamentals
The seemingly basic calculation of 0.4 x 4 opens a gateway to a deeper understanding of decimal arithmetic, fractional representation, and the fundamental properties of multiplication. While the answer itself is simple (1.6), the journey of solving it illuminates core mathematical concepts with wide-ranging practical applications. By understanding the methods, principles, and real-world relevance discussed here, learners can build a strong foundation in mathematics and approach more complex calculations with confidence and clarity. Remember that consistent practice and a solid grasp of fundamental concepts are key to mastering any mathematical skill. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
134lbs In Kg
Sep 15, 2025
-
96km In Miles
Sep 15, 2025
-
Feeding Past Tense
Sep 15, 2025
-
3ab 9ab 7ab
Sep 15, 2025
-
40 Of 250
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 0.4 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.