3ab 9ab 7ab
interactiveleap
Sep 15, 2025 · 5 min read
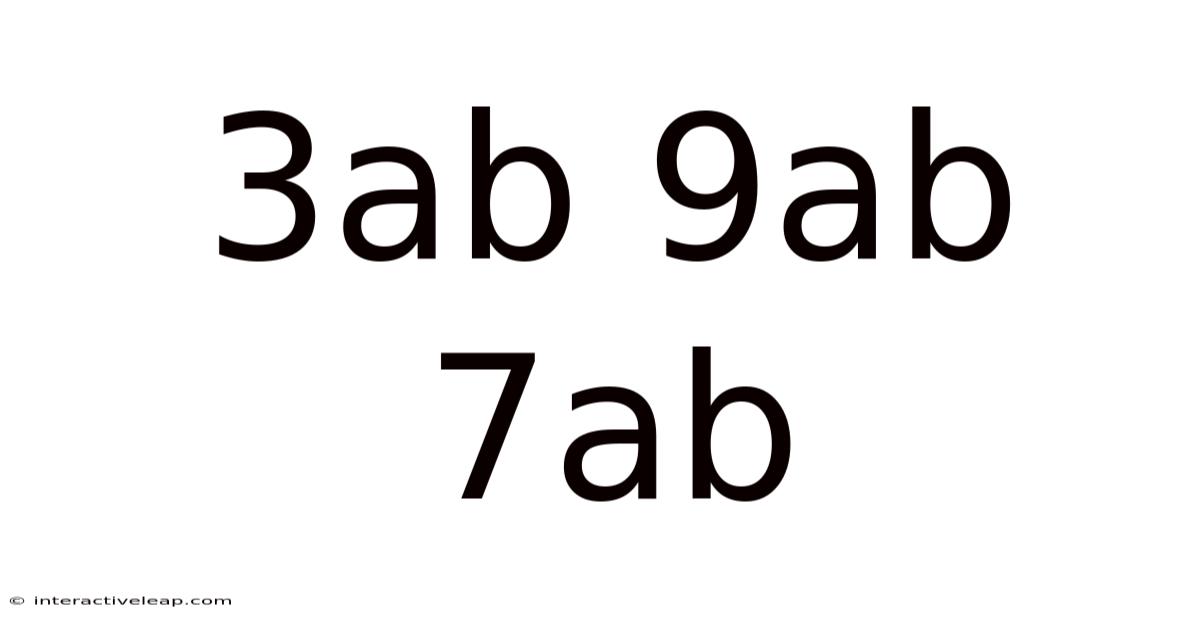
Table of Contents
Decoding the Mystery: A Deep Dive into 3ab, 9ab, and 7ab
This article delves into the intriguing world of algebraic expressions, specifically focusing on the seemingly simple yet surprisingly complex terms: 3ab, 9ab, and 7ab. While these might appear basic at first glance, understanding their nuances opens doors to a broader comprehension of algebra, its applications, and its inherent beauty. We'll explore their individual meanings, their relationships to each other, how they function within larger equations, and the fundamental concepts they represent. This exploration will be beneficial for students of all levels, from those just beginning their algebraic journey to those seeking a deeper understanding of fundamental mathematical principles.
Understanding the Basics: What do 3ab, 9ab, and 7ab Represent?
At their core, 3ab, 9ab, and 7ab are algebraic expressions representing the product of three elements: a coefficient, a variable 'a', and a variable 'b'. Let's break down each component:
-
Coefficient: The numerical value preceding the variables (3, 9, and 7 in our case). This coefficient signifies the number of times the variable terms are multiplied.
-
Variables: The letters 'a' and 'b' represent unknown values or quantities. In algebra, variables are placeholders, allowing us to work with general relationships rather than specific numbers. We can substitute specific numbers for 'a' and 'b' later to get a numerical result.
-
Product: The expression signifies that the coefficient and variables are multiplied together. So, 3ab means 3 * a * b, 9ab means 9 * a * b, and 7ab means 7 * a * b.
Therefore, these expressions aren't just numbers; they're concise ways of representing a multiplicative relationship between a constant and two variables.
Exploring Relationships: Comparing and Contrasting 3ab, 9ab, and 7ab
While 3ab, 9ab, and 7ab share a structural similarity, their coefficients differentiate them significantly. This difference affects their numerical value when specific values are assigned to 'a' and 'b'.
For instance, if a = 2 and b = 3:
- 3ab = 3 * 2 * 3 = 18
- 9ab = 9 * 2 * 3 = 54
- 7ab = 7 * 2 * 3 = 42
This simple example highlights the impact of the coefficient on the overall value of the expression. The larger the coefficient, the larger the resulting numerical value (assuming 'a' and 'b' remain constant).
Combining Like Terms: The Power of Simplification
One of the fundamental operations in algebra involves combining like terms. Like terms are expressions that have the same variables raised to the same powers. In our case, 3ab, 9ab, and 7ab are all like terms because they all consist of 'a' and 'b' raised to the power of 1.
This allows us to simplify expressions containing multiple instances of these like terms. For example, consider the expression:
3ab + 9ab - 7ab
Since these are like terms, we can simply add and subtract their coefficients:
(3 + 9 - 7)ab = 5ab
This simplification process significantly streamlines algebraic expressions, making them easier to manipulate and solve. The ability to combine like terms is a cornerstone of algebraic manipulation.
Beyond the Basics: Expanding the Scope
While 3ab, 9ab, and 7ab are elementary expressions, they serve as building blocks for more complex algebraic structures. They can appear within:
-
Polynomials: These are expressions with multiple terms, each involving variables raised to non-negative integer powers. Our terms could be part of a larger polynomial like: 5ab + 2a² + 7ab - 4b.
-
Equations: These expressions are used to represent relationships between variables. For example, 3ab + 5 = 14 would represent an equation where we need to solve for 'a' or 'b' (or both) given specific conditions.
-
Functions: In more advanced algebra, these terms can be used to define functions, which map inputs (values of 'a' and 'b') to outputs.
The seemingly simple 3ab, 9ab, and 7ab are therefore essential components in building and understanding more sophisticated algebraic structures and concepts.
Applications in Real-World Scenarios
While they may seem abstract, algebraic expressions like 3ab, 9ab, and 7ab have numerous applications in various real-world scenarios:
-
Area Calculations: If 'a' represents the length and 'b' represents the width of a rectangle, then expressions like 3ab could represent the area of three such rectangles.
-
Volume Calculations: Similarly, in three-dimensional scenarios, these expressions can represent the volume of a rectangular prism with dimensions related to 'a' and 'b'.
-
Physics and Engineering: Many physical phenomena are modeled using algebraic equations, and these expressions often appear within these equations. For instance, they could represent relationships between forces, velocities, or other physical quantities.
-
Economics and Finance: Economic models often utilize algebraic expressions to represent various relationships between variables like supply, demand, and profit.
Solving Equations Involving 3ab, 9ab, and 7ab
Let's look at an example of solving an equation involving these terms:
Example: Solve for 'a' if 3ab + 9ab = 36 and b = 2.
Solution:
-
Combine like terms: 3ab + 9ab = 12ab
-
Substitute the value of b: 12a(2) = 36
-
Simplify: 24a = 36
-
Solve for a: a = 36/24 = 3/2 = 1.5
This example demonstrates how even basic algebraic manipulations involving 3ab, 9ab, and 7ab can lead to practical solutions.
Frequently Asked Questions (FAQ)
Q1: What happens if 'a' or 'b' is equal to zero?
A1: If either 'a' or 'b' is zero, the entire expression (3ab, 9ab, or 7ab) becomes zero because anything multiplied by zero is zero.
Q2: Can these terms be negative?
A2: Yes, if either 'a' or 'b' (or both) is negative, the overall value of the expression will be negative. For example, if a = -2 and b = 3, then 3ab = -18.
Q3: What if we have exponents involved, like 3a²b or 9ab²?
A3: These are no longer like terms with 3ab, 9ab, and 7ab. Like terms must have the same variables raised to the same powers. 3a²b and 9ab² would require different simplification methods.
Conclusion: The Significance of Simplicity
Although 3ab, 9ab, and 7ab appear to be simple algebraic expressions, their significance extends far beyond their basic form. Understanding their structure, their relationships, and their manipulation is fundamental to grasping more complex algebraic concepts. They form the bedrock of algebraic reasoning, allowing us to represent and solve real-world problems across numerous disciplines. Mastering these seemingly simple expressions lays a crucial foundation for future success in mathematics and related fields. The journey into algebra starts with these building blocks, and a solid understanding of them is key to unlocking the deeper intricacies of this fascinating subject.
Latest Posts
Latest Posts
-
Staff In Training
Sep 15, 2025
-
45cm To M
Sep 15, 2025
-
10 M L
Sep 15, 2025
-
6th Square Number
Sep 15, 2025
-
Mg In Ml
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3ab 9ab 7ab . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.