6th Square Number
interactiveleap
Sep 15, 2025 · 6 min read
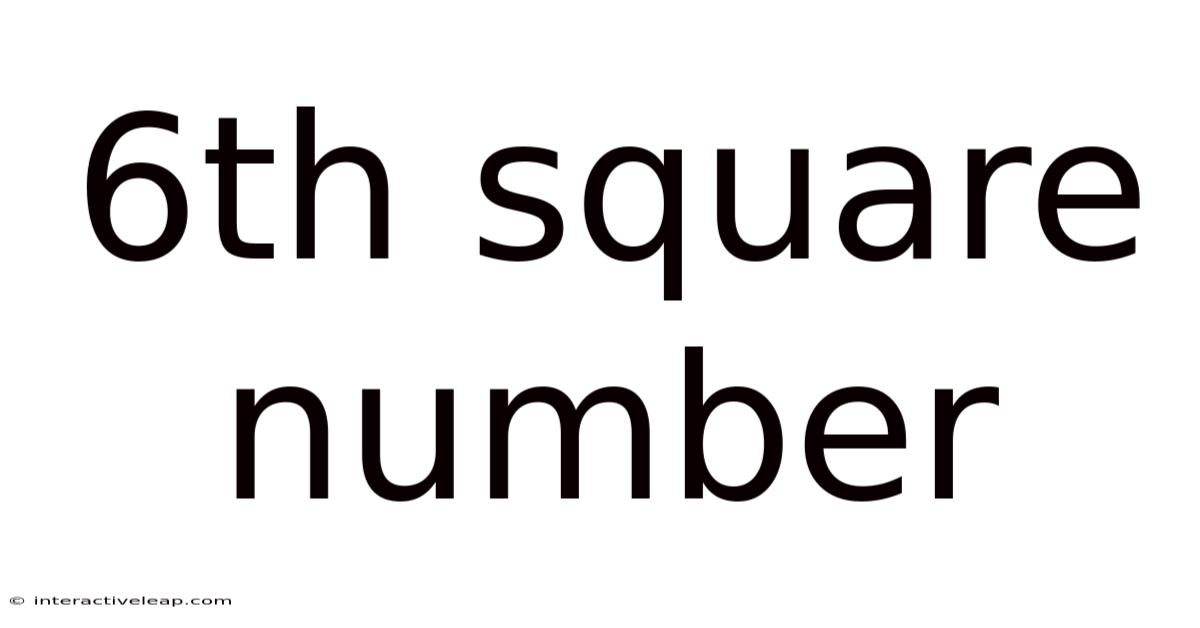
Table of Contents
Unveiling the Mysteries of the 6th Square Number: A Deep Dive into Square Numbers and Their Significance
The sixth square number, a seemingly simple concept in mathematics, opens a door to a fascinating world of patterns, sequences, and their applications in various fields. This article will delve into the intricacies of the sixth square number, exploring its calculation, its place within the sequence of square numbers, its properties, and its broader significance in mathematics and beyond. We will uncover its role in geometry, algebra, and even computer science, providing a comprehensive understanding accessible to all readers, regardless of their mathematical background. Understanding square numbers is fundamental to grasping many more complex mathematical concepts.
What is a Square Number?
Before we explore the specifics of the sixth square number, let's establish a solid foundation. A square number, also known as a perfect square, is a number that can be obtained by squaring (multiplying by itself) a whole number. In other words, it's the result of multiplying an integer by itself. For example:
- 1 x 1 = 1 (1 is a square number)
- 2 x 2 = 4 (4 is a square number)
- 3 x 3 = 9 (9 is a square number)
- and so on...
The sequence of square numbers begins 1, 4, 9, 16, 25, 36... Each number in this sequence represents the area of a square with sides of integer length. This geometrical interpretation is crucial to understanding the concept intuitively.
Calculating the 6th Square Number
Now, let's focus on our main subject: the sixth square number. To find it, we simply need to square the sixth whole number, which is 6. Therefore:
6 x 6 = 36
The sixth square number is 36.
The Significance of 36: Exploring its Properties
36, as the sixth square number, holds several interesting mathematical properties:
-
Divisors: 36 has a relatively large number of divisors (1, 2, 3, 4, 6, 9, 12, 18, 36). This makes it a highly composite number, meaning it has more divisors than any smaller positive integer.
-
Factors: The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. Analyzing these factors reveals further patterns and relationships.
-
Sum of Divisors: The sum of the divisors of 36 (excluding 36 itself) is 1+2+3+4+6+9+12+18 = 55. This sum is greater than 36, classifying it as an abundant number.
-
Geometric Representation: As mentioned earlier, 36 represents the area of a square with sides of length 6 units. This geometrical interpretation provides a visual understanding of the concept. Imagine a 6x6 grid; it contains 36 squares.
-
Relationship to other numbers: 36 is also related to other mathematical concepts, such as triangular numbers (sum of consecutive integers) and perfect numbers (numbers equal to the sum of their proper divisors). While 36 itself isn't a perfect number, its factors and divisors play a role in the properties of other numbers within these sequences.
Square Numbers in Geometry and Algebra
Square numbers have profound implications in both geometry and algebra:
-
Geometry: As discussed, square numbers directly represent the areas of squares with integer side lengths. This relationship extends to other geometric shapes and calculations involving areas and volumes. Understanding square numbers is fundamental to understanding more complex geometric problems.
-
Algebra: Square numbers are frequently encountered in algebraic equations and formulas. They appear in quadratic equations, Pythagorean theorem calculations, and various other mathematical expressions. Mastering the concept of square numbers is essential for success in algebra and higher-level mathematics.
Applications of Square Numbers in Real-World Scenarios
The applications of square numbers extend beyond the theoretical realm and find practical use in various fields:
-
Construction and Engineering: Square numbers are crucial in construction and engineering for calculating areas, volumes, and dimensions. From laying out foundations to designing structures, the concept of square numbers is integral to accurate measurements and calculations.
-
Computer Science: In computer science, square numbers are used in algorithms and data structures. For instance, they play a role in matrix operations and array manipulations.
-
Game Design: Square numbers frequently appear in game design, particularly in grid-based games like chess or board games. The properties of square numbers can be leveraged to create balanced and strategic game mechanics.
-
Data Analysis and Statistics: Square numbers are used in statistical calculations, particularly in variance and standard deviation calculations. Understanding square numbers aids in interpreting data and drawing meaningful conclusions.
The Sequence of Square Numbers: Patterns and Relationships
The sequence of square numbers itself exhibits fascinating patterns and relationships:
-
Differences between consecutive squares: The differences between consecutive square numbers form an arithmetic sequence: 3, 5, 7, 9, 11... This pattern is based on the odd numbers.
-
Sum of consecutive odd numbers: Each square number can be expressed as the sum of consecutive odd numbers, starting from 1. For example:
- 1 = 1
- 4 = 1 + 3
- 9 = 1 + 3 + 5
- 16 = 1 + 3 + 5 + 7
- and so on…
-
Visual Representation: The sequence can be visually represented using dots arranged in squares. This visual representation helps to understand the growth pattern of square numbers and their connection to geometry.
Frequently Asked Questions (FAQs)
Q1: What is the formula for calculating a square number?
A1: The formula for calculating the nth square number is n². For example, the 6th square number is 6² = 36.
Q2: Are all square numbers even?
A2: No, square numbers can be either even or odd. If the base number (n) is even, the square number (n²) will be even. If the base number is odd, the square number will also be odd.
Q3: What is the relationship between square numbers and triangular numbers?
A3: There is a fascinating relationship between square numbers and triangular numbers. The sum of two consecutive triangular numbers always equals a square number.
Q4: Are there any applications of square numbers in physics?
A4: Yes, square numbers appear in various physics formulas and calculations, particularly in areas dealing with areas, volumes, and forces.
Conclusion: The Enduring Significance of Square Numbers
The sixth square number, 36, is more than just a simple numerical value. It represents a fundamental concept in mathematics with far-reaching applications in various fields. From its geometric interpretation to its algebraic significance and its practical applications in real-world scenarios, understanding square numbers provides a solid foundation for grasping more advanced mathematical principles. The patterns and relationships within the sequence of square numbers offer further insights into the elegance and beauty of mathematics, underscoring the enduring importance of this seemingly simple concept. By exploring the properties of 36 and its place within the larger context of square numbers, we've gained a deeper appreciation for the interconnectedness of mathematical concepts and their relevance to our world. The journey of understanding square numbers is a testament to the power of mathematical exploration and the beauty of patterns found in seemingly simple numerical sequences.
Latest Posts
Latest Posts
-
Opposite Of Meek
Sep 15, 2025
-
4 8m In Cm
Sep 15, 2025
-
80 Of 200
Sep 15, 2025
-
53 3kg To Stone
Sep 15, 2025
-
85kh In Stone
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 6th Square Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.