33 X 4
interactiveleap
Sep 15, 2025 · 5 min read
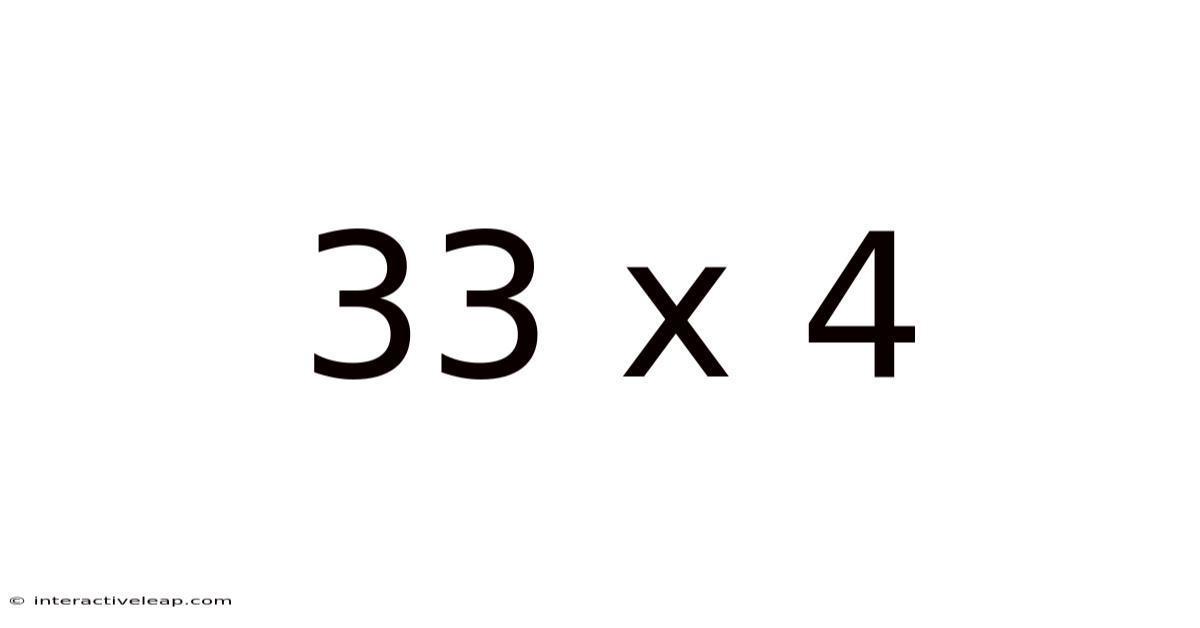
Table of Contents
Decoding 33 x 4: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem, 33 x 4, transforming it into a gateway to understanding fundamental mathematical concepts, practical applications, and even the beauty of numerical patterns. We'll move beyond the simple answer and delve into the "why" behind the calculation, exploring various methods, real-world examples, and related mathematical principles. This journey will be accessible to all, from elementary school students to those seeking a refresher or a deeper appreciation for the elegance of mathematics.
Introduction: More Than Just an Answer
At first glance, 33 x 4 appears trivial. A quick calculation reveals the answer: 132. But let's resist the urge to stop there. This seemingly simple equation provides a fertile ground for exploring several core mathematical concepts and their practical applications. This article aims to unravel the layers of understanding behind this basic multiplication problem, making it relevant and engaging for learners of all levels.
Method 1: The Traditional Approach – Long Multiplication
The most common method taught in schools is long multiplication. Let's break down 33 x 4 step-by-step:
-
Multiply the ones: 4 x 3 (the ones digit of 33) = 12. Write down '2' and carry-over '1'.
-
Multiply the tens: 4 x 3 (the tens digit of 33) = 12. Add the carried-over '1' to get 13.
-
Combine the results: The final answer is 132.
This method emphasizes place value – the position of a digit determining its value (ones, tens, hundreds, etc.) – a crucial concept in understanding larger numbers and more complex calculations.
Method 2: Distributive Property – Breaking it Down
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this to simplify 33 x 4:
- Rewrite 33 as 30 + 3.
- Apply the distributive property: 4 x (30 + 3) = (4 x 30) + (4 x 3) = 120 + 12 = 132.
This approach demonstrates a fundamental algebraic principle and provides an alternative method for solving the problem, particularly useful for larger numbers where mental calculations might be challenging.
Method 3: Repeated Addition – Back to the Basics
Multiplication is essentially repeated addition. 33 x 4 can be visualized as adding 33 four times:
33 + 33 + 33 + 33 = 132
This method reinforces the core relationship between addition and multiplication, making it especially helpful for younger learners still grasping the concept of multiplication.
Real-World Applications of 33 x 4
While seemingly abstract, the concept of multiplication – and thus 33 x 4 – has numerous real-world applications:
-
Shopping: Imagine buying 4 items that cost $33 each. The total cost would be 33 x 4 = $132.
-
Construction: A construction project might require 4 sets of 33 bricks. Knowing 33 x 4 = 132 helps determine the total number of bricks needed.
-
Baking: A recipe calls for 4 batches of a mixture, each requiring 33 grams of flour. The total amount of flour needed is 33 x 4 = 132 grams.
-
Travel: If a car travels at an average speed of 33 miles per hour for 4 hours, the total distance covered would be 33 x 4 = 132 miles.
These scenarios highlight how multiplication is not just a classroom exercise, but a practical tool used daily in various contexts.
Exploring Related Mathematical Concepts
The seemingly simple problem of 33 x 4 provides a springboard to exploring several interconnected mathematical concepts:
-
Factors and Multiples: The numbers 33 and 4 are factors of 132. 132 is a multiple of 33 and 4. Understanding factors and multiples is crucial for simplifying fractions, solving equations, and understanding number theory.
-
Prime Factorization: Breaking down a number into its prime factors (numbers divisible only by 1 and themselves) provides a deeper understanding of the number's structure. While 33 and 4 are not prime, understanding prime factorization is vital for advanced mathematical concepts like cryptography.
-
Divisibility Rules: Knowing divisibility rules helps quickly determine if a number is divisible by another without performing long division. For example, 132 is divisible by 2 (because it's an even number), 3 (because the sum of its digits, 1+3+2=6, is divisible by 3), and 4 (because the last two digits, 32, are divisible by 4).
-
Algebraic Expressions: The distributive property demonstrates the connection between arithmetic and algebra, laying the groundwork for more complex algebraic manipulation.
Expanding the Scope: Beyond 33 x 4
While we've focused on 33 x 4, the principles discussed apply to all multiplication problems. Let’s consider similar problems to solidify our understanding:
-
33 x 8: This can be solved as (33 x 4) x 2 = 132 x 2 = 264, showcasing the associative property of multiplication.
-
66 x 4: This is double 33 x 4, demonstrating the relationship between doubling and multiplication.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate 33 x 4?
A: The easiest way depends on individual preference and skill level. Long multiplication is systematic, while the distributive property offers a different approach. Repeated addition is great for visualization, particularly for beginners.
Q: Are there other methods to solve 33 x 4 besides the ones mentioned?
A: Yes, various mental math techniques can be used, like breaking down 33 into smaller numbers (e.g., 30 + 3) and multiplying each part separately before adding the results.
Q: Why is understanding place value important in multiplication?
A: Place value ensures that each digit contributes its correct value to the overall calculation, avoiding errors in larger multiplication problems.
Q: How does this relate to more advanced mathematics?
A: The principles of multiplication, including the distributive property and understanding of factors and multiples, form the foundation for advanced mathematical concepts like algebra, calculus, and number theory.
Conclusion: The Enduring Power of a Simple Equation
The seemingly simple problem of 33 x 4 offers a rich learning experience. It's not merely about obtaining the answer (132) but about understanding the underlying mathematical principles, exploring different calculation methods, and appreciating the multifaceted applications of multiplication in everyday life. By breaking down this seemingly simple problem, we've unearthed a wealth of mathematical concepts and demonstrated its real-world relevance. The journey of understanding 33 x 4 extends far beyond the immediate calculation, opening doors to a deeper appreciation of mathematics and its power to solve problems in diverse contexts. From the basic building blocks of addition to the elegant properties of distribution and the far-reaching application of place value, the exploration of 33 x 4 serves as a powerful microcosm of mathematical understanding.
Latest Posts
Latest Posts
-
Kinetic Energy Calculator
Sep 15, 2025
-
Half Of 55
Sep 15, 2025
-
Mmolar To Um
Sep 15, 2025
-
0 75 X 5
Sep 15, 2025
-
134lbs In Kg
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 33 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.