0.75 X 5
interactiveleap
Sep 15, 2025 · 5 min read
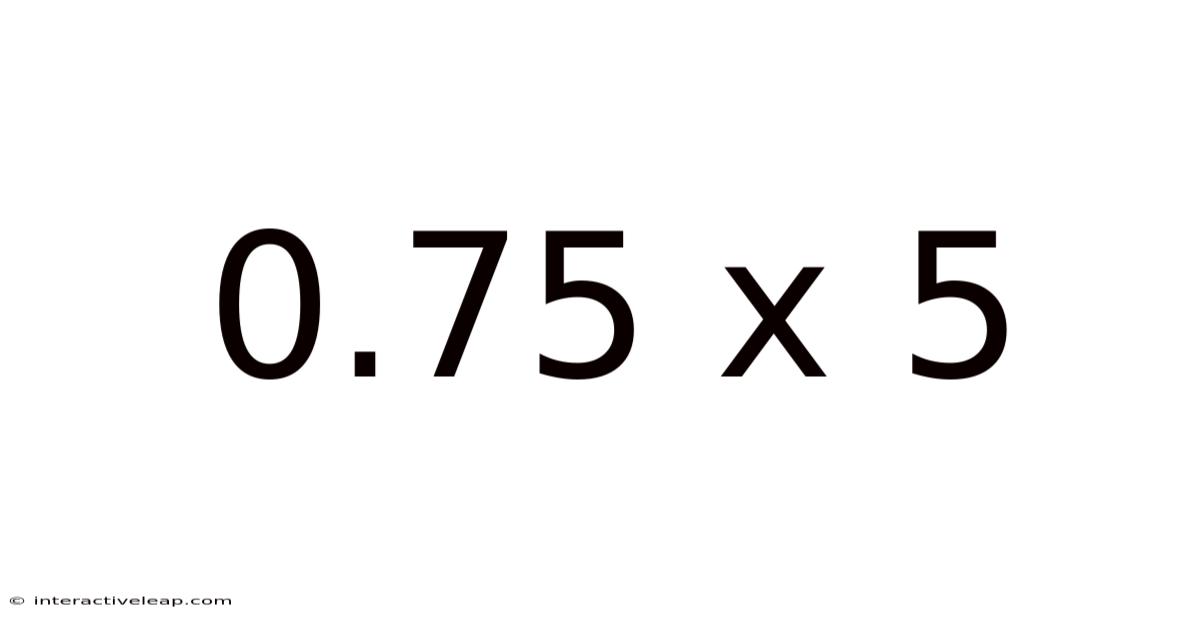
Table of Contents
Unveiling the Simplicity and Power of 0.75 x 5: A Deep Dive into Multiplication
This article explores the seemingly simple calculation of 0.75 multiplied by 5, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine different methods for solving this problem, demonstrating various approaches suitable for diverse learning styles and mathematical backgrounds. Understanding this seemingly basic calculation forms a crucial foundation for more complex mathematical concepts. This exploration will be particularly beneficial for students learning fractions, decimals, and multiplication.
Understanding the Components: Decimals and Fractions
Before diving into the multiplication itself, let's clarify the components: 0.75 and 5.
0.75 (or Three-Quarters): This is a decimal representation of a fraction. It signifies seventy-five hundredths, meaning 75 parts out of 100. Equivalently, it can be expressed as the fraction ¾ (three-quarters). Understanding this equivalence is key to solving this problem using multiple approaches.
5: This is a whole number, representing five units.
Method 1: Direct Decimal Multiplication
The most straightforward method involves directly multiplying the decimal by the whole number:
0.75 x 5 = 3.75
This can be done using standard multiplication techniques, either manually or with a calculator. The calculation proceeds as follows:
5 x 75 = 375
Since we are multiplying by a decimal with two places after the decimal point (0.75), we move the decimal point two places to the left in the result (375), giving us 3.75.
Method 2: Fractional Multiplication
Converting the decimal 0.75 to its fractional equivalent, ¾, provides an alternative approach. This method is particularly useful for building a strong understanding of fraction manipulation.
The calculation becomes:
¾ x 5
We can rewrite 5 as ⁵⁄₁ (five over one), turning the problem into:
¾ x ⁵⁄₁ = ¹⁵⁄₄
Now, we simplify the improper fraction ¹⁵⁄₄ by dividing the numerator (15) by the denominator (4):
15 ÷ 4 = 3 with a remainder of 3
This gives us a mixed number: 3 ¾
Finally, we convert this mixed number back to a decimal:
3 ¾ = 3 + 0.75 = 3.75
Method 3: Repeated Addition
For those who prefer a more visual and intuitive approach, repeated addition provides a clear understanding of multiplication. Multiplication is essentially repeated addition. Therefore, 0.75 x 5 can be interpreted as adding 0.75 five times:
0.75 + 0.75 + 0.75 + 0.75 + 0.75 = 3.75
This method is especially helpful for visualizing the concept of multiplication, particularly for younger learners.
Method 4: Distributive Property
The distributive property of multiplication over addition can also be applied. We can break down 0.75 into 0.5 + 0.25 and then multiply each part by 5 separately:
(0.5 + 0.25) x 5 = (0.5 x 5) + (0.25 x 5) = 2.5 + 1.25 = 3.75
This approach highlights the flexibility of mathematical operations and reinforces the understanding of the distributive property.
The Significance of 0.75 x 5: Real-World Applications
While seemingly a simple mathematical exercise, understanding the calculation of 0.75 x 5 has various practical applications:
-
Calculating Discounts: If an item is discounted by 75%, and the original price is $5, this calculation directly provides the discount amount ($3.75).
-
Portioning Ingredients: If a recipe calls for ¾ of a cup of an ingredient and you need to make five batches, this calculation determines the total amount of the ingredient required (3.75 cups).
-
Financial Calculations: This calculation can be applied to interest calculations, profit margins, and various other financial scenarios involving percentages and fractions.
-
Geometric Problems: Calculating areas or volumes involving fractions of units often necessitates this type of calculation.
Extending the Concept: Variations and Further Exploration
The understanding gained from solving 0.75 x 5 can be extended to various related problems:
-
Multiplying by other whole numbers: Applying the same methods to other whole numbers helps solidify the understanding of decimal and fractional multiplication.
-
Multiplying by other decimals: Extending the principles to other decimal multiplications strengthens the understanding of decimal place values.
-
Solving for unknowns: Problems involving unknowns (e.g., x x 5 = 3.75) reinforce problem-solving skills and the relationship between multiplication and division.
-
Understanding Percentages: The connection between decimals, fractions, and percentages allows for more versatile problem-solving across different contexts.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate 0.75 x 5?
A: The easiest way depends on individual preference and understanding. Direct decimal multiplication is often the fastest, but the repeated addition method offers a strong conceptual understanding.
Q: Why is converting to fractions helpful?
A: Converting to fractions helps build a strong foundation in understanding fractional arithmetic and the relationship between fractions and decimals.
Q: Can I use a calculator?
A: Yes, a calculator provides a quick solution, but understanding the underlying mathematical principles is crucial for developing a strong mathematical foundation.
Q: What if I need to multiply 0.75 by a larger number?
A: The same methods can be applied. The complexity might increase slightly with larger numbers, but the underlying principles remain the same.
Conclusion: Beyond the Numbers
The seemingly straightforward calculation of 0.75 x 5 offers a gateway to a deeper understanding of decimals, fractions, and fundamental mathematical principles. Mastering this seemingly simple calculation builds a solid foundation for more advanced mathematical concepts and empowers individuals to confidently tackle diverse real-world problems involving fractions, decimals, and percentages. The different methods explored here—direct multiplication, fractional multiplication, repeated addition, and the distributive property—cater to various learning styles, ensuring that the concept is readily grasped and retained. By understanding not just the answer (3.75), but also the how and why behind the calculation, we unlock a much more profound appreciation for the power and elegance of mathematics.
Latest Posts
Latest Posts
-
Exam In French
Sep 15, 2025
-
Tbsp To Ounces
Sep 15, 2025
-
Staff In Training
Sep 15, 2025
-
45cm To M
Sep 15, 2025
-
10 M L
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 0.75 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.