X 6 2
interactiveleap
Sep 16, 2025 · 6 min read
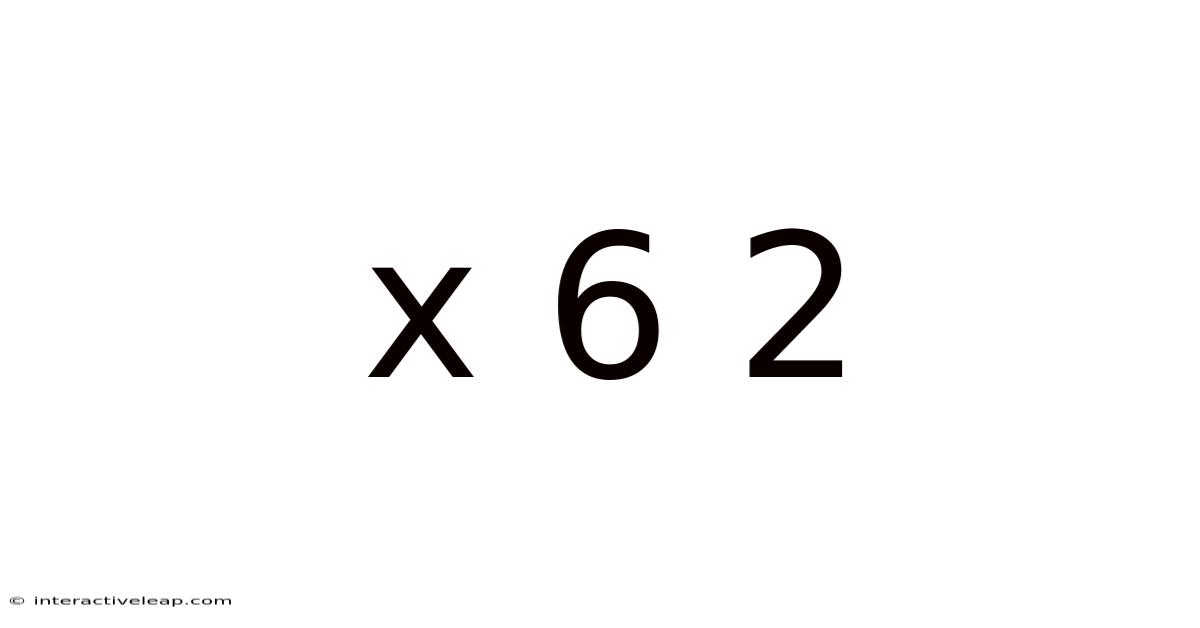
Table of Contents
Decoding X^6 * 2: A Deep Dive into Exponential Functions and Their Applications
This article delves into the mathematical expression X<sup>6</sup> * 2, exploring its meaning, calculation methods, practical applications, and related concepts. We'll examine the underlying principles of exponents, their significance in various fields, and address common questions surrounding this specific expression. Understanding X<sup>6</sup> * 2 is key to grasping fundamental algebraic concepts and their real-world relevance.
Introduction: Understanding the Fundamentals
The expression X<sup>6</sup> * 2 represents a combination of two core mathematical operations: exponentiation and multiplication. Let's break down each component:
-
Exponentiation (X<sup>6</sup>): This signifies X multiplied by itself six times (X * X * X * X * X * X). The number 6 is called the exponent or power, and X is the base. The exponent dictates how many times the base is multiplied by itself.
-
Multiplication ( 2):* This is a straightforward operation where the result of the exponentiation (X<sup>6</sup>) is multiplied by 2.
Therefore, X<sup>6</sup> * 2 is a concise way of representing a more complex calculation. The specific numerical value of this expression depends entirely on the value assigned to X.
Calculating X<sup>6</sup> * 2: Step-by-Step Guide
Calculating the value of X<sup>6</sup> * 2 involves a simple two-step process:
-
Exponentiation: Calculate X raised to the power of 6 (X<sup>6</sup>). This can be done manually for small values of X or using a calculator or computer program for larger or more complex values.
-
Multiplication: Once X<sup>6</sup> is determined, multiply the result by 2.
Example: Let's say X = 3. Here's how we'd calculate X<sup>6</sup> * 2:
-
Exponentiation: 3<sup>6</sup> = 3 * 3 * 3 * 3 * 3 * 3 = 729
-
Multiplication: 729 * 2 = 1458
Therefore, when X = 3, X<sup>6</sup> * 2 = 1458.
Expanding the Understanding: Properties of Exponents
To fully grasp the implications of X<sup>6</sup> * 2, understanding the properties of exponents is crucial. These properties allow for simplification and efficient calculations:
-
Product of Powers: When multiplying two expressions with the same base, you add the exponents. For example, X<sup>a</sup> * X<sup>b</sup> = X<sup>(a+b)</sup>.
-
Quotient of Powers: When dividing two expressions with the same base, you subtract the exponents. For example, X<sup>a</sup> / X<sup>b</sup> = X<sup>(a-b)</sup>.
-
Power of a Power: When raising an expression with an exponent to another power, you multiply the exponents. For example, (X<sup>a</sup>)<sup>b</sup> = X<sup>(a*b)</sup>.
-
Power of a Product: When raising a product to a power, you raise each factor to that power. For example, (X * Y)<sup>a</sup> = X<sup>a</sup> * Y<sup>a</sup>.
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power. For example, (X / Y)<sup>a</sup> = X<sup>a</sup> / Y<sup>a</sup>.
These properties are invaluable for simplifying complex expressions involving exponents, making calculations easier and more manageable.
Real-World Applications of Exponential Functions
Exponential functions, like the one represented in X<sup>6</sup> * 2, are not merely abstract mathematical concepts; they have extensive applications in various fields:
-
Compound Interest: The growth of money invested with compound interest follows an exponential function. The formula for compound interest involves an exponent representing the number of compounding periods.
-
Population Growth: Modeling population growth, whether it's human populations, bacterial colonies, or animal populations, often utilizes exponential functions. The rate of growth is usually proportional to the current population size.
-
Radioactive Decay: The decay of radioactive substances follows an exponential function, where the amount remaining decreases exponentially over time. This is crucial in fields like nuclear physics and medicine.
-
Computer Science: Exponential functions are fundamental in analyzing algorithm efficiency. Algorithms with exponential time complexity become computationally impractical for large input sizes.
-
Physics: Many physical phenomena, like the intensity of light decreasing with distance or the rate of cooling of an object, can be modeled using exponential functions.
-
Engineering: Exponential functions play a crucial role in various engineering disciplines, such as electrical engineering (circuit analysis) and mechanical engineering (vibration analysis).
Solving Equations Involving X<sup>6</sup> * 2
The expression X<sup>6</sup> * 2 can be part of more complex equations that require solving for X. For example, consider the equation:
X<sup>6</sup> * 2 = 128
To solve this equation, we need to isolate X:
-
Divide both sides by 2: X<sup>6</sup> = 64
-
Take the sixth root of both sides: X = <sup>6</sup>√64 (The sixth root is the inverse operation of raising to the power of 6).
-
Solve for X: X = 2
Therefore, the solution to the equation X<sup>6</sup> * 2 = 128 is X = 2. Solving more complex equations involving X<sup>6</sup> * 2 might require advanced algebraic techniques or numerical methods.
Beyond the Basics: Exploring Higher-Order Polynomials
The expression X<sup>6</sup> * 2 is a simple example of a polynomial, a mathematical expression involving variables raised to non-negative integer powers. While this specific expression is relatively straightforward, understanding it is crucial for tackling more complex polynomials. Polynomials are essential in:
-
Curve Fitting: Polynomials of various degrees can be used to fit curves to data points, which is crucial in many scientific and engineering applications.
-
Calculus: Polynomials are fundamental in calculus, forming the basis for many differentiation and integration techniques.
-
Numerical Analysis: Polynomials are widely used in numerical analysis for approximating functions and solving equations.
Frequently Asked Questions (FAQ)
-
Q: What if X is a negative number? A: If X is negative, X<sup>6</sup> will be positive because an even exponent eliminates the negative sign. The final result, X<sup>6</sup> * 2, will also be positive.
-
Q: Can X be zero? A: Yes, if X = 0, then X<sup>6</sup> = 0, and X<sup>6</sup> * 2 = 0.
-
Q: Can X be a fraction or decimal? A: Yes, X can be any real number, including fractions and decimals. The calculation will be more complex, but the principles remain the same.
-
Q: How do I calculate X<sup>6</sup> for large values of X? A: For large values of X, a calculator or computer software is recommended for efficient and accurate calculation.
Conclusion: The Significance of X<sup>6</sup> * 2
While seemingly simple, the expression X<sup>6</sup> * 2 provides a gateway to understanding fundamental mathematical concepts like exponentiation, polynomial functions, and their far-reaching applications. Mastering these principles is crucial for success in various academic and professional fields. The ability to manipulate and solve equations involving such expressions is essential for problem-solving across diverse disciplines, highlighting the practical relevance of even seemingly basic mathematical constructs. This deep dive underscores the significance of understanding not just the calculation itself, but also the underlying theoretical framework that supports it, emphasizing the interconnected nature of mathematical concepts and their real-world implications. The continued exploration of these concepts will undoubtedly lead to a greater appreciation of the power and elegance of mathematics.
Latest Posts
Latest Posts
-
155lbs To Stone
Sep 16, 2025
-
56 3 Kg Pounds
Sep 16, 2025
-
3 X 90
Sep 16, 2025
-
27 X 3
Sep 16, 2025
-
30 Of 18
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 6 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.