27 X 3
interactiveleap
Sep 16, 2025 · 5 min read
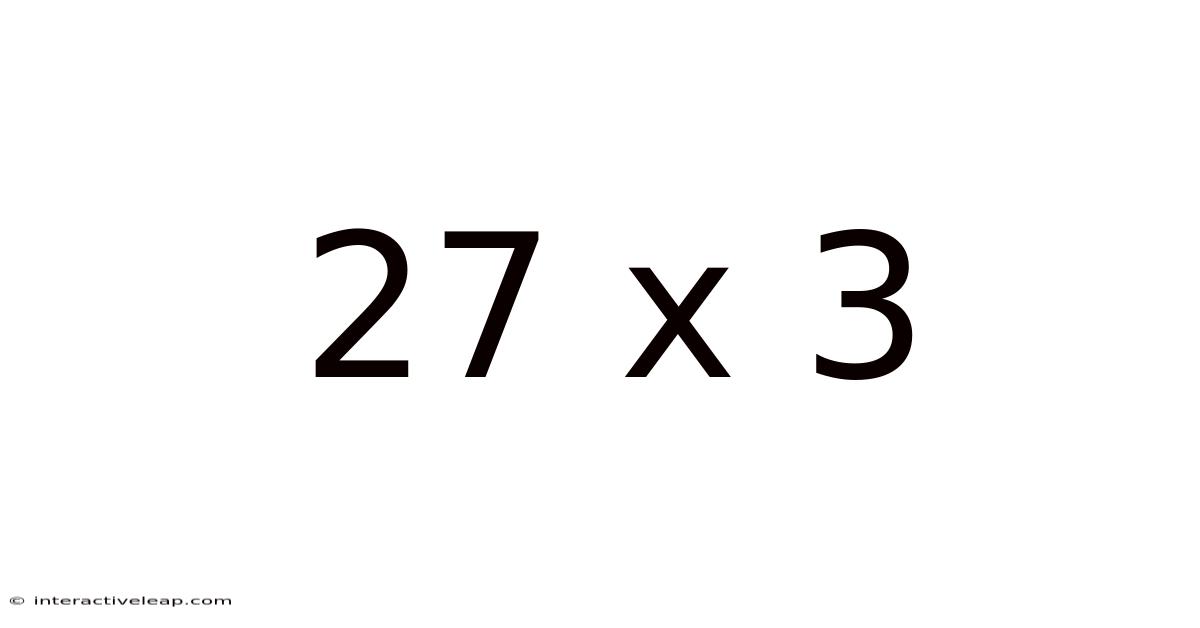
Table of Contents
Unveiling the Wonders of 27 x 3: A Deep Dive into Multiplication
This article delves into the seemingly simple multiplication problem of 27 x 3, exploring its various facets, from basic calculation to its applications in real-world scenarios and advanced mathematical concepts. We'll uncover the beauty of this fundamental arithmetic operation, showcasing its importance in building a strong mathematical foundation. This exploration goes beyond a simple answer, providing a comprehensive understanding that empowers you to tackle more complex mathematical challenges. This detailed guide is perfect for students, educators, and anyone curious to explore the world of numbers.
Understanding the Fundamentals: Basic Multiplication
At its core, 27 x 3 represents repeated addition. It signifies adding the number 27 to itself three times: 27 + 27 + 27. This fundamental understanding forms the bedrock of multiplication and is crucial for grasping more advanced mathematical concepts.
To calculate 27 x 3, we can use several methods. The most straightforward approach is through the standard multiplication algorithm learned in elementary school:
27
x 3
----
81
This algorithm involves multiplying each digit of 27 by 3, starting with the ones place (7 x 3 = 21). The 1 is written down, and the 2 is carried over to the tens place. Next, we multiply the tens place (2 x 3 = 6) and add the carried-over 2 (6 + 2 = 8). This results in the final answer: 81.
Beyond the Algorithm: Exploring Different Approaches
While the standard algorithm is efficient, understanding alternative methods enhances comprehension and problem-solving skills.
-
Distributive Property: We can break down 27 into 20 + 7. This allows us to apply the distributive property of multiplication: 3 x (20 + 7) = (3 x 20) + (3 x 7) = 60 + 21 = 81. This method demonstrates a deeper understanding of how multiplication works, making it easier to tackle more complex equations.
-
Repeated Addition: As mentioned earlier, 27 x 3 is equivalent to 27 + 27 + 27. Manually adding these numbers will also yield the correct answer of 81. This approach is especially helpful for visualizing the concept of multiplication.
-
Using a Number Line: A visual representation on a number line can be beneficial, particularly for younger learners. Starting at 0, you would jump 27 units three times, ending up at 81. This method helps solidify the connection between addition and multiplication.
-
Estimation: Before performing the calculation, estimating the answer provides a valuable check. Rounding 27 to 30, we get 30 x 3 = 90. This estimate gives us a reasonable expectation of the actual answer, helping to identify potential errors.
Real-World Applications: Where 27 x 3 Comes to Life
The multiplication problem 27 x 3 is not confined to the realm of abstract mathematics. It finds its place in various everyday scenarios:
-
Shopping: Imagine buying three items that cost $27 each. The total cost would be 27 x 3 = $81.
-
Measurement: If you need three pieces of wood, each 27 inches long, the total length required would be 81 inches.
-
Inventory Management: A warehouse might have three stacks of boxes, each containing 27 items. The total number of items would be 81.
-
Recipe Scaling: If a recipe calls for 27 grams of flour and you need to triple the recipe, you would require 81 grams of flour.
These examples highlight the practical applicability of basic multiplication in everyday situations, emphasizing its relevance beyond the classroom.
Diving Deeper: Exploring Advanced Concepts
While 27 x 3 might seem basic, exploring its context within advanced mathematical concepts can deepen our understanding.
-
Factors and Multiples: 27 and 3 are factors of 81, meaning they divide 81 without leaving a remainder. Conversely, 81 is a multiple of both 27 and 3. Understanding factors and multiples is foundational for working with fractions, ratios, and algebraic equations.
-
Prime Factorization: The prime factorization of 81 is 3 x 3 x 3 x 3 (or 3⁴). This concept helps in simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM) of numbers.
-
Modular Arithmetic: In modular arithmetic, we look at remainders after division. For example, 81 modulo 5 (written as 81 mod 5) is 1, as 81 divided by 5 leaves a remainder of 1. Modular arithmetic has extensive applications in cryptography and computer science.
-
Algebra: The concept of multiplication extends to algebraic expressions. For example, 3(x + 9) can be expanded using the distributive property, a direct application of the method used to solve 27 x 3.
Addressing Common Questions (FAQs)
-
Q: What is the easiest way to multiply 27 by 3?
- A: The standard multiplication algorithm is generally the easiest and most efficient method for most people. However, the distributive property offers a valuable alternative that enhances understanding.
-
Q: Are there any tricks to memorizing multiplication facts involving 27?
- A: While there aren't specific tricks solely for 27, practicing multiplication tables regularly and understanding the underlying principles of multiplication are crucial for memorization.
-
Q: How can I help my child learn multiplication?
- A: Use a variety of methods, including visual aids (number lines, blocks), real-world examples, and games. Make it interactive and engaging, focusing on understanding the concept rather than rote memorization.
-
Q: Why is understanding multiplication important?
- A: Multiplication is a fundamental building block of mathematics. It forms the basis for many more advanced concepts and has practical applications in various fields, including science, engineering, and finance.
Conclusion: The Significance of a Simple Equation
While 27 x 3 may appear as a simple arithmetic problem, its exploration unveils a wealth of mathematical concepts and practical applications. From basic calculation methods to advanced mathematical principles, this seemingly straightforward equation serves as a microcosm of the larger world of mathematics. By understanding its various aspects, we build a stronger foundation for tackling more complex challenges and appreciating the beauty and elegance of mathematics in our everyday lives. The journey of understanding 27 x 3 is not just about arriving at the answer 81; it’s about the process of learning, exploring, and connecting seemingly disparate mathematical ideas, ultimately fostering a deeper appreciation for the power and utility of numbers. Remember, the key to mastering mathematics lies in understanding the underlying principles, and 27 x 3 provides a perfect platform to develop that understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about 27 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.