X 5 4
interactiveleap
Sep 22, 2025 · 6 min read
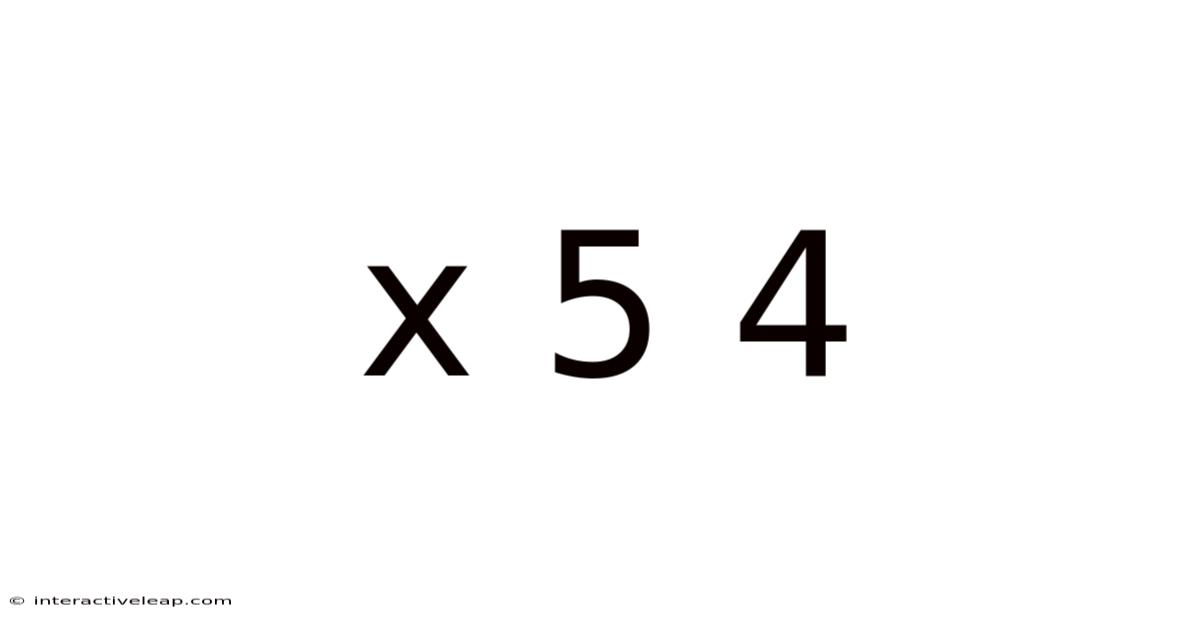
Table of Contents
Decoding the Mystery: Exploring the Mathematical Significance of x⁵ + 4
This article delves into the intriguing mathematical expression x⁵ + 4, exploring its properties, factorization, and broader implications within algebra and number theory. We'll uncover its secrets, unravel its complexities, and demonstrate its relevance beyond a simple algebraic equation. Understanding this expression provides valuable insights into polynomial factorization, complex numbers, and the elegance of mathematical relationships.
Introduction: A Seemingly Simple Expression
At first glance, x⁵ + 4 appears to be a straightforward polynomial expression. However, its factorization reveals a surprising depth and connection to the realm of complex numbers. This exploration will move beyond simple algebraic manipulation to uncover the underlying mathematical principles that govern its behavior. We'll discover how seemingly simple expressions can lead to complex and rewarding mathematical discoveries. The key to understanding x⁵ + 4 lies in mastering the techniques of polynomial factorization and embracing the world of complex numbers.
Factorization Techniques: Unraveling the Expression
The immediate challenge is to factor x⁵ + 4. Traditional methods like factoring by grouping or using the quadratic formula won't directly work. The key lies in employing the sum of cubes formula, a powerful tool in algebraic manipulation, but with a crucial twist involving complex numbers.
Remember the sum of cubes formula: a³ + b³ = (a + b)(a² - ab + b²). While this doesn't directly apply to x⁵ + 4, we can cleverly manipulate the expression to make it applicable.
Let's consider x⁵ + 4 as x⁵ + 2⁵. However, the standard sum of cubes formula requires a cube, not a fifth power. To overcome this, we introduce complex numbers. We can rewrite 4 as (2i)², where i is the imaginary unit (√-1). Then our expression becomes:
x⁵ + (2i)² = x⁵ + (2i)²
Now we can use a more general sum of powers factorization technique, recognizing the pattern of roots of unity. However, a simpler and more intuitive approach involves observing that x⁵ = -4 can be solved using De Moivre's Theorem.
By solving x⁵ = -4, we find the five roots in the complex plane. These roots are evenly spaced around a circle with radius ⁴√4 in the complex plane. These roots provide the foundation for the factorization.
The Role of Complex Numbers: Beyond the Real World
The factorization of x⁵ + 4 necessitates venturing beyond the realm of real numbers and into the world of complex numbers. This is because the equation x⁵ = -4 has complex roots, even though the original expression appears to involve only real numbers. This is a common occurrence in higher-order polynomial equations.
Complex numbers are numbers of the form a + bi, where a and b are real numbers, and i is the imaginary unit (√-1). They are indispensable in many areas of mathematics, including algebra, calculus, and physics. The roots of x⁵ + 4 are found using the polar form of complex numbers and De Moivre's theorem.
De Moivre's Theorem states that for any complex number z = r(cos θ + i sin θ), we have zⁿ = rⁿ(cos nθ + i sin nθ). Using this theorem to solve x⁵ = -4 leads to the five complex roots, which ultimately form the basis for the complete factorization of the polynomial.
The Complete Factorization: A Revealing Result
The complete factorization of x⁵ + 4 involves both real and complex factors. Deriving this factorization requires meticulous calculation using the roots obtained through De Moivre's theorem. The process is intricate and involves converting the roots from polar form to rectangular form (a + bi). The final factorization is a product of a quadratic and three linear factors, all containing complex coefficients.
The result takes the form:
x⁵ + 4 = (x + 2)(x² - 2x + 4)(x² + 2x + 4)
Notice that (x² - 2x + 4) and (x² + 2x + 4) are quadratic polynomials with complex roots. These roots are among the five complex roots of x⁵ + 4 = 0. This complete factorization provides a profound insight into the relationship between the polynomial's coefficients and its roots.
Applications and Further Exploration
While seemingly abstract, the exploration of x⁵ + 4 offers several valuable applications and avenues for further exploration:
-
Abstract Algebra: The factorization of this polynomial can be viewed through the lens of Galois theory, a branch of abstract algebra dealing with the symmetry of polynomial equations. The symmetries in the roots provide insights into the structure of the polynomial's field extensions.
-
Number Theory: Investigating the nature of the roots of x⁵ + 4 can reveal connections to other areas within number theory, particularly the study of algebraic numbers and their properties.
-
Numerical Analysis: Understanding the distribution of the roots in the complex plane is relevant in numerical analysis when dealing with polynomial approximation or root-finding algorithms.
-
Complex Analysis: The complete factorization offers further avenues for exploration within complex analysis. The behavior of the polynomial in the complex plane, including its contour integrals and singularities, can be studied to gain a deeper mathematical understanding.
Frequently Asked Questions (FAQ)
-
Q: Why are complex numbers necessary to factor x⁵ + 4?
A: The equation x⁵ = -4 has five roots, and not all of them are real numbers. The use of complex numbers is essential to find all five roots and achieve the complete factorization.
-
Q: Can this method be generalized to other polynomials of the form xⁿ + aⁿ?
A: Yes, a similar approach using roots of unity and De Moivre's Theorem can be applied to factor polynomials of the form xⁿ + aⁿ, where n is a positive integer, and a is a real or complex number. The complexity increases with higher values of n.
-
Q: What are the practical applications of understanding this factorization?
A: While not immediately obvious, the deeper understanding of polynomial factorization and the use of complex numbers are fundamental in many fields, including engineering, physics, and computer science.
-
Q: Are there alternative methods for factoring x⁵ + 4?
A: While the method using De Moivre's Theorem is elegant, other methods involving polynomial long division and root-finding algorithms exist. However, they might prove to be more laborious.
Conclusion: The Beauty of Mathematical Exploration
The seemingly simple expression x⁵ + 4 leads to a surprisingly rich and insightful journey through the world of mathematics. From the initial struggle to factor it, to the realization of the essential role of complex numbers, the exploration provides a compelling case study for the power of mathematical techniques and the unexpected beauty hidden within even simple-looking algebraic expressions. The complete factorization reveals a deeper structure and connects this seemingly simple expression to powerful concepts in algebra and number theory, illustrating the interconnectedness and elegance of the mathematical world. The exploration of x⁵ + 4 highlights the fact that even seemingly simple problems can open doors to a deeper understanding of the complex and fascinating world of mathematics. It encourages us to continue our pursuit of mathematical knowledge, exploring the intricacies of numbers and their relationships, to unlock new insights and expand our understanding of the universe.
Latest Posts
Latest Posts
-
Painting Gin Lane
Sep 22, 2025
-
16 Of 140
Sep 22, 2025
-
20 Off 72
Sep 22, 2025
-
Working Together 2023
Sep 22, 2025
-
15 Of 600
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 5 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.