15 Of 600
interactiveleap
Sep 22, 2025 · 5 min read
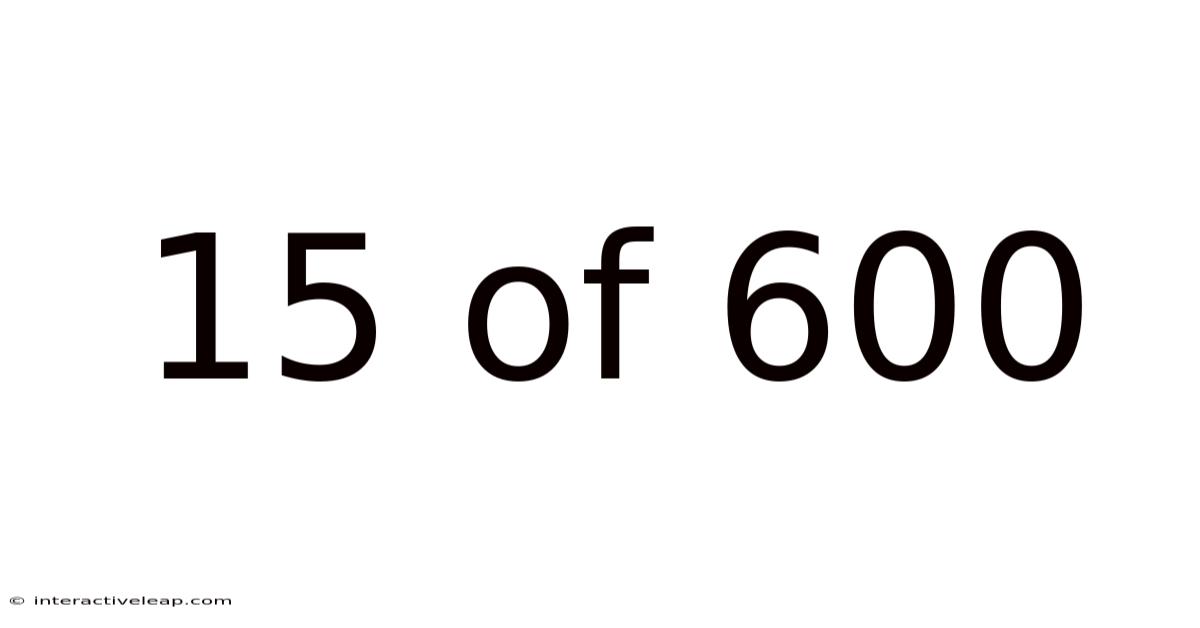
Table of Contents
Unveiling the Mystery: Understanding 15/600 and its Implications
The fraction 15/600, seemingly simple at first glance, opens a door to a world of mathematical concepts and practical applications. This article will delve deep into the meaning and significance of this fraction, exploring its simplification, percentage representation, applications in various fields, and addressing frequently asked questions. Understanding 15/600 can provide a foundational understanding of fractions, ratios, and percentages – essential skills for everyday life and advanced studies.
Introduction: Deconstructing the Fraction 15/600
The fraction 15/600 represents a part-to-whole relationship. It signifies 15 parts out of a total of 600 parts. At its core, it's a ratio – a comparison of two quantities. While seemingly straightforward, exploring this fraction allows us to explore key mathematical concepts and their real-world applications. We will explore simplification, conversion to percentage, and its use in probability, statistics, and other areas.
1. Simplifying the Fraction: Finding the Lowest Terms
Before delving into more complex analyses, it's crucial to simplify the fraction 15/600 to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (600) and dividing both by it.
The GCD of 15 and 600 is 15. Dividing both the numerator and the denominator by 15, we get:
15 ÷ 15 = 1 600 ÷ 15 = 40
Therefore, the simplified form of 15/600 is 1/40. This simplified form is easier to work with and provides a clearer understanding of the proportion.
2. Converting to Percentage: Expressing the Fraction as a Rate
Converting a fraction to a percentage provides a readily understandable representation of the proportion. To convert 1/40 (the simplified form of 15/600) to a percentage, we perform the following calculation:
(1/40) * 100% = 2.5%
Therefore, 15/600 is equivalent to 2.5%. This means that 15 represents 2.5% of the total 600. This percentage representation is often more intuitive and easier to grasp in various real-world scenarios.
3. Applications of 15/600 (or 1/40) in Real-World Scenarios
The fraction 15/600, or its simplified form 1/40, appears in a multitude of real-world situations. Here are a few examples:
-
Probability: Imagine a bag containing 600 marbles, 15 of which are red. The probability of picking a red marble at random is 15/600, or 1/40 (2.5%).
-
Statistics: In a survey of 600 people, 15 responded positively to a specific question. The percentage of positive responses is 2.5%.
-
Finance: If you invest $600 and earn a profit of $15, your return on investment is 2.5%.
-
Measurements: If a length of 600 centimeters is divided into 40 equal parts, each part measures 15 centimeters (1/40 of 600).
-
Manufacturing: If a factory produces 600 units, and 15 are defective, the defect rate is 2.5%.
-
Data Analysis: In a dataset of 600 entries, if 15 meet a specific criterion, the proportion of entries meeting that criterion is 2.5%.
4. Expanding the Understanding: Ratios and Proportions
The fraction 15/600 exemplifies the concept of a ratio, expressing the relationship between two quantities. It can also be understood within the broader context of proportions. A proportion is a statement that two ratios are equal. For example:
15/600 = x/100 (finding what percentage 15 is of 600)
Solving for x, we find x = 2.5, confirming our earlier calculation that 15/600 is 2.5%. Understanding proportions allows us to solve various problems involving scaling, resizing, and similar comparisons.
5. Further Mathematical Explorations: Decimals and Fractions
The fraction 15/600 can also be expressed as a decimal. Dividing 15 by 600 yields 0.025. This decimal representation is another way of expressing the same proportion. Understanding the interplay between fractions and decimals is essential for various mathematical calculations and applications.
6. The Significance of Simplification:
Simplifying fractions like 15/600 to its lowest form, 1/40, is crucial for several reasons:
- Ease of Calculation: Working with smaller numbers makes calculations easier and less prone to errors.
- Clearer Understanding: The simplified fraction provides a more immediate and intuitive understanding of the proportion involved.
- Standardization: Simplifying fractions ensures a consistent and standardized representation of the ratio.
7. Addressing Common Misconceptions
A common misconception is that simplifying a fraction changes its value. This is incorrect. Simplifying a fraction merely changes its representation; the underlying ratio remains unchanged. 15/600 and 1/40 represent the same proportion.
8. Beyond the Basics: Advanced Applications
While the applications above highlight common uses, the principles underlying 15/600 extend to more advanced concepts in:
- Calculus: Derivatives and integrals often involve working with fractions and ratios.
- Linear Algebra: Matrices and vectors use similar principles of ratio and proportion.
- Statistical Modeling: Probability distributions and hypothesis testing heavily rely on understanding proportions and ratios.
9. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 15/600?
- A: The simplest form is 1/40.
-
Q: What is 15/600 as a percentage?
- A: 15/600 is equal to 2.5%.
-
Q: How do I convert 15/600 to a decimal?
- A: Divide 15 by 600, which equals 0.025.
-
Q: What are some real-world examples of using 15/600?
- A: See Section 3 for various examples in probability, statistics, finance, and other fields.
-
Q: Does simplifying a fraction change its value?
- A: No, simplifying a fraction only changes its representation, not its value.
10. Conclusion: The Enduring Importance of Fractions
The seemingly simple fraction 15/600 serves as a powerful illustration of fundamental mathematical concepts. Through simplification, percentage conversion, and exploration of its applications, we've uncovered its importance in diverse fields. Understanding fractions like 15/600 is not merely an academic exercise; it's a crucial skill that empowers us to analyze data, solve problems, and make informed decisions in our daily lives. From probability calculations to financial analysis, the principles embedded within this fraction extend far beyond the classroom, highlighting its enduring relevance and importance. Mastering the manipulation and interpretation of fractions is a cornerstone of mathematical literacy and a valuable asset across numerous disciplines. The ability to easily simplify, convert, and apply fractions like 15/600 is a testament to a strong mathematical foundation.
Latest Posts
Latest Posts
-
5 Of 42
Sep 22, 2025
-
164lbs To Kg
Sep 22, 2025
-
Metallic Hair Dye
Sep 22, 2025
-
Wood Glue Strongest
Sep 22, 2025
-
American Spirit Orange
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 600 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.